К оглавлению

Ускоренный метод вычисления истинной мощности пластов по видимой, замеренной по стволу наклонной скважины

Л.А. БУРЯКОВСКИЙ

Определение истинной мощности пластов по замерам видимой мощности в скважине, искривленной в произвольном направлении, является одной из наиболее частых задач в практике нефтепромысловой геологии. Эта задача решается также при полевой съемке, при послойном описании обнажений, когда приходится иметь дело с замерами мощности в произвольных направлениях по отношению к плоскости падения пласта. Конечной целью вычисления истинных мощностей в скважинах являются построение карт равных мощностей и составление нормального разреза месторождения или разведочной площади.

Однако в практике обработки геологических наблюдений этот вопрос зачастую упрощается во вред точности построения. Наиболее точным является расчет по формуле П.М. Леонтовского [1], которая редко применяется из-за ее громоздкости:

где Т и T_v - соответственно истинная и видимая мощности;-угол падения пластов;- угол отклонения ствола скважины от вертикали;- острый угол между линией падения пласта и горизонтальной проекцией ствола скважины.

Если скважина искривлена вверх по восстанию, то в формуле берется знак плюс, если вниз по падению, то берется знак минус.

Номограмма для ускоренного подсчета по формуле Леонтовского была дана в 1934 г. И.Я. Фурманом [3]. Пользование этой номограммой предусматривает некоторые предварительные выкладки и использование одной подсобной номограммы Т. Смита. При массовости вычислений это создает свои трудности.

Для большей рационализации процесса вычислений нами построены графики, позволяющие вычислить с достаточной точностью истинную мощность пласта по видимой, замеренной по стволу наклонной скважины. При помощи этих графиков вычисляется тригонометрическая часть формулы, которая представляет собой некоторый коэффициент а<= 1, на который надо умножить видимую мощность, чтобы получить значение истинной мощности. Формула П.М. Леонтовского приобретает вид:

Где

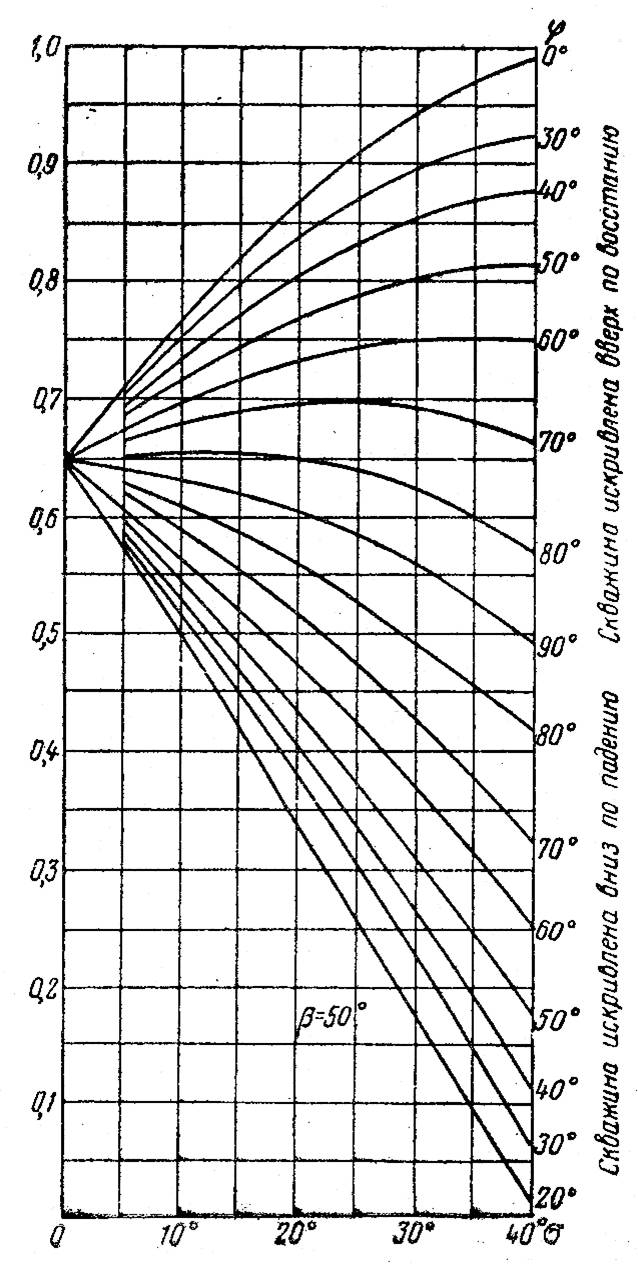
Каждый график рассчитан для одного определенного угла падения b и представляет собой систему линий на плоскости координат  - а. На рис. 1-4 приводятся графики для углов падения b = 20°, 30°, 40° и 50°. Пользование ими несложно. На горизонтальной шкале берется соответствующийотсчет угла искривления скважины  и проводится вертикальный луч до пересечения с одной из линий. Из точки пересечения проводится горизонтальный луч до встречи с вертикальной шкалой, где и прочитывается коэффициент а. Умножая последний на видимую мощность, получаем значение истинной мощности.

Утлылегко получаются графически в результате нанесения инклинограмм скважин на структурные карты как острые углы между азимутом линии падения (или восстания) пластов и азимутом линии отклонения скважины.

Углыберутся из инклинограмм скважин, причем для определенного интервала мощности можно брать средний угол.

Пример. Угол падения пластов b = 30°, азимут падения 210°. Скважина отклонилась от отвеса в интервале замеряемой мощности на 15°, по азимуту 160°. Видимая мощность по стволу скважины Tv = 74 м. Определить истинную мощность.

Пользуемся графиком для b = 30°. Острый угол между азимутами линии падения и линии отклонения= 50°. На горизонтальной шкале берем отсчет= 15°, восстанавливаем перпендикуляр до встречи с линией =50° (скважина искривлена вниз по падению) и проводим горизонтальный луч до шкалы а, где берем отсчет а = 0,75. Истинная мощность равна 74X0,75 = 55,5 м.

Если не учесть уголи подсчитать истинную мощность по упрощенной формуле  то получим T’ = 52,3 м. Абсолютная погрешность D=Т-T’= 55,5-52,3 = 3,2 м. Относительная погрешность=3.2/55.5*100= 5,8%. С увеличением угла погрешность возрастает.

Отсчет а на графиках можно брать с точностью до 1 мм, что дает погрешность в масштабе конечной шкалы а= ± 0,5%, или 0,5 м на 100 м мощности.

Быстрое определение истинной мощности пласта без ограничения величин углов  может быть выполнено также при помощи составной номограммы, сконструированной нами для подсчета коэффициента а при любых углах падения b (0°<b<90°) и углах искривления(0°<<90°).

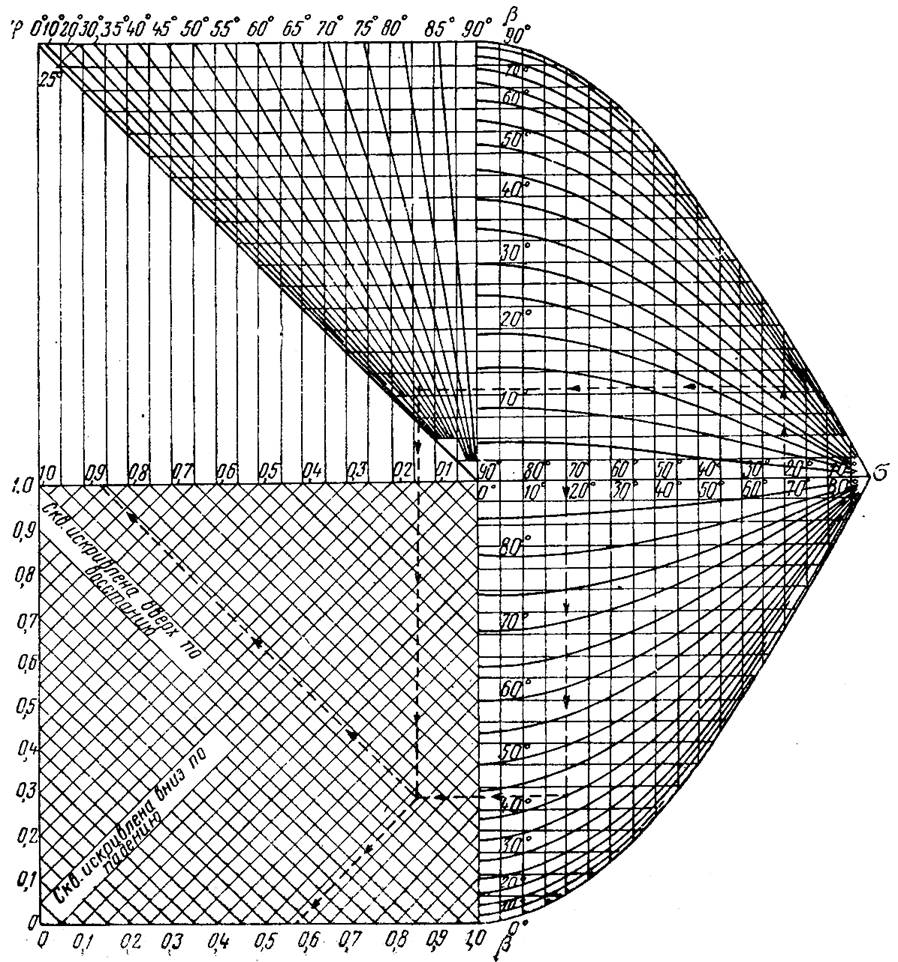
Значения углов  берутся на правой половине горизонтальной оси, и им соответствует ряд вертикальных прямых правой половины номограммы. Углам b соответствуют кривые линии правой половины номограммы, причем возле каждой кривой надписано значение b через 5°. Углам  соответствует пучок прямых в левом верхнем квадрате. Левый нижний квадрат служит для сложения или вычитания элементов  и  в зависимости от пространственного направления искривления скважины.

Пользование номограммой несложно, ключ показан на рис. 5 в виде решения примера для данных  и . Если скважина искривлена вверх по восстанию, то ответ находим на верхней шкале левого нижнего квадрата (а = 0,862); если скважина искривлена вниз по падению, то ответ находим на нижней шкале того же квадрата (а = 0,582) или на левой вертикальной шкале.

Отсчет а по номограмме можно брать с точностью до 1 мм, что дает погрешность в масштабе конечных шкал а= ±1%, или 1 м на 100 м.

Поскольку формула П.М. Леонтовского пригодна и для вычислений в условиях полевой съемки, предлагаемые номограммы могут быть использованы и в этом случае, причем b, как и выше, угол падения,- угол склона,- острый угол между линией падения и линией замера. Обращение с номограммами настолько просто, что работа может быть поручена технику-геологу, коллектору или вычислителю.

ЛИТЕРАТУРА

1. Леонтовский П.М. Практический курс горной геометрии. Гостехиздат, 1924.

2. Мелентьев П.В. Построение номограмм. Гостехиздат, 1930.

3. Фурман И.Я. Геологические построения по данным бурения. Азнефтеиздат, 1948.

НПУ «Гюргяннефть»

Рис. 1.

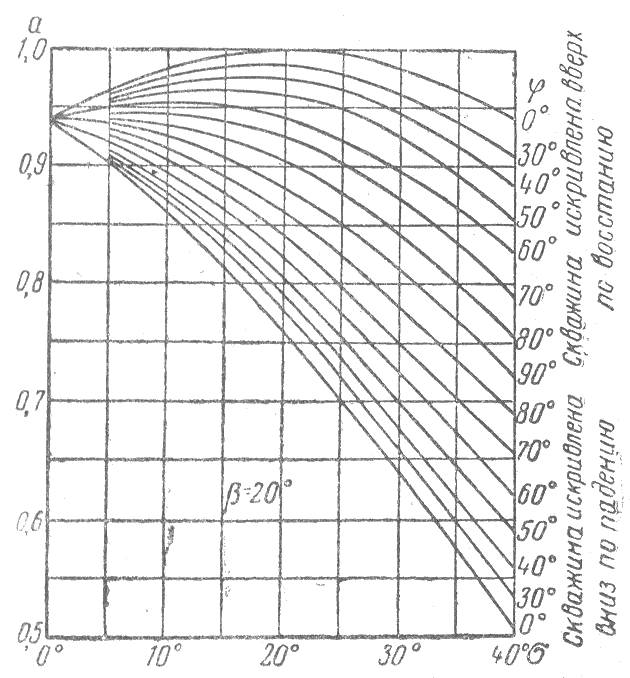
Рис. 2.

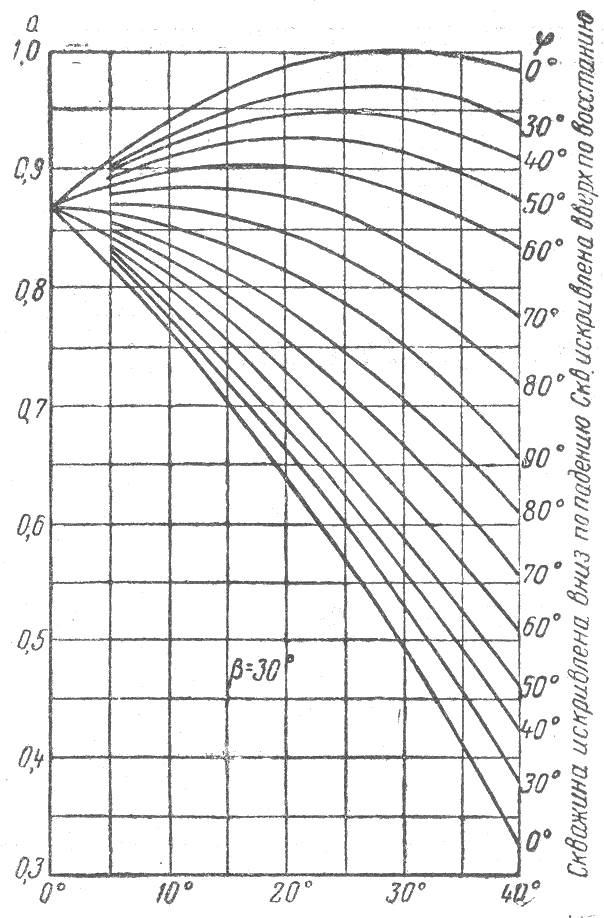
Рис.3.

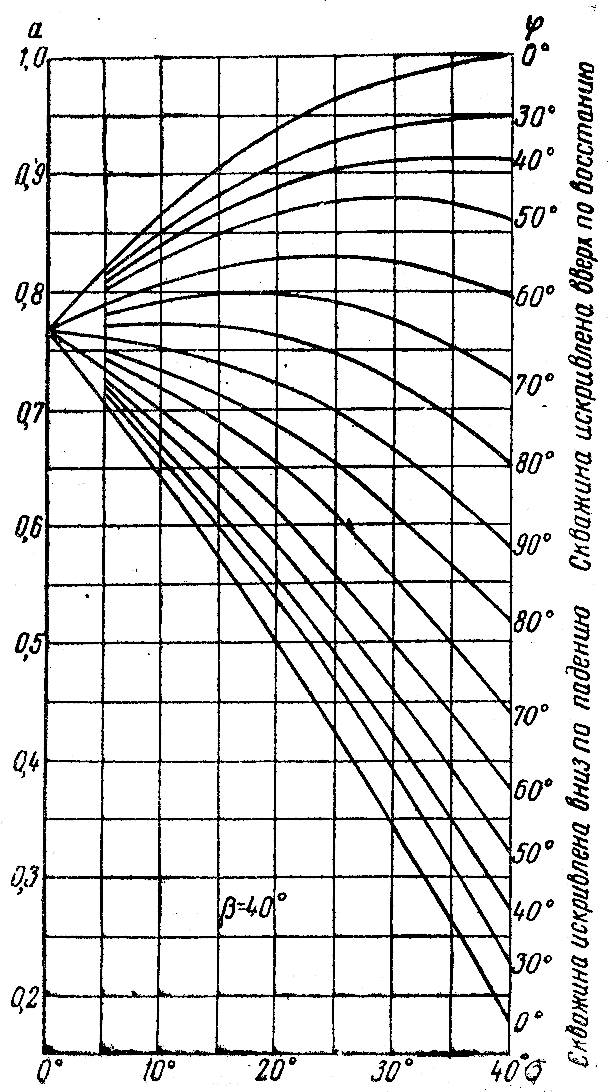
Рис. 4.

Рис.5.