К оглавлению

О зависимости между удельным сопротивлением и коллекторскими свойствами водоносных терригенных пород

А.И. КРИНАРИ

При изучении связи между удельным сопротивлением и коллекторскими свойствами пластов обычно пользуются относительным сопротивлением.

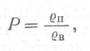
где- удельное сопротивление водоносной породы;-удельное сопротивление насыщающей ее воды.

Проводимые до сих пор исследования посвящены в основном взаимосвязи относительного сопротивления с пористостью, и мало работ о связи этого коэффициента с проницаемостью водоносных пород [3, 10].

Впервые количественная связь между коэффициентом Р и пористостью m была установлена Максвеллом для фиктивного (сложенного идеальными шарами) грунта в следующем виде:

У естественных пород для выражения зависимости Р от m предложен ряд эмпирических формул.

Так, в зарубежной практике широко известны формула Арчи [9].

где q - показатель степени, зависящий от цементации породы, и формула Хамбла

В СССР В.Н. Дахнов [1] предлагает пользоваться формулой вида

где а и b зависят от состава и степени цементации пород. Ф.И. Котяхов [3] рекомендует ту же формулу со значениями а = 0,5035 и b = 2,1; С. Г. Комаров [2] - формулу Арчи; И. Е. Эйдман [8] - видоизмененную формулу Максвелла

где q - коэффициент, зависящий от структуры пород. Г.С. Морозов предлагает аналогичную формулу

Характерной особенностью этих и подобных формул является то, что коэффициент и показатель степени при m являются средними для региона и в каждом конкретном случае от них будут наблюдаться те или иные отклонения. Не лучше будет и в том случае, если принимать в каждом отдельном случае значения коэффициентов и показателя степени, исходя из общих представлений.

Исследования показали, что для песчаников с пористостью 7-29% относительная погрешность в определении пористости по относительному сопротивлению в большинстве случаев составляет 20-44%, т. е. практически определить ее невозможно. От каких же особенностей пород зависит их удельное сопротивление? Для решения этого вопроса были предприняты детальные исследования электропроводности терригенных пород-коллекторов девона Татарии - в комплексе с изучением их литологических (состав, структура, плотность укладки зерен, характер цементации и т. п.) и коллекторских (морфология порового пространства, размер поровых каналов, степень их однородности, пористость и проницаемость) особенностей. Эти исследования, на методике которых мы не останавливаемся, позволили выяснить природу связей между коллекторскими свойствами и коэффициентом Р и выбрать наиболее рациональное направление для его использования.

Относительное сопротивление грунта с прямыми цилиндрическими поровыми каналами, ориентированными по длине объема (идеальный грунт):

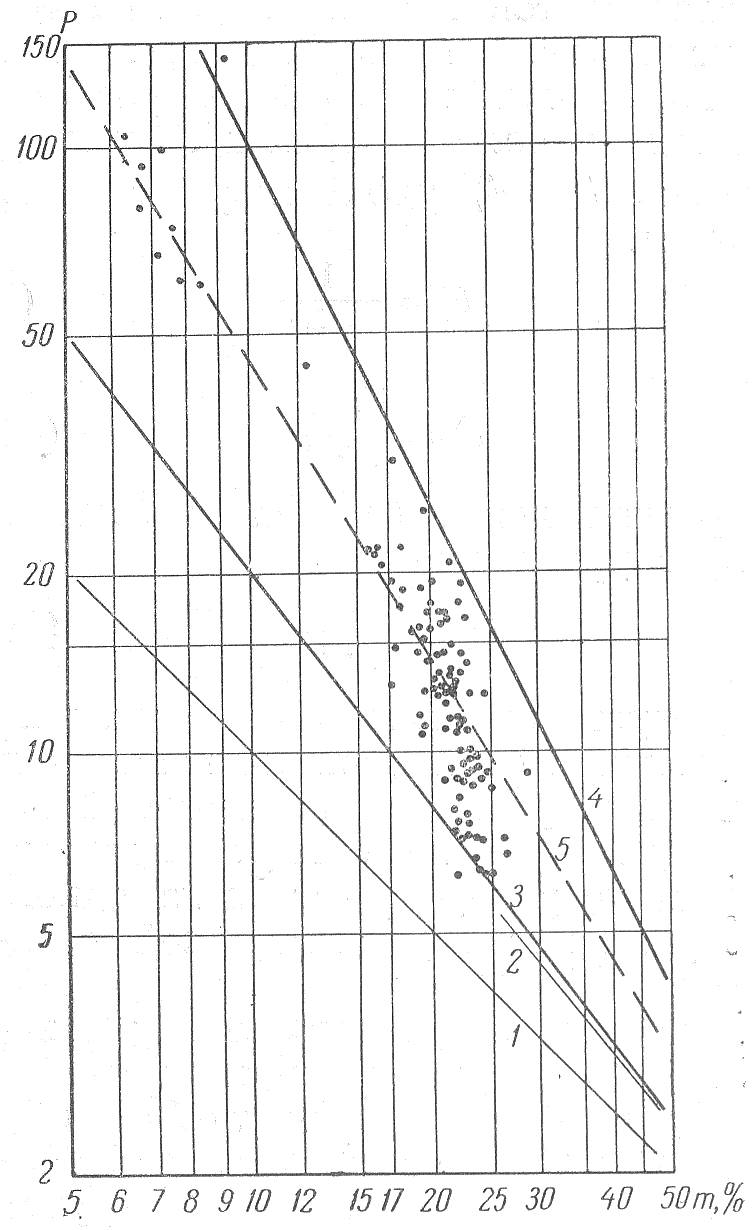
Графически эта зависимость в логарифмической системе координат выражается прямой (рис. 1, линия 1).

Относительное сопротивление фиктивного грунта будет больше относительного сопротивления идеального грунта, так как длина токопроводящих каналов в фиктивном грунте увеличивается за счет извилистости, а «полезная» площадь сечения уменьшается за счет тупиков.

Выше мы отмечали, что зависимость между коэффициентом Р и пористостью для фиктивного грунта удовлетворяет формуле (1). Графически эта зависимость в пределах изменения пористости фиктивного грунта (25,9-47,6) представляет прямую (см. рис. 1, линия 2), уравнение которой

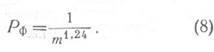
На том же графике точками даны результаты наших определений пористости и коэффициента относительного сопротивления для песчаников и алевролитов пашийской свиты Ромашкинского месторождения. Как видно, точки на графике располагаются в полосе, границы которой (прямые 3 и 4) удовлетворяют уравнениям

 и

а средняя линия (кривая 5) соответствует уравнению

Следует отметить, что согласно полученным нами данным показатель степени в формуле, связывающей величину Р и m, не остается постоянным даже у пород, взятых из одного продуктивного горизонта одной скважины.

В общем зависимость между относительным сопротивлением и пористостью удовлетворяет формуле Арчи (2), в которой значения q для идеального грунта 1,0, для фиктивного грунта 1,24, для естественных пород 1,3-2,0.

Следовательно, относительное сопротивление водоносных пород не имеет прямой связи с пористостью, и определение последней по этому параметру без точных данных о величине показателя степени в каждом конкретном случае не может дать надежных результатов. Решающее значение при этом имеет структура пород (извилистость норовых каналов, тупики и т. п.).

Посмотрим теперь, какова связь относительного сопротивления с проницаемостью водоносных пород.

По Вилли и Валтеру [10] зависимость между относительным сопротивлением и проницаемостью водоносных пород имеет следующий вид (в наших обозначениях):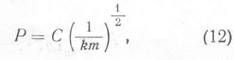

где С - коэффициент, зависящий от межфазового натяжения, давления вытеснения и формы пор, взятый постоянной величиной для данного месторождения; k - коэффициент проницаемости пород.

Влияние формы пор не может быть постоянной величиной. Давление вытеснения имеет тесную связь с диаметрами пор (дисперсностью породы), которые также изменяются в широких пределах. Следовательно, С для наших месторождений не может быть постоянной величиной, а формула (12) обеспечить достаточную точность.

Ф.И. Котяхов [3], используя зависимость между проницаемостью, пористостью и средним радиусом пор r для идеального грунта, с одной стороны, относительным сопротивлением и пористостью, с другой, дает зависимость относительного сопротивления от проницаемости в следующем виде:

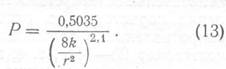
Однако эта формула, основанная на представлениях об идеальной структуре пород, не может быть распространена на природные коллекторы.

Известно, что расход (Q) жидкости через прямую цилиндрическую трубу при ламинарном потоке определяется формулой Пуазейля

где DР - перепад давления на концах трубы; F - площадь поперечного сечения трубы; r - радиус трубы; L - длина трубы; m - вязкость жидкости.

Очевидно, что через идеальный грунт расход будет

а через фиктивный грунт

где r - средний радиус поровых каналов; q₀ - коэффициент, учитывающий структуру порового пространства (извилистость поровых каналов, тупиков и т. п.).

В фиктивном грунте коэффициент, обязанный извилистости поровых каналов, составляет 1,07, а коэффициент, обязанный тупикам, 1,44 [5, стр. 174]. Тогда

Как видно, для фиктивного грунта

и

По-видимому, следует ожидать, что и расход жидкости через естественный зернистый грунт составит (Подмена множителя q₀ в (18) показателем степени q из (2) недостаточно обоснована. Экспериментальное доказательство этого (см. далее) неубедительно ввиду малого диапазона изменения q. - Ред.)

где q - соответствующее этой породе значение показателя степени в уравнении (2) или коэффициент, зависящий от структуры породы.

По закону Дарси скорость фильтрации

Из (18) и (19) получим

Если k выразить в миллидарси, радиус пор заменить их диаметром d и выразить в микронах, а m в процентах, то уравнение (20) примет вид:

Подставляя в (21) значение q из логарифмированного (2), получим

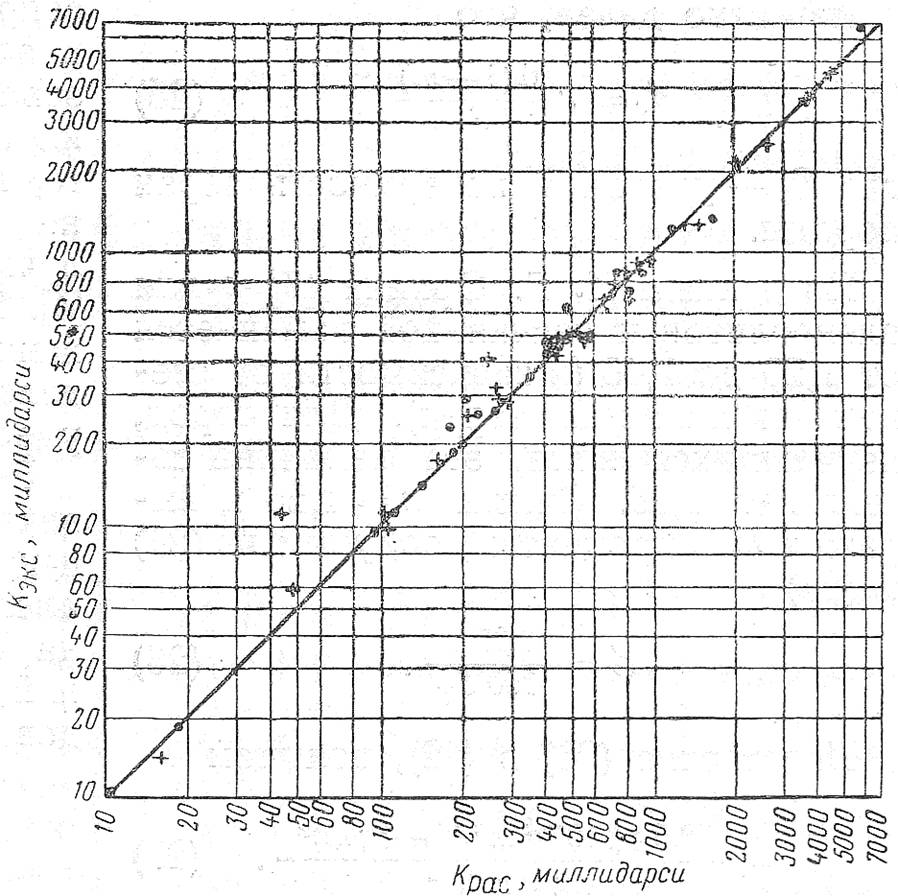
этой формуле для ряда образцов были определены значения проницаемости k_Рас. и сопоставлены со значениями проницаемости k_ЭКc, полученными экспериментальным путем (Величины диаметра поровых каналов снимались с кумулятивных кривых, построенных по данным измерения пор способом капиллярного давления (медианные значения).).

Результаты сопоставления приведены на рис. 2 (точки). Они показывают хорошую сходимость расчетного и экспериментального значений проницаемости и доказывают справедливость допущений при выводе формулы (18) и достаточную точность уравнения (22).

По [5] для фиктивного грунта

где d - гидравлический радиус пор, равный для круглого порового канала d/4; d_э - эффективный диаметр зерен породы.

Очевидно, для естественного грунта

где с - эмпирический коэффициент, учитывающий несовершенство формы зерен по сравнению с шаром.

Известно далее, что

где- удельная поверхность зерен породы.

По данным К.Г. Оркина [7] с для алевролитов и песчаников изменяется от 1,20 до 1,40 (в зависимости от степени окатанности зерен). Для пород, изучавшихся нами, эта величина составляет 1,26. Считая с=1,26 и выражая m в процентах, получим из (24) и (25)

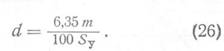
Подставляя (26) в (22), получим

Для проверки этой формулы мы воспользовались данными Ф.И. Котяхова [3, стр. 165], определив по ним расчетные значения проницаемости, которые сопоставили затем с экспериментальными значениями (Обычно считают (для идеального грунта), что при заданной пористости проницаемость обратно пропорциональна квадрату удельной поверхности [3, 7]. Если согласиться с этим, тои k в (27) сокращаются. - Ред.). Полученные результаты приведены на рис. 2 (крестики).

Результаты сопоставлений показали, что средняя относительная погрешность при определении проницаемости по формуле (27) составляет 8,6% (за исключением двух образцов, экспериментальные данные для которых, по-видимому, ошибочны), изменяясь от нуля до 22,4%. Это свидетельствует о достаточной точности уравнения (23) и возможности его практического использования.

На основании проведенных исследований мы считаем, что относительное сопротивление водоносных песчаников и алевролитов целесообразно использовать для бескернового определения их проницаемости. Способов для этого, насколько нам известно, пока еще не разработано. Пористость же их лучше определять по диаграммам ПС [4]. Большое значение в свете изложенного имеют поиски способов определения по каротажным данным удельной поверхности пород.

Безусловно полученные выводы справедливы лишь для пород, аналогичных изучавшимся нами (песчаники и алевролиты терригенной толщи девона Татарии). Для рыхлых образований необходимы специальные исследования.

ЛИТЕРАТУРА

1. Дахнов В.Н. Интерпретация результатов геофизических исследований разрезов скважин. Гостоптехиздат, 1955.

2. Комаров С.Г. Определение пористости пород по удельному сопротивлению. Прикладная геофизика, вып. 14. Гостоптехиздат, 1956.

3. Котяхов Ф.И. Основы физики нефтяного пласта. Гостоптехиздат, 1956.

4. Кринари А.И. Опыт определения пористости пород по каротажным данным. НХ, № 12, 1954.

5. Лейбенезон Л.С. Собрание трудов, т. II. АН СССР, 1953.

6. Морозов Г.С. Метод определения плотности осадочных пород по данным каротажа. Ученые записки Казанского гос. университета, т. 116, кн. 5, 1956.

7. Оркин К.Г. и Кучинский П.К. Физика нефтяного пласта. Гостоптехиздат, 1955

8. Эйдман И.Е. Удельное электрическое сопротивление. Прикладная геофизика, вып. 15, 1956

9. Аrсhiе G.Е. Introduction to Petrophysies of Reservoir Rocks. Bull, of Americ. Ass. of Petr. Geol., v. 34, № 5, 1950.

10. Wyllic M.R.J. and Rose Walter D. Some Theoretical Considerations Related to the Quantitative Evalution of the Physical Characteristies of Reservoir Rock from Electrical Log Dorta, Reprinted from J. Petroleum Technol. Trans. AIME, 189, Apr. 1950.

Казанский филиал АН СССР

Рис. 1.

Рис. 2.