К вопросу упрощения техники подсчета запасов нефти и газа
М.Н. КОЧЕТОВ
При подсчете запасов нефти и газа производятся многочисленные вычисления, связанные с определением средних величин параметров залежи и цифры запасов. В подавляющем большинстве случаев эти вычисления неоправданно громоздки и трудоемки. Цифры запасов нефти и газа, как правило, в отчетах, представляемых на рассмотрение ГКЗ СССР, даются с «точностью» до нескольких тонн или кубометров и даже их долей, несмотря на указание «Инструкции по применению классификации запасов к месторождениям нефти и газов» (Госгеолтехиздат, 1955), что запасы нефти подсчитываются в тысячах тонн, а запасы газа в миллионах кубометров. Подсчет запасов до нескольких тонн или кубометров на самом деле не вносит точности в цифры запасов, а лишь усложняет технику расчета и содержит возможность при оперировании с громоздкими числами грубого просчета, на что указывал А.Л. Козлов [5] еще в 1947 г.
В 1958 г. А.В. Тыжнов [7], рассматривая вопрос упрощения цифрового материала в геологических отчетах и, в частности, при подсчете запасов угля, отмечает, что «запасы даже низших категорий, подсчитываемые на основании сугубо ориентировочных данных, вычисляются иногда с точностью до шестого знака».
Несомненно, упрощение цифрового материала при подсчете запасов любых полезных ископаемых приведет к экономии времени и средств без ущерба точности и достоверности цифр запасов.
Для более или менее обоснованного вывода о необходимости упрощения вычислений при подсчете запасов нефти и газа следует напомнить некоторые сведения из теории ошибок и приближенных вычислений.
В практике подсчета запасов нефти и газа все вычисления производятся с приближенными числами. Приближенные числа получаются в результате счета, округления или измерения, причем при округлении и измерении всегда получаются приближенные числа. Достаточным признаком приближенности результата счета является наличие разных ответов при повторных подсчетах [3].
При округлении точных или приближенных многозначных чисел и десятичных дробей отбрасываемые цифры заменяются нулями. В этом случае, округляя приближенное число, мы вносим к имеющейся погрешности еще погрешность округления. Не рассматривая известные правила округления чисел с избытком или недостатком, напомним лишь правило четной цифры. Так, если отбрасываемое число точно равно половине последнего сохраняемого разряда, то цифру этого разряда оставляют без изменения, если она четная, и увеличивают на единицу, если она нечетная.
При математических операциях с приближенными числами надо учитывать их точность. Так, при сложении и вычитании приближенных чисел в полученном результате нужно отбрасывать по правилам округления цифры тех разрядов справа, которых нет хотя бы в одном из данных приближенных чисел [3]. Конечно, это правило справедливо, если известно, до какой значащей цифры округлено приближенное число, оканчивающееся нулями. Например, при нахождении общей площади нефтеносности, слагающейся из площадей отдельных участков, конечный результат необходимо округлить до разрядов, имеющихся в самом «неточном» числе, подразумевая, что в «неточном» числе нули справа не являются значащими цифрами.
Для пояснения этого приведем пример:
F = f1 +f2+ f3 + f4
где F - общая площадь нефтеносности в га; f1, f2, f3 и f4 - площади нефтеносности отдельных участков залежи в га; f1 = 1200 га; f2 = 134 га; f3 = 37,5 га; f4 = 300 га. Их сумма равна 1671,5 га.
Поскольку слагаемые являются числами приближенными, то и сумма их есть число приближенное, поэтому мы обязаны округлить полученный результат до целых сотен, поскольку в некоторых слагаемых количество десятков, единиц и долей единицы неизвестно. После округления суммарная площадь будет равна 1700 га.
Наглядно результат сложения можно представить, если заменить значком X неизвестное число десятков и единиц в слагаемых. Тогда
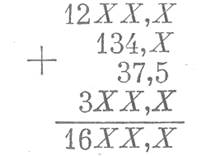
Приняв во внимание известное в сумме число десятков и единиц, получим 1671,5 ~ 1700 га.
Таким образом, принимая во внимание известное число десятков и единиц при сложении и вычитании приближенных чисел, мы полученный результат округляем, заменяя неизвестное число десятков и единиц нулями. В данном случае число округлено до двух значащих цифр. Как известно, значащими цифрами числа являются цифры 1, 2, 3, ... , 9; нуль или несколько нулей считаются значащими цифрами, если они стоят между другими значащими цифрами в числе. Нули же в начале и конце числа считаются незначащими, за исключением случая, когда нуль в конце стоит в том разряде, с точностью до которого взято число, т.е., когда нуль стоит в разряде данной точности [3].
При умножении и делении приближенных чисел в окончательном результате следует также сохранять столько значащих цифр, сколько их имеет приближенный множитель с наименьшим количеством значащих цифр. Например, пусть площадь нефтеносности F = 1700 га, эффективная нефтенасыщенная мощность пласта h = 15,7 м, тогда объем пласта V будет равен
V =F*h=1700*104*15.7 = 26690*104 м3 ≈ 27000*104 м3.
Для наглядности заменим ненадежное число десятков и единиц в величине площади знаком X. Тогда
V = 17XX*104*15.7 = 26XXX*104
или, учитывая известное число сотен и десятков
V≈ 27000*104 м3.
Приведенный случай можно рассматривать и как умножение приближенного числа (1700*104) на точное (15,7), однако и при этом учитывается количество значащих цифр только в приближенном числе, а на количество цифр в точном числе не обращается внимание.
Применяя указанное выше правило, мы получаем результат с достаточной точностью и, кроме того, избавляемся от ненужных цифр, чем рационализируем вычислительный процесс.
Если же производится умножение нескольких приближенных чисел или последовательное деление на несколько делителей, то при округлении результатов промежуточных действий погрешности округления накопляются и могут в итоге оказать заметное влияние на окончательный результат. Однако, как отмечает В.М. Брадис [1], это влияние можно устранить почти целиком, если во всех промежуточных результатах брать на одну цифру больше, чем это рекомендуется правилами. В окончательном результате эта запасная цифра отбрасывается по правилам округления.
В.У. Грибанов [3] дает следующее правило: «При решении задач с приближенными данными нужно в результатах промежуточных действий сохранять на одну цифру больше, чем требуют правила о результатах отдельных действий, причем при определении количества значащих цифр в промежуточных результатах запасные цифры в числах не принимаются во внимание; в окончательном же результате запасная цифра не пишется».
Относительно точности исходных данных при подсчете запасов нефти можно сделать следующие замечания.
Лабораторией маркшейдерии ВНИИ [8, 9] доказано, что среднеквадратическая ошибка определения величины мощности по каротажным диаграммам масштаба 1:500 в одной скважине колеблется в зависимости от количества прослоев (1-5) от ±0,45 до ±1 м. Точность нахождения средневзвешенной величины мощности по карте изопахит составляет примерно ±0,5 м.
Таким образом, в формулу подсчета запасов нефти объемным методом следует подставлять величину мощности, округленную до целых метров.
Точность определения величины пористости единичного образца [4] составляет ±1%, следовательно, и величину пористости следует округлять до целых процентов. То же замечание относится и к коэффициенту нефтенасыщенности.
На конкретных примерах можно показать целесообразность округления приближенных данных при подсчете запасов нефти.
Извлекаемые запасы нефти категорий А2 и В в семилукских отложениях Соколовогорского месторождения [2] были подсчитаны с точностью до десятых долей тонны, в то время как их площадь нефтеносности определена с точностью до 0,1 км2, пористость - до 1% и т. д. Кроме того, при замере величин площади нефтеносности категорий А2 и В были допущены технические ошибки, составляющие 64 и 58% к истинной величине площади.
При подсчете запасов нефти Жирновского месторождения [6] запасы нефти категорий В, С1 и С2 приведены с точностью до сотен тонн, в результате чего операции с громоздкими цифрами привели к техническим ошибкам. Добиваясь такой точности цифр запасов, авторы в то же время грубо округляли исходные данные. Например, средняя пористость второго пласта верхнебашкирского горизонта с 22,7% была произвольно округлена до 20%.
Произведенная оценка точности подсчета запасов нефти [9] первого пласта верхнебашкирского горизонта месторождения показала, что среднеквадратическая ошибка по категории В ±22%, а категории С1 ±25%.
Таким образом, авторы подсчета бесполезно затратили чрезвычайно много труда на операции с громоздкими числами, не добившись при этом, как и следовало ожидать, точности цифр запасов.
Из приведенного краткого изложения сущности точности цифр подсчитываемых запасов нефти видно, что вопросы точности и упрощения подсчета запасов имеют важное значение, так как при их правильном решении повысится производительность труда большого коллектива геологов-нефтяников. По-видимому, назрела необходимость составления соответствующей инструкции по методике и технике подсчета запасов нефти и газа.
ЛИТЕРАТУРА
1. Брадис В.М. Как надо вычислять. Учпедгиз, 1932.
2. Головатая М.Ф. и др. Подсчет запасов нефти и газа в карбонатных коллекторах семилукских отложений Соколовогорского месторождения. Саратов, ВГФ, 1957.
3. Грибанов В.У. Приближенные вычисления в средней школе. Учпедгиз, 1958.
4. Кобранова В.Н., Лепарская Н.Д. Определение физических свойств горных пород. Гостоптехиздат, 1957.
5. Козлов А.Л. Классификация и методика подсчета запасов природных газов. Гостоптехиздат, 1947.
6. Стремский А.Г. и др. Подсчет запасов нефти и газа по Жирновскому месторождению. Жирновск, ВГФ, 1957.
7. Тыжнов А.В. Упрощение цифрового материала в геологических отчетах. Разведка и охрана недр, № 4, 1958.
8. Фролов Е.Ф. Методика геометризации нефтяных месторождений платформенного типа и усовершенствование методики маркшейдерских работ. Отчет по теме 13. Фонды ВНИИ, 1957.
9. Фролов Е.Ф. Усовершенствование методики маркшейдерских работ и горно-геометрических построений в связи с разведкой и рациональной разработкой залежей нефти и газа для месторождений Волго-Уральской нефтеносной области. Отчет по теме 12. Фонды ВНИИ, 1958.
ВНИИ Нефть