К изучению структуры порового пространства
А. Ф. Богомолова, Н. А. Орлова
На процессы фильтрации нефти и воды, а также на диффузию газов в породах существенно влияет структура порового пространства [1, 2, 3-5, 8-11].
Для характеристики геометрии порового пространства обычно пользуются такими интегральными параметрами пород, как пористость, проницаемость, удельная поверхность, а также величиной радиусов пор (среднего и максимального) или кривыми распределения пор по размерам [3, 5-7, 9, 11]. Но интегральные параметры неполностью отражают структурные особенности пород.
Все методы определения радиусов пор (среднего или максимального) и построения кривых распределения пор по размерам основаны на наблюдении какого- либо эффекта или явления в пористой среде; причем считается, что пористая среда представляет собой некоторую систему капиллярных трубок цилиндрической формы. Следовательно, значения радиусов пор, установленные таким образом, являются фиктивными, условными величинами и, очевидно, поэтому при их определении разными методами получаются неодинаковые результаты [3, 5-7, 9, 11].
Распространено мнение о том, что из-за сложности строения порового пространства его невозможно описать математически, используя существующие методы и понятия, п что единственным путем изучения структуры пористых тел является метод схематического представления ее более простыми системами (моделями), поддающимися математическому анализу [6, 11].
В настоящей работе описывается метод геометрического анализа структуры порового пространства пород-коллекторов.
В качестве характеристики этого пространства предлагается дифференциальная функция F(l) распределения расстояний (l) между зернами.
Практически построить кривую распределения можно путем измерения расстояний l между контурами зерен в плоско-параллельных шлифах (Для того чтобы легче отличать поры от зерен, шлифы следует готовить после предварительного насыщения образцов под вакуумом, окрашенным бакелитом, и после затвердевания последнего [1, 2].) под микроскопом или на фотографиях шлифов (рис. 1). Проведя в плоскости сечения шлифа произвольную систему параллельных равноотстоящих друг от друга прямых, по окулярной шкале последовательно измеряют расстояния между контурами зерен вдоль этих линий (на рис. 1 измеряемые отрезки обозначены прямыми линиями). При этом плотность расположения линий не имеет значения, так как точность кривой распределения будет зависеть лишь от общего числа замеров. Для простоты обработки результатов измерения не записывают величину каждого измеренного отрезка, а лишь фиксируют факт попадания ее в один из выбранных интервалов значений l1-l0; l2-l1; ... lk-lk-1, на которые разбивается весь диапазон изменения l.
Для дальнейшей обработки полученных данных строится ортогональная сетка со шкалами: по оси х = l (одно деление = Dl = одному делению окулярной шкалы микроскопа), по оси у = Vi (vi - количество значений li, приходящихся на i-тый интервал) одно деление = 10 замерам. Результаты каждого замера, выраженные в делениях окулярной шкалы, фиксируются в соответствующем квадрате в виде черточки, как это показано на рис. 2. Равенство измеренного отрезка целому числу делений окулярной шкалы отмечается в квадрате слева от этого числа на оси х.
Таким образом, по мере измерения постепенно строится
гистограмма в координатах Vi = f1
(l), которую затем нетрудно перестроить в координатах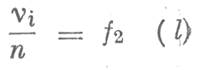 
или 
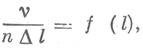, где n = Svi.
Кривая, проведенная через вершины прямоугольников
гистограммы 
, и является статистической кривой
распределения (см. рис. 2).
Статистическая кривая распределения, построенная на основании этих измерений, для однородного изотропного тела, очевидно, будет выражать закон распределения расстояний между зернами во Всем теле. Это следует из того, что в однородном изотропном теле все направления равнозначны. Причем точность получаемого закона распределения будет зависеть, как уже отмечалось, лишь от общего числа измерений. Для анизотропных пористых сред необходимо построить кривые распределения расстояний между зернами соответственно осям анизотропии.
Пользуясь изложенной выше методикой, были построены
гистограммы и статистические кривые распределения (В данном случае кривые строились в координатах
, так как почти все измерения производились при одинаковых или близких значениях Dl.) расстояний между зернами для образцов песчаников,
взятых из продуктивных горизонтов нефтяных месторождений. При этом было
установлено, что для получения воспроизводимых результатов вполне достаточно
сделать около 1000 замеров на одном шлифе. Дальнейшее увеличение количества
замеров не уточняет и не изменяет характера статистической кривой распределения
расстояний между зернами.
Поэтому линии, вдоль которых измеряются расстояния между зернами, надо располагать так, чтобы они пересекли всю площадь шлифа и получить при этом порядка 1000 значений величины l. На основании таких данных определялись наиболее существенные характеристики функции распределения, выражаемые числовыми параметрами:
средним арифметическим 
наиболее вероятным lт и
максимальным - L значениями расстояний между зернами, а также
дисперсией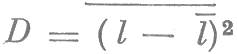 
Указанные параметры, определенные для разных шлифов одного и того же образца породы при различной цене деления окулярной шкалы микроскопа, совпадали в пределах ошибки измерения, равной ± 0,5 деления окулярной шкалы.
По существу эти параметры и надо рассматривать как структурные параметры пористых тел.
В качестве примера на рис. 3 приведены статистические кривые распределения с максимальными и минимальными значениями дисперсии D.
Сравнение полученных данных показывает, что
дифференциальные кривые распределения F(l) и наиболее существенные их параметры 
позволяют составить представление о геометрии порового пространства.
При этом меньшему значению дисперсии D кривых соответствует более однородная структура пор.
Интересно сопоставить кривые распределения расстояний между зернами F (l) с кривыми распределения пор по радиусам, рассчитанным на основании эмпирической зависимости между остаточной водонасыщенностью керна и капиллярным давлением [8]. Такое сопоставление показало хорошую корреляцию максимумов обеих кривых (рис. 4). Однако характер обеих кривых существенно различен. Если наиболее вероятный радиус пор, определенный методом капиллярного вытеснения, совпадает с наиболее вероятным расстоянием между стенками пор, то максимальная величина радиуса пор (~ 25 мк) значительно меньше максимального расстояния между стенками пор, равного в данном примере ~152 мк. Таким образом, предлагаемый статистический метод анализа геометрии порового пространства пород-коллекторов позволяет количественно характеризовать структуру пор.
ЛИТЕРАТУРА
1. Авдусин П.П., Цветкова М.А. ДАН СССР XLI, № 2, 79, 1943; НХ № 6, стр. 24, 1938; ДАН СССР VII, № 9, стр. 943, 1947, ДАН СССР, XX, № 2- 3, стр. 163, 1938.
2. Авдусин П.П. Труды совещания по развитию научно-исследовательских работ в области вторичных методов добычи нефти. Стр. 202, Баку, 1953, Изв. АН АзССР, вып. II, № 6, 1947.
3. Колганов В.И. Об изучении и классификации коллекторов, «Геология нефти», 1957, № 2, стр. 36.
4. Лыков А.В. Явления переноса в капиллярно-пористых телах. Гос. изд. ВСХН, теор. литер., 1954.
5. Методы исследования структуры высокодисперсных и пористых тел. Труды совещания. Июнь, 1951, (1953). Стр. 47, 59, 203, 259, 267.
6. Оркин К.Г., Кучинский П.К. Лабораторные работы по курсу «Физика нефтяного пласта». Гостоптехиздат, стр.169, 1953.
7. Плющ А.М. Труды Нефт. Эксп. АН АзССР, т. III, Баку, 1955.
8. Фигуровский Н.А. Зав. лаб. 15, № 4, стр. 423, 1949, Физическая химия, № 12, стр. 619, 1938.
9. Xанин А.А. «Разведка и охрана недр», № 1, стр. 7, 1956.
10. Электрокинетические свойства капиллярных систем. Монографический сборник. Изд. АН СССР, 1956.
11. Scheidegger A.Е. Annual Mie- ting, Petroleum and natural Gas Division Calgary may, 1958.
ИГ и РГИ
Рис. 1. Измерение расстояний между зернами в шлифе при помощи окулярной шкалы микроскопа.
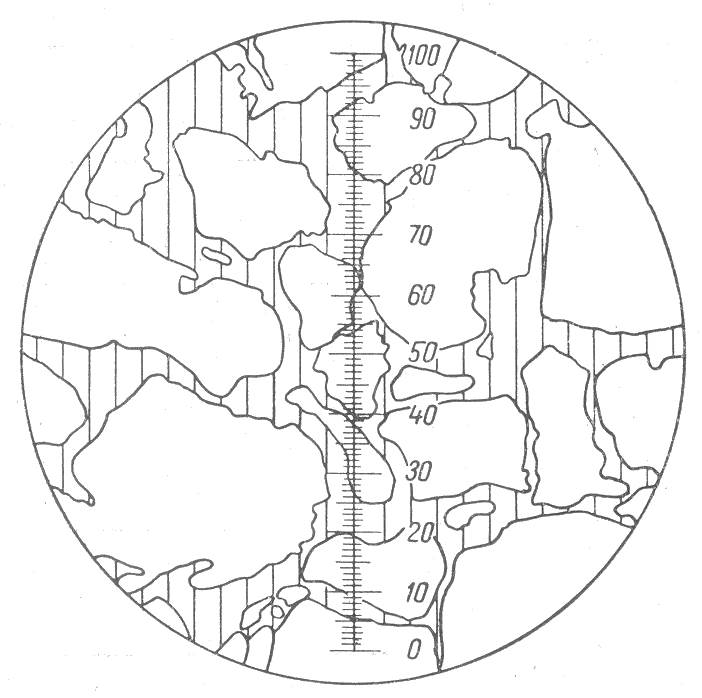
Рис. 2. Построение статической кривой распределения расстояний между зернами.
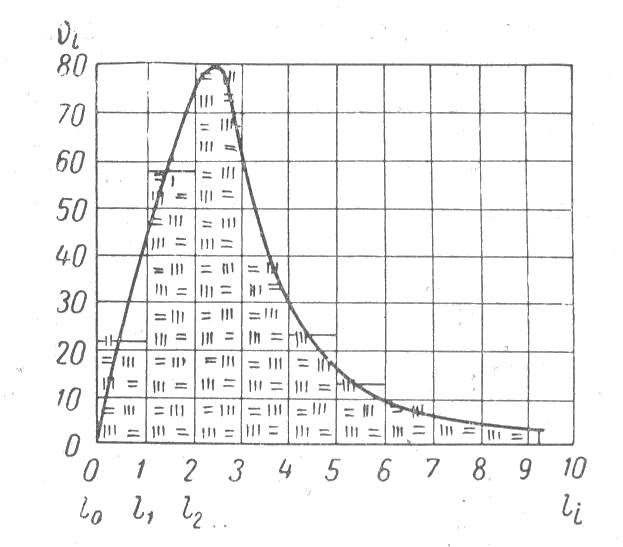
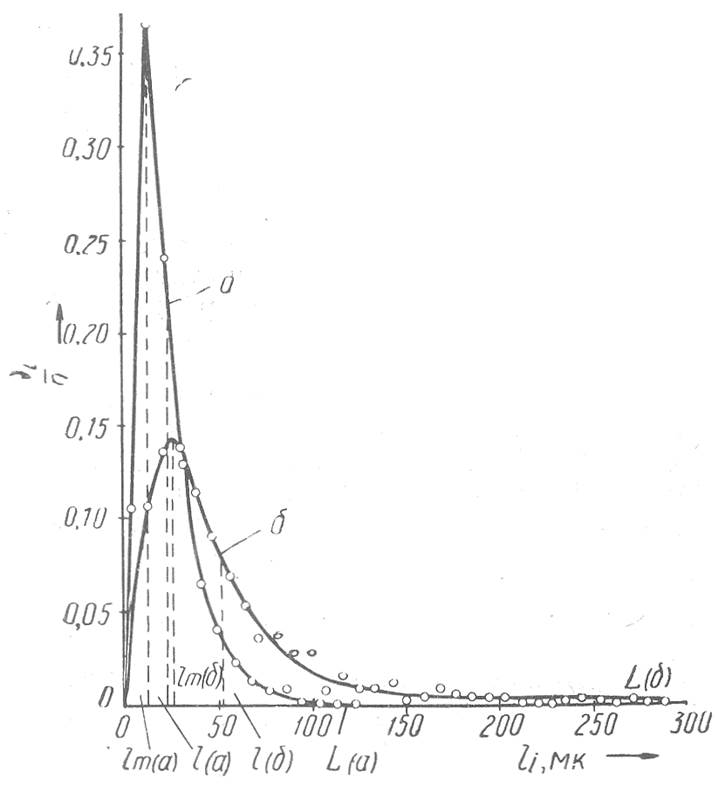
Рис. 4. Сопоставление кривых распределения расстояния между зернами с кривыми распределения пор по радиусам (m = 20%, k = 0,422 дарси).
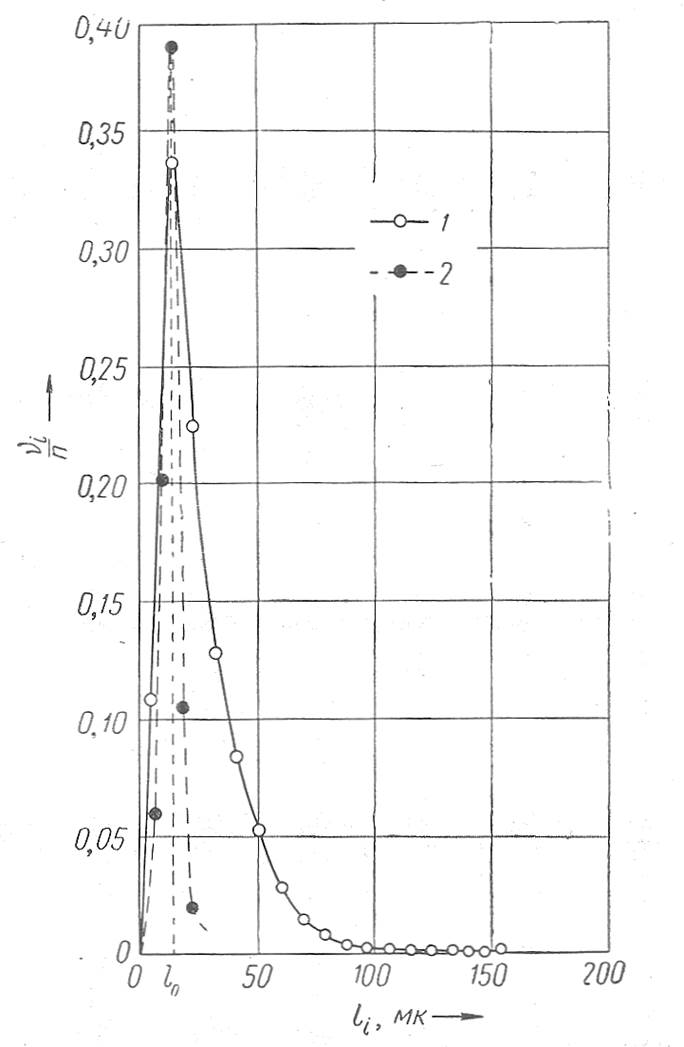
1 - дифференциальная кривая распределения расстояний между зернами; 2 - то же радиусов пор; кривая построена на основании зависимости капиллярного давления от водонасыщенности.