Об определении коэффициента трещиноватости пород по кривым восстановления давления в скважинах
Ф.И. Котяхов
При исследовании трещиноватого коллектора представляют интерес определения коэффициента проницаемости Кт, обусловленного наличием трещин в породе, коэффициента трещиноватости mт и высоты (раскрытости) трещин b.
Рассмотрим возможность определения этих параметров по кривым восстановления давления. При совершенной скважине, когда имеется возможность точно определить ее радиус Rc, для оценки гидродинамических характеристик трещиноватого пласта, в котором жидкость движется только по трещинам, можно воспользоваться следующей формулой:
![]()
где DРc - изменение забойного давления в возмущающей скважине, ат; Q - установившийся дебит на забое скважины к моменту ее остановки или пуска в эксплуатацию, см3/сек; m - вязкость жидкости, сп; Кт - коэффициент проницаемости пласта, обусловленный трещиноватостью пород, дарси; h - мощность пласта, см; c - коэффициент пьезопроводности, см3/сек; t - время с момента остановки или пуска скважины в эксплуатацию, сек; Rc - радиус скважины, см.
Формулу (1) можно представить также в виде
![]()
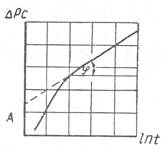
Из формул (1) и (2) легко видеть, что изменение забойного давления в возмущающей скважине является линейной функцией логарифма времени t. Следовательно, если в прямоугольной системе координат по оси ординат откладывать забойное давление Рс или DРс, а по оси абсцисс - логарифм времени, то на графике функциональная зависимость DРс = f (ln t) изобразится прямой, секущей ось ординат на высоте А (см. рисунок). Уклон i прямолинейного участка кривой, т.е. тангенс угла наклона j к оси абсцисс, согласно формуле (2), равен
![]()
Определив по графику i и зная остальные параметры, входящие в формулу (3), можно найти кт:
![]()
Отрезок А, отсекаемый на ординате продолжением прямолинейного участка преобразованной кривой восстановления давления, согласно формуле (2), определится из выражения:
![]()
Отсюда будем иметь
![]()
Решая (6) относительно c, получим
![]()
При несовершенной скважине указанные выше параметры удобнее всего определить по методу (Борисов Ю.П., Васильевский В.Н. Состояние промысловых исследовательских работ и пути их улучшения. Опыт разработки нефтяных месторождений. Труды Всесоюзного совещания работников по добыче нефти, состоявшегося в г. Куйбышеве в 1956 г., Гостоптехиздат, 1957), основанному на том, что в логарифмических координатах все кривые восстановления давления одинаковы и в зависимости от Ктh/m, c, Q и r (расстояния между возмущающей скважиной и скважиной-приемником) смещаются вдоль осей координат в ту или иную сторону. Изменение параметров c и r при прочих равных условиях приводит к перемещению кривой параллельно самой себе вдоль оси абсциссе (lg t). Изменение кт h/m и Q приводит к подобному же смещению вдоль оси ординат.
Поэтому достаточно иметь одну эталонную кривую для единичных параметров Q, r, c и кт h/m. Накладывая ее на фактическую кривую, построенную в том же масштабе и в тех же координатах, определяют смещение кривой по оси абсцисс a и смещение ее по оси ординат b, а затем по величине этих смещений определяют c и ктh/m между двумя скважинами.
![]()
где c0, r0, Кт0, h0, m0, Q0 - параметры, по которым построена эталонная кривая по формуле
![]()
Здесь DРс - изменение забойного давления в скважине-приемнике за время t, ат; Q - дебит возмущающей скважины до остановки или до пуска ее в эксплуатацию, см3/сек; r - расстояние между скважинами, см; остальные обозначения те же, что и в предыдущих формулах.
Определив тем или иным из изложенных методов c и Кт, можно определить коэффициент упругоемкости пласта из выражения
![]()
Применительно к пористым пластам коэффициент упругоемкости пласта b* можно представить также в виде
![]()
где bж - коэффициент сжимаемости жидкости, 1/ат; bс - коэффициент сжимаемости породы, представляющий собой отношение объема пор к объему породы при изменении давления на 1 ат, 1/ат; m - коэффициент полной пористости пласта.
Для трещиноватых коллекторов, из которых жидкость к скважинам поступает исключительно по трещинам, формула (11) не применима, так как сжимаемость пласта в этом случае будет обуславливаться главным образом трещиноватостью породы. Коэффициент сжимаемости породы здесь будет равен
![]()
где DVп и DVт -приращения объемов пор и трещин при изменении давления на 1 ат; V - объем породы.
Иначе говоря, в этом случае коэффициент сжимаемости породы будет определяться коэффициентом сжимаемости, обусловленным наличием в породе пор, т. е.
![]() ,
,
и коэффициентом сжимаемости за счет трещин ![]()
![]()
Напомним, что коэффициент трещиноватости mТ равен mT=VT/V. Следовательно, bТ можно представить также в виде
![]()
где VT - объем трещин.
Таким образом, коэффициент сжимаемости скелета пласта в рассматриваемом случае будет определяться из выражения
![]()
где![]() - коэффициент сжимаемости трещин, равный DVT/VT DР.
- коэффициент сжимаемости трещин, равный DVT/VT DР.
Поскольку жидкость содержится не только в трещинах, но и в порах, то первое слагаемое формулы (11) должно быть равно bж(m+mт).
Следовательно, коэффициент упругоемкости пласта применительно к трещиноватому коллектору равен
![]()
Решая уравнение (15) относительно mТ будем иметь
![]()
Строго говоря, если в порах пласта, по которым не движется жидкость, содержится нефть и вода, а в трещинах только нефть, то член mbЖ должен иметь следующий вид:
![]()
Тогда формула (16) примет вид:
![]()
где a - коэффициент водонасыщенности, доли единицы; bн и bв - соответственно коэффициенты сжимаемости нефти и воды, 1/ат.
Коэффициент упругоемкости пласта b* определяется по формуле (10) изложенными выше способами; m, bН, bв и b - путем соответствующих лабораторных исследований пластовых жидкостей и кернов пористой части коллектора. Таким образом, для определения mт по формуле (16) или (17) необходимо изыскать пути определения коэффициента сжимаемости трещин bт'.
Из изложенного выше видно, что bт' определяется степенью изменения объема трещин при изменении пластового давления на 1 ат.
Такое изменение объема трещин в пласте должно отразиться на форме индикаторных кривых, получаемых при исследовании эксплуатационных и нагнетательных скважин. В эксплуатационных скважинах с увеличением депрессии объем трещин должен уменьшаться, в связи с чем индикаторная кривая будет выпуклой по направлению к оси дебитов. В нагнетательных скважинах будет наблюдаться обратный процесс, и индикаторная кривая примет вогнутую форму. Это подтверждается результатами исследований работы нагнетательных скважин, проведенных Ф. С. Абдулиным на Туймазинском месторождении (Абдулин Ф.С. Расслоение пород девонского продуктивного пласта при законтурном заводнении. Нефт. хоз., 1, 1958.), которые показали, что по мере увеличения давления нагнетания индикаторные кривые приобретают вогнутую форму.
В связи с изложенным важно выяснить, за счет изменения каких габаритных размеров трещин увеличивается или уменьшается их объем при изменении давления в пласте. Из всех размеров трещин, т. е. длины l, ширины а и высоты b наибольшее влияние на расход жидкости в них оказывает высота (раскрытость) b. Как известно, расход жидкости в прямоугольной трещине прямо пропорционален ее ширине, кубу высоты и обратно пропорционален ее длине.
Таким образом, даже при одинаковой относительной деформации трещин, вызванной изменением давления в пласте, преобладающее влияние на расход жидкости в них должно оказывать изменение их высоты. В действительности степень влияния давления в пласте на изменение габаритных размеров трещин не одинакова; наиболее изменчива их высота. Это также подтверждается упомянутыми выше исследованиями Ф. С. Абдулина, который установил, что после нагнетания песка в пласт под давлением изменение последнего не меняет коэффициента приемистости нагнетательных скважин, так как сжатию трещин при понижении давления препятствовал находящийся в них песок. Согласно этому коэффициент сжимаемости трещин можно приближенно рассматривать как
![]()
Учитывая описанное обстоятельство, следует попытаться определить коэффициент сжимаемости трещин bт' по результатам исследований скважин при установившихся отборах жидкости из пласта или при нагнетании ее в пласт. Такой путь, по-видимому, более реален, чем путь лабораторных исследований, хотя и не исключает целесообразность последних.
Как известно (К о т я х о в Ф.И. Основы физики нефтяного пласта. Гостоптехиздат, 1956.)
![]()
где кт-в дарси; b-в см.
![]()
где S - коэффициент густоты трещин, 1/см; F - поверхность фильтрации пласта, см2; l, а, b - соответственно длина, ширина и высота трещин, см; n - число трещин.
С учетом формулы (19), формулу (18) можно представить в следующем виде:
![]()
Отсюда
![]()
При изменении высоты трещины будем иметь b' и проницаемость пласта, обусловленную трещиноватостью, кт'. Тогда формула (21) примет вид:
![]()
Пользуясь формулами (21) и (21 *), получим формулу для определения bт':
![]()
Принимая во внимание прямую зависимость между продуктивностью скважин и проницаемостью пласта, формулу (22) можно представить также в виде
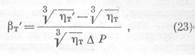
где hт и hт' – коэффициенты (hт определяется по прямолинейному участку индикаторной прямой.) приемистости нагнетательной скважины до и после изменения давления в пласте на величину DР. Для эксплуатационной скважины эти обозначения соответствуют коэффициентам продуктивности hт' - до изменения давления в пласте и hт - после его изменения, а в знаменателе формулы: (23) должно стоять hт' (В этом случае по прямолинейному участку индикаторной кривой определяется hт').
Подставляя в формулу (16) или (17) величину bт', найденную по формуле (23), определим коэффициент трещиноватости пласта mт в районе исследуемой скважины.
После этого, рассчитав по коэффициентам продуктивности скважин проницаемость пласта, обусловленную его трещиноватостью, можно определить среднюю высоту трещин и по формуле (18) и коэффициент их густоты S по формуле (19).
Таким образом, изложенные выше соображения доказывают принципиальную возможность определения коэффициента трещиноватости пород по кривым восстановления давления в скважинах без помощи глубинного фотографирования.
Следует ожидать, что коэффициент сжимаемости трещин bт' будет зависеть от давления, а следовательно, и от DР. Возможно, что иногда он будет равен нулю. Поэтому исследование его величины при различных давлениях в пласте представляет несомненный интерес.
Изложенное выше, по-видимому, с некоторым приближением можно отнести и к залежам, в которых жидкости движутся не только по трещинам, но и по порам. Так, например, параметры, входящие в формулы (15), (16), (17) и (21), сохраняют свое значение и во втором; случае, исключая проницаемость и пьезопроводность, которые будут обуславливаться наличием в породе не только трещин, но и пор.
Если по результатам анализа кернов известна проницаемость пористой части пласта кп, а по преобразованным кривым восстановления давления известна суммарная проницаемость пласта кс, то проницаемость пласта, обусловленная трещиноватостью кт, определится как разность
![]()
Зная Кт из (24) и mт из (16) или (17), из формулы (18) можно найти среднюю высоту трещин b.
Учитывая изложенное, а также формулу (10), коэффициент пьезопроводности cт, обусловленный трещиноватостью, находим из выражения
![]()
где cс - пьезопроводность пласта, обусловленная совместной работой трещин и пор (Точность определения c и kh/m рассматриваемом случае такая же, как и в гидродинамических расчетах, производимых при проектировании разработки нефтяных залежей.).
В заключение заметим, что нами был определен коэффициент сжимаемости трещин bт' по промысловым данным по изложенной выше методике. Для этого были использованы полученные Ф.С. Абдулиным результаты гидродинамических исследований туймазинских скв. 11, 514 и 540, вскрывших пористо-трещиноватую часть пласта Д1. По ним имелись кривые восстановления давления, индикаторные кривые и проницаемость пласта по кернам.
При помощи формул (3) и (4) по кривым восстановления давления была установлена проницаемость удаленной части пласта, обусловленная наличием в пласте пор и трещин (кс). Затем по величине кс и проницаемости кернов кп по формуле (24) находилась проницаемость пласта кт, обусловленная наличием в нем трещин.
Имея в виду, что
![]()
где hс - суммарный коэффициент продуктивности на прямолинейном участке индикаторной кривой, обусловленный наличием в пласте пор и трещин, из равенства (26) для прямолинейного участка индикаторной кривой можно найти коэффициент продуктивности hс, обусловленный наличием в пласте трещин.
Индикаторные кривые для указанных нагнетательных скважин были вогнутыми к оси дебитов, т. е. по мере увеличения перепада давления на устье скважин коэффициент продуктивности их возрастал. Для каждой точки криволинейного участка индикаторной кривой определялось из разности следующих величин hт`
![]()
где hс' - суммарный коэффициент продуктивности на криволинейном участке индикаторной кривой, обусловленный наличием в пласте пор и трещин; hп - коэффициент продуктивности, обусловленный наличием в пласте пор, который на всех участках индикаторной кривой принимался практически постоянным.
После определения таким путем hт и hт' по формуле (23) подсчитывался коэффициент сжимаемости трещин bт'. При этом DР принималось как разность между давлениями, соответствующими началу криволинейного участка индикаторной кривой и исследуемой точке на ней - hт'.
В итоге таких расчетов было впервые обнаружено, что для скв. 514 bт'=3,8*10-2, для скв. 11 bт' = 1,2*10-2 и для скв. 540 bт' = 4,4*10-2. Далее было установлено, что bт' по этим скважинам не зависит от DР.
Приведенные данные представляют большой интерес, так как показывают, что коэффициент сжимаемости трещин на три порядка больше, чем для жидкостей и пористой среды, и поэтому должен учитываться при исследовании не только чисто трещиноватых, но и пористо-трещиноватых коллекторов. Кроме того, они свидетельствуют о принципиальной возможности и целесообразности определения bт' по промысловым данным.
Коэффициент трещиноватости mт по этим данным определить не удалось, так как исследование скважин основывалось на самопрослушивании, которое при их гидродинамическом несовершенстве недостаточно для определения коэффициента пьезопроводности cт по изложенной выше методике.
Поэтому окончательное решение вопроса о практическом использовании рассмотренного метода, разумеется, должно быть принято после его тщательной проверки в промысловых условиях.
ВНИИнефтъ