О точности определения проницаемости коллекторов по керну
А.И. СОЛОМАСОВ
В настоящее время существует несколько методов определения коэффициента ироницаемости - геофизические, гидродинамические и непосредственно по керну. Данные непосредственных измерений по керну используются для получения номограмм, лежащих в основе геофизических методов определения проницаемости, и применяются для проверки этих методов. Точность определения средней проницаемости по разрезу зависит от количества образцов [1, 2]. Более обстоятельно этот вопрос рассмотрен М.М. Саттаровым [3], который теоретически рассчитал распределение проницаемости для упрощенной модели коллектора. Ниже рассматривается метод оценки точности определения проницаемости по керну, основанный на экспериментальных данных о распределении проницаемости.
Девонские терригенные коллекторы Башкирии и Татарии наиболее однородны по сравнению с коллекторами многих других нефтяных районов страны. Коллекторы здесь сложены мелкозернистыми песчаниками и по электрическим свойствам однородны. Однако их проницаемость изменяется по разрезу в широких пределах. Объясняется это тем, что проницаемость определяется такими тонкими элементами структуры коллектора, которые заметно не отражаются на данных электрического сопротивления и на петрографической характеристике пород. Поэтому проницаемость определяется как средняя арифметическая или средняя взвешенная величина.
Оценка ошибки определения среднего значения проницаемости возможна по теории вероятностей. Для выяснения этой ошибки необходимо знать закон распределения значений проницаемости, но до его нахождения нужно рассмотреть вопрос о возможных систематических погрешностях, возникающих при работе с керновым материалом.
Распространено мнение о том, что в процессе бурения наверх выносятся наиболее плотные (а, следовательно, и менее проницаемые) разности коллекторов. Однако на вынос керна песчаников влияет ряд факторов - давление на забой, скорость вращения и тип долота, величина интервала бурения и т.п. Сопоставление средней проницаемости в интервале долбления с выносом керна свидетельствует об отсутствии связи между этими величинами.
В результате анализа керновых данных о проницаемости установлено, что ее распределение в петрографически и электрически однородных интервалах аппроксимируется законом Пуассона с непрерывной переменной [4, 5],
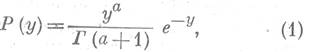
где Р (у) - плотность распределения у;
- нормированное значение Кпр.i,
- постоянная величина.
(
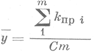- среднее нормированное значение
коэффициента проницаемости ) .
Нормировочный множитель
(2)
где 
- дисперсия
коэффициента проницаемости. Ее значение находится по рис. 1, в.
На рис. 1 в качестве примера приведено сопоставление эмпирического распределения с распределением, рассчитанным по формуле Пуассона. Наблюдающиеся расхождения несущественны и можно утверждать, что распределение проницаемости по разрезу с достаточным приближением подчинено закону Пуассона.
На рис. 1, г изображено распределение средних значений проницаемости по 145 пересечениям, равномерно рассеянным по площади нефтеносной части горизонта ДI Туймазинского месторождения, Сопоставление этого распределения с расчетным также свидетельствует о его соответствии закону Пуассона.
Пользуясь известными [4, 5] свойствами распределения (по Пуассону), можно рассчитать ошибку оценки средней проницаемости по ограниченному числу образцов.
Допустим, что в пределах пластового пересечения имеется т образцов с известной проницаемостью Кпр1, Кпр2,...Кпрm. Каждое нормированное значение указанных величин распределено по закону Пуассона. Пусть эти распределения имеют коэффициенты а1, а2, ..., аm. Тогда на основании теоремы сложения величина
также распределена по закону Пуассона с коэффициентом
(3)
На практике мы всегда располагаем ограниченным числом
членов совокупности, поэтому можно подсчитать только оценку истинного среднего
(математического ожидания) и с некоторой вероятностью определить предельное
расхождение ε между математическим ожиданием М (r) и его оценкой
. Эту вероятность
обычно обозначают через α:
Вероятность α называется
доверительной; границы
- доверительными границами;
- доверительным интервалом.
Доверительные границы характеризуют точность оценки (выборочного среднего), а доверительная
вероятность- ее надежность.
Верхняя граница
нижняя граница
χ2 определяется не только вероятностью Р, но и числом степеней свободы f, которое в нашем случае (для непрерывной переменной) подсчитывается по формулам для верхней границы
fв=2*Z;
для нижней
fн=2*(Z-1);
Задавшись доверительной вероятностью α=Р2 - Р1 и подсчитав f по таблице значений χP2 находят соответствующие значения χ1-P12 и χ1-P22 . При f> 30 χ2 рассчитывается по известным [5] формулам:
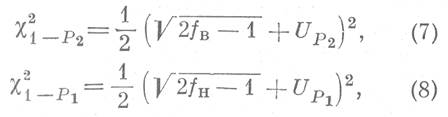
где UP1 и UР2 - квантили нормированного нормального распределения.
По условию 
следовательно,
, тогда с учетом
формул (5) и (6) нижняя и верхняя границы 
для заданной
доверительной вероятности α= Р2 - Р1 соответственно равны:
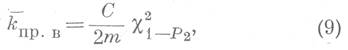
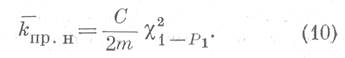
Величины, вычисленные по формулам (9) и (10), позволяют определить с заданной вероятностью предельное отклонение истинного среднего значения проницаемости от выборочного среднего.
Истинное среднее значение проницаемости 
находится в
интервале
Практически известна выборочная средняя проницаемость, а истинная остается неизвестной. Очевидно, что предельная относительная ошибка δ с вероятностью α равна:
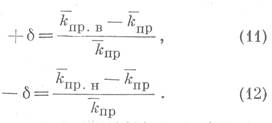
Опираясь на изложенное выше, для заданных значений проницаемости и доверительной вероятности можно рассчитать зависимость предельной относительной ошибки от числа использованных образцов.
Результаты расчета предельной ошибки для средней проницаемости, равной 250 мдарси, и доверительных вероятностей 90 и 98 приведены на рис. 2, где наряду с расчетными кривыми точками нанесены данные, полученные непосредственно при лабораторных исследованиях керна. В качестве исходных данных были использованы значения коэффициентов проницаемости, полученные различными исследователями на образцах из одних и тех же интервалов. Координатами каждой точки являются число образцов, исследованных отдельными авторами, и относительное отклонение средней проницаемости, вычисленной по этим образцам, от средней из общего числа образцов данного пластового пересечения.
Рис. 2 свидетельствует о соответствии теоретических и практических данных. В обоих случаях в области малого числа образцов наблюдается асимметрия, быстро уменьшающаяся при увеличении m; форма кривых согласуется с расположением точек. Это дополнительно подтверждает, что распределение значения коэффициента проницаемости подчинено закону Пуассона.
На рис. 3 изображены кривые δ = f (m), рассчитанные по приведенным выше формулам для доверительной вероятности 90% и различных значений проницаемости. Из рассмотрения кривых следует, что точность определения проницаемости по разрезу зависит от числа исследованных образцов и средней проницаемости оцениваемого интервала.
Кривые рис. 3 дают количественную характеристику отмеченной зависимости и могут быть использованы для оценки предельной и средней ошибок определения средней проницаемости по керну. Например, для 10 образцов определено среднее значение коэффициента проницаемости, равное 350 мдарси. Находим на графике соответствующую точку. Ордината ее равна предельной относительной ошибке (в нашем случае ±26%).
Если предельная относительная ошибка симметрична (или нарушение симметрии очень мало), то она определяет среднюю квадратическую и среднюю ошибки. Для номограммы, изображенной на рис. 3, где α =90%, относительная средняя квадратическая ошибка σ = 0,610 δ и относительная средняя ошибка η = 0,487 δ.
На основании изложенного для девонских терригенных коллекторов Башкирии и Татарии можно сделать следующие выводы.
1. Проницаемость петрографически однородного коллектора значительно изменяется по разрезу в виде случайных отклонений от среднего.
2. Оценка средней проницаемости пласта по керну возможна только вероятностная.
3. Распределение проницаемости по разрезу и по площади подчинено закону Пуассона.
4. Точность определения проницаемости каждого пересечения пласта зависит от количества образцов и величины средней проницаемости.
5. Номограмма, помещенная на рис. 3, рекомендуется для практического применения при оценке точности определения средней проницаемости по керну девонских терригенных отложений Татарии и Башкирии.
ЛИТЕРАТУРА
1. Дахнов В.Н., Долина Л.П. Геофизические методы изучения нефтегазоносных коллекторов. Гостоптехиздат, 1959.
2. Локшин И.А., Султанов С.А. О недостатках изучения коллекторских свойств горных пород по данным лабораторных анализов керна. Татарская нефть, 7, 1957.
3. Саттаров М.М. Оценка точности средней проницаемости пласта методами математической статистики. Сб. трудов; ВНИИ, вып. XXIX, 1960.
4. Xальд А. Математическая статистика с техническими приложениями. ИЛ, 1960.
5. Ван дер Варден. Математическая статистика. ИЛ, 1960.
Волго-Уральский филиал ВНИИгеофизики
Рис. 1. Распределение проницаемости по оси скв. 42 Серафимовского месторождения.
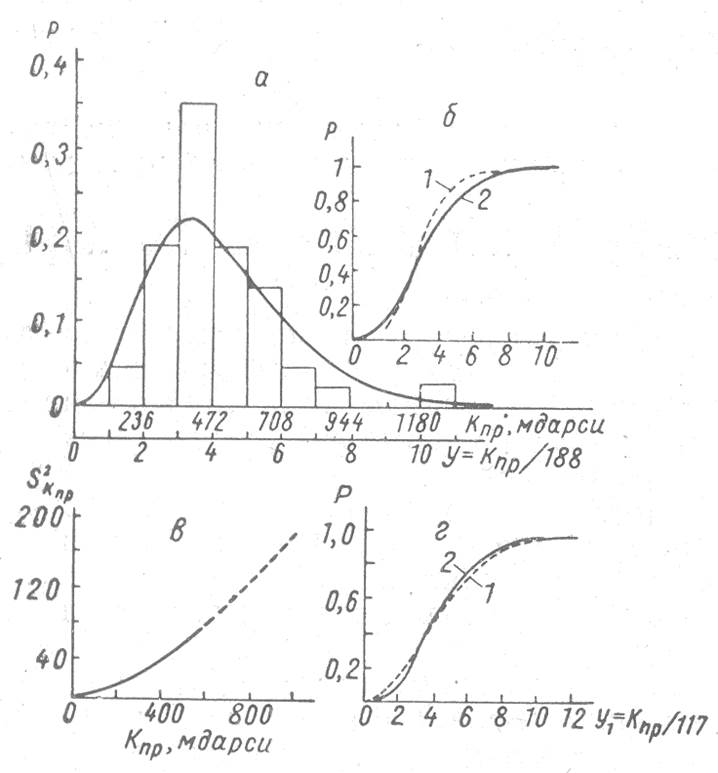
а - плотность распределения: 1 - эмпирическая; 2 - расчетная; б - кривые накопленных частот: 1 - эмпирическая, 2 - расчетная; в - зависимость дисперсии 
от коэффициентов проницаемости Кпр электрически и петрографически однородных интервалов
горизонта ДI Туймазинского, Серафимовского и
Леонидовского месторождений; г - распределение проницаемости нефтеносной части
горизонта ДI Туймазинского месторождения: 1 - эмпирическое, 2 - расчетное.
Рис. 2. Сопоставление расчетных и практических зависимостей относительной ошибки определения средней проницаемости от числа образцов.
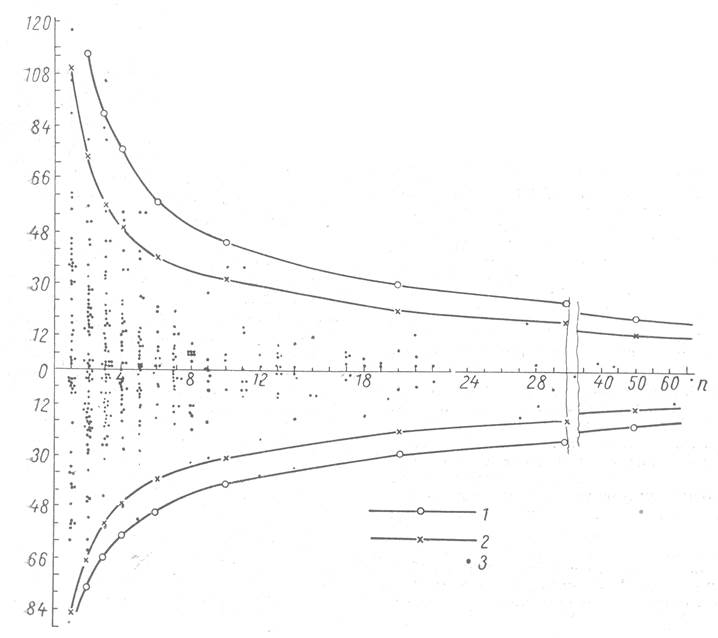
1 -предельная относительная ошибка для α = 90%; 2 - предельная относительная ошибка для α =98%; 3 -относительная ошибка отдельных определений,
Рис. 3. График зависимости предельной относительной ошибки определения средней проницаемости (δКпр) от числа образцов (n).
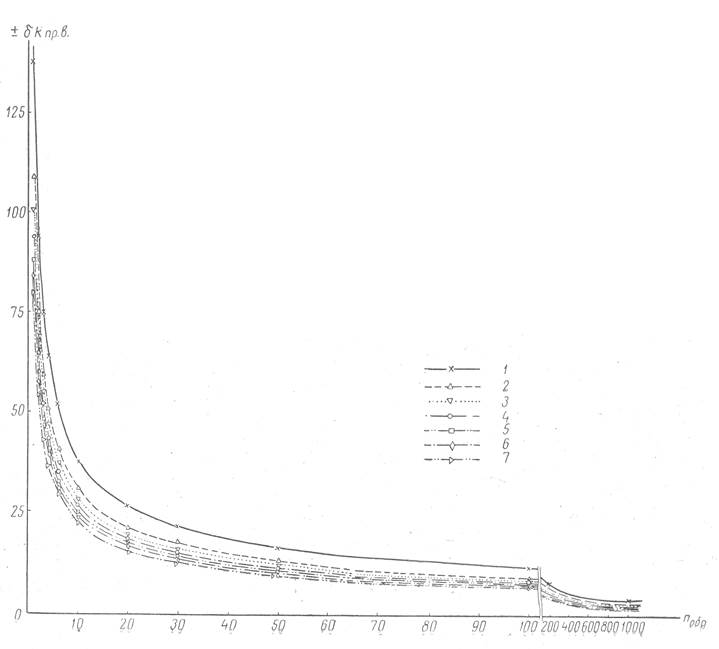
Значения проницаемости (мдарси):1 - 100; 2 - 200; з - 300; 4 - 400;5- 600; в - 800; 7 - 1000.