ВЛИЯНИЕ ДАВЛЕНИЯ НА КОЛЛЕКТОРСКИЕ СВОЙСТВА ПЕСЧАНИКОВ
Настоящая статья - часть работы, выполненная автором в лаборатории горного факультета Калифорнийского университета (г. Беркли, штат Калифорния, США) согласно договору о культурном обмене, заключенному между правительствами СССР и США. Автор искренне благодарен профессору этого факультета И. Фетту за предоставленную возможность использования лабораторного оборудования и за многочисленные практические советы, полученные в процессе работы.
В.М. ДОБРЫНИН
Известно, что коллекторские свойства горных пород, находящихся в глубинных условиях, отличаются от коллекторских свойств тех же пород, измеренных на поверхности при атмосферном давлении. Изменение свойств происходит за счет влияния горного и пластового давлений. Вопрос о количественной стороне этих изменений в связи с развитием глубокого и сверхглубокого бурения приобретает важное значение в нефтяной геологии.
В последнее время в литературе накоплен значительный фактический материал по изучению коллекторских свойств конкретных образцов пород под действием высокого давления. Однако в связи с отсутствием теоретического обобщения этих материалов и вследствие огромного природного разнообразия пород экспериментальные результаты довольно трудно сравнивать или с уверенностью употреблять для количественных прогнозных заключений в новых районах.
В настоящей работе приводится обобщение результатов изменения коллекторских свойств однородных песчаников под давлением, исходя из следующих предпосылок.
Изменение коллекторских свойств (пористости и проницаемости) песчаников под действием давления определяется деформациями, изменяющими объем порового пространства. Величина этих деформаций зависит от степени отсортированности, степени сцементированности породы, наличия и соотношения пластичных и упругих минералов, характера упаковки зерен и, возможно, других факторов, учесть влияние каждого из которых при аналитическом расчете не представляется возможным. Тем не менее, оценить количественно объемные изменения в поровом пространстве можно при помощи коэффициента сжимаемости пор при данном давлении. В этом смысле коэффициент сжимаемости пор представляет собой специфический интегральный параметр, в котором находит отражение влияние всех перечисленных литологических особенностей.
Методика экспериментальных исследований. Для определения коэффициентов сжимаемости пор и изменений пористости под действием внешнего (аналог горного) давления и внутреннего давления жидкости в порах (аналог пластового давления) была использована гидравлическая бомба, устройство которой пояснено на рис. 1.
Перед погружением образцов в бомбу их упаковывали по методике Р. Менна и И. Фетта [1, 2]. Для этого концы образцов закрывались толстостенными латунными чашками с имеющимися в них сквозными отверстиям и соединительными патрубками для линии высокого давления (рис. 2). Затем боковая поверхность образцов закрывалась манжетом из пластмассы.
Перед испытанием манжет погружался на 3-4 ч в органический растворитель, в состав которого входил толуол, при этом диаметр манжета увеличивался примерно на 35%. После покрытия образца и высушивания в течение 12 ч при комнатной температуре диаметр пластмассового манжета становился прежним и манжет очень плотно облегал боковые поверхности образца и латунных чашек. С целью дополнительного уплотнения между латунными чашками и пластмассой помещались кольца из маслостойкой резины.
Для исследований были выбраны два хорошо сцементированных макроскопически однородных кварцевых песчаника: песчаник Торпидо (штат Канзас) с начальной пористостью Кп = 20,2% и проницаемостью Кпр = 45 мд, и песчаник Медина (штат Охайо) с начальной пористостью Кп = 8,7% и проницаемостью Кпр<1 мд. В каждой породе содержалось около 5% глинистого материала, представленного, главным образом, каолинитом и хлоритом.
Из этих пород были приготовлены цилиндрические образцы диаметром 5,1 см и длиной 12,7 см, которые затем под вакуумом насыщались трехнормальным раствором NaCl. Столь высокая концентрация раствора применялась с целью уменьшения разбухания глинистого материала.
Перед измерением каждый образец подвергался двухкратному действию избыточного всестороннего давления, равного 500 ат, для вытеснения пленки раствора из пространства между образцом, латунными чашками и пластмассовым манжетом, а также для уменьшения влияния начальных пластических деформаций породы.
Об изменении объема порового пространства судили по изменению уровня вытесняемой жидкости.
На образцах было проведено две серии опытов при изучении изменений объема пор под давлением. В первой серии внутреннее (пластовое) давление жидкости в порах породы (рпл) было равно атмосферному, а внешнее (горное) давление (рг) изменялось от 0 до 1350 ат. Во второй серии опытов внутреннее давление в порах породы сохранялось равным Рпл = 120 ат, а внешнее давление менялось в пределах Рг = 120-1350 ат. Результаты оказались весьма близкими при сопоставлении их на основе эффективного давления, вычисленного как разность:
Р=Рг-0,85*Рпл.
Поэтому при всех последующих сопоставлениях расчетных кривых с экспериментальными данными использовалась величина эффективного давления.
Коэффициент сжимаемости пор. Абсолютную величину коэффициента сжимаемости пор песчаника (βп) можно определить, наблюдая за изменением объёма пор породы при изменении эффективного давления [3] по формуле:
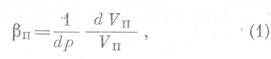
где dVп - изменение объема пор в элементе породы, имеющем объем пор Vп, при изменении эффективного давления на dp.
По экспериментальным данным, приведенным на рис. 3, показано уменьшение коэффициента сжимаемости пор по мере увеличения эффективного давления. Эти данные, дополненные результатами экспериментальных исследований И. Фетта [2], показывают, что в определенном интервале давлений между Pmin и Pmax, зависимости между коэффициентом сжимаемости пор (βп) и логарифмом эффективного давления (lg р) могут быть усреднены и представлены прямыми линиями. Это положение математически можно записать:
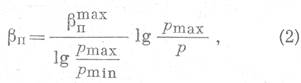
где βпmax - коэффициент максимальной сжимаемости пор, который наблюдается при эффективных давлениях близких к нулю.
Практически βпmax находят путем экстраполяции кривой в точке P = 0.
Для экстраполяции кривой начальный ее участок перестраивался в координатах lg βп - P, поскольку в этой системе координат при давлениях, не превышающих 100 ат, между логарифмом сжимаемости пор и давлением наблюдается зависимость, близкая к прямой линии. Затем величина Pmin находилась, как это показано на рис. 3, в точке пересечения горизонтальной прямой, проходящей через ординату со значением βпmax, и наклонной прямой, усредняющей оставшийся участок зависимости βп=f(р). Такой способ определения основан на том, что в весьма небольшом интервале давлений от 0 до Pmin с точностью, достаточной для практических расчетов, коэффициент сжимаемости пор βп не зависит от приложенного давления и равен своей максимальной величине βпmax. Как показало изучение экспериментальных данных, для различных образцов песчаника Pmin изменяется в пределах от 10 до 20 ат.
Значения Pmax находят путем экстраполяции прямолинейных зависимостей, изображенных на рис. 3, до пересечения их с осью абсцисс. Математически Pmax - давление, при котором коэффициент сжимаемости пор равен нулю. Однако это только прием, позволяющий упростить задачу в области очень высоких давлений, где изменения коэффициента сжимаемости пор столь малы, что для практических расчетов ими можно пренебречь. Фактически Pmax - давление, выше которого не наблюдается заметных изменений в коэффициенте сжимаемости пор, а сам коэффициент приобретает очень небольшое значение, близкое к значению коэффициента сжимаемости зерен скелета породы. Обобщение всех имеющихся экспериментальных данных показывает, что для различных песчаников найденное таким путем значение Pmax находится в пределах от 1500 до 2000 ат. Совершенно очевидно, что для некоторых типов песчаника величина Ртах окажется выше критического давления, при котором уже наблюдаются заметные разрушения скелета породы. Однако и в этом случае введение Pmax оправдывает себя, так как позволяет математически описать изменения упругих свойств указанных песчаников в интервале давлений, не превышающих давлений разрушения скелета пород.
Изменение пористости песчаников с давлением. Относительное уменьшение коэффициента пористости ΔКп/Кп породы при увеличении всестороннего давления можно выразить через относительное уменьшение объема норового пространства элемента горной породы ΔVп/Vп и относительное уменьшение внешнего объема этого элемента ΔV/V по формуле:
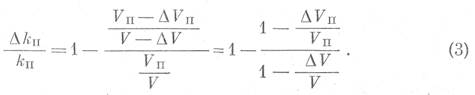
Пренебрегая влиянием сжимаемости зерен горной породы, можем написать следующее уравнение:
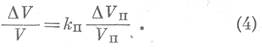
Подставив значение уравнения (4) в уравнение (3), получим:
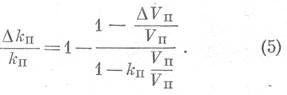
Как уже упоминалось выше, можно принять, что в узком интервале давления 0<P<Pmin коэффициент сжимаемости пор практически мало зависит от давления и может быть принят равным максимальной величине, т. е. βп=βпmax. Тогда относительное уменьшение объема пор, которое будет наблюдаться при действии эффективного давления, можно определить с учетом уравнений (1) и (2) следующим образом:
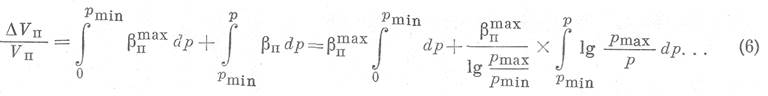
После интегрирования этого выражения получим:
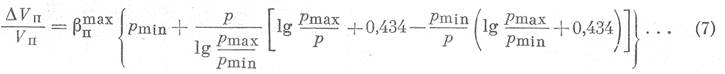
Обозначим в последнем уравнении:
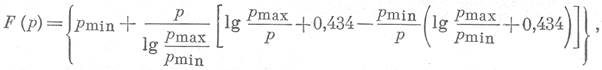
после чего уравнение (7) перепишется:
![]()
Таким образом, при помощи уравнения (8) удалось представить величину относительного уменьшения объема пор в виде двух множителей. Первый множитель, βпmax зависит только от свойств породы, в то время как второй - F(p) - от величины эффективного давления.
Подставляя найденное при помощи уравнения (8) значение ΔVп/Vп в уравнение (5), будем окончательно иметь:
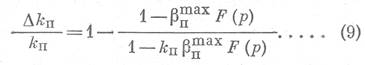
На рис. 4 изображены кривые относительного изменения коэффициента пористости с давлением, рассчитанные по уравнению (9). При расчете были заданы следующие средние значения постоянных давления: Pmin=13,5 ат и Рmax=1700 ат. Расчет произведен до давления (р = 1400 ат), при котором в настоящее время получены экспериментальные данные.
На рис. 4 приведены экспериментальные данные, хорошо соответствующие расчетным кривым.
Таким образом, коэффициент максимальной сжимаемости пор является тем основным фактором, который определяет величину изменения пористости различных типов песчаников при любом давлении, т.е. на заданной глубине. Экспериментальное изучение этого коэффициента показывает, что для большинства исследованных до настоящего времени сцементированных песчаников его значения могут находиться в пределах от βпmax = 0,75х10-4 ат-1 до βпmax= 3,0х10-4 ат-1. Это означает (рис. 3), что при изменении эффективных давлений от 0 до 1400 ат (глубина около 9000 м) возможное изменение коэффициента пористости сцементированных песчаников находится в пределах от 0 до 10%. Имеют место случаи, когда вследствие своеобразной упаковки зерен и распределения в породе упругих и пластичных минералов величина βпmax может достичь значений 7,0х10-4 ат-1 и более, что будет соответствовать и большим пределам изменения пористости этих пород под давлением.
Изменение проницаемости песчаников с давлением. Известные в настоящее время экспериментальные исследования [4, 5] свидетельствуют о значительном изменении коэффициента проницаемости пород под действием давления. Основную роль при этом играет сужение поровых каналов при воздействии давления, а также в какой-то мере усложнение их конфигурации. На наш взгляд, первая причина является главной. Следовательно, и в этом случае при помощи коэффициента сжимаемости пор породы можно количественно судить об изменении ее проницаемости при действии всестороннего давления.
Для доказательства этого положения возьмем уравнение Маршалла [6], выведенное для идеализированной модели породы, поры которой представлены набором параллельных цилиндрических каналов самых различных диаметров с резкими переходами от одного диаметра к другому в пределах каждого канала.
По Маршаллу, коэффициент проницаемости (Кпр) такой модели будет вычислен:
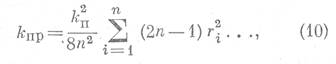
где ri - радиус i-того канала, n - число каналов, Кп - коэффициент пористости модели.
Под действием бесконечно малого приращения эффективного давления (dp) коэффициент проницаемости уменьшится на величину dКпр, а коэффициент пористости на величину dКп, что можно выразить математически, переписав уравнение (10) в следующем виде:
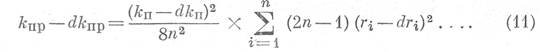
Разделив уравнение (11) на уравнение (10), получим:
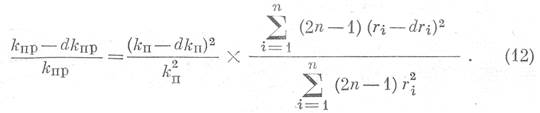
Если учесть, что в условиях поставленной задачи, при малых значениях dp, величина относительного изменения радиуса поровых каналов dri/ri представляет собой также малую величину, то уравнение (12) можно преобразовать:
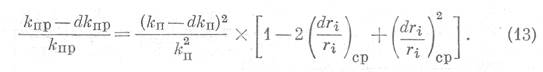
Пренебрегая бесконечно малыми величинами второго порядка
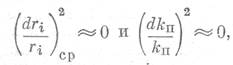
получим
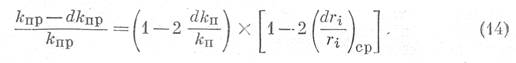
Среднее
значение изменения радиуса поровых каналов 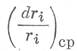 должно быть
пропорционально изменению объема порового пространства, что можно также
записать:
должно быть
пропорционально изменению объема порового пространства, что можно также
записать:
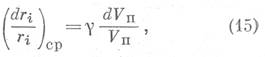
где γ - коэффициент пропорциональности.
С учетом уравнения (1), уравнение (15) можно переписать в виде:
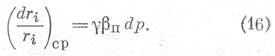
Если пренебречь малым изменением внешнего объема dV/V элемента породы под действием приращения давления dp, то согласно уравнению (3) будем иметь:
![]()
Подставляя
значения 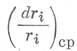 и dКп/Кп из
уравнений (16) и (17) в уравнение (14), и, преобразуя это уравнение, получим:
и dКп/Кп из
уравнений (16) и (17) в уравнение (14), и, преобразуя это уравнение, получим:
![]()
Вторым членом этого уравнения можно также пренебречь как бесконечно малой величиной второго порядка. Тогда для вычисления относительного изменения проницаемости под действием эффективного давления Р, необходимо проинтегрировать уравнение (18):
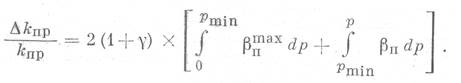
После интегрирования (см. уравнение 6, 7 и 8) будем иметь (В первом приближении было принято, что коэффициент пропорциональности γ не зависит от давления на всем интервале интегрирования.):
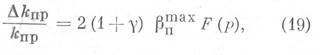
или несколько в другом виде:
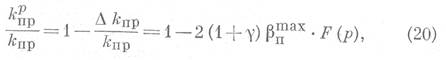
где КпрР- значение коэффициента проницаемости при давлении р.
В общем случае следует предположить, что коэффициент пропорциональности γ, введенный в уравнение (15), зависит от сжимаемости пор породы и от степени однородности пор по их размерам, поскольку большей сжимаемостью обладают поры большого размера и влияют эти поры в значительной степени на проницаемость и ее изменение. На рис. 5 изображена зависимость коэффициента у от коэффициента максимальной сжимаемости пор, полученная при изучении песчаников с неравномерными по размеру порами. Для построения этой зависимости было использовано уравнение (20) и экспериментальные данные - значения КпрР/Кпр и βпmax*F (р). Эти данные, на основании которых определен коэффициент γ, получены на песчанике Торпидо, а также заимствованы из опубликованной работы И. Фетта [5]. Типичный пример песчаника с неравномерными по размерам порами представляет песчаник Торпидо, гистограмма распределения пор которого показана на рис. 6.
По формуле (20) с учетом эмпирической зависимости, изображенной на рис. 5, были рассчитаны кривые изменения коэффициента проницаемости песчаников (КпрР/Кпр*100, %) в зависимости от эффективного давления р. Эти кривые для сцементированных песчаников с неравномерными по размерам порами изображены на рис. 7. Рассчитанные кривые удовлетворительно согласуются с экспериментальными данными, полученными при изучении газопроницаемости сухих песчаников, К сожалению, имеющиеся в настоящее время экспериментальные материалы, не позволяют полнее изучить значение коэффициента у для пород с более однородными порами.
В отличие от пористости проницаемость песчаников изменяется с давлением в значительно более широком диапазоне. Например, для пород с высокими значениями коэффициента максимальной сжимаемости пор (βпmax= 3,0х10-4 ат-1 и выше) при эффективных давлениях, достигающих 1400 ат, коэффициент проницаемости может уменьшиться более чем вдвое по сравнению со значением, измеренным при атмосферных условиях.
В заключение необходимо отметить, что изменение коллекторских свойств песчаников (пористости и проницаемости) под действием всестороннего давления можно объяснить, введя понятие о коэффициенте максимальной сжимаемости пор. Зная пор и величину эффективного давления, можно делать количественные заключения об изменении коллекторских свойств песчаников с глубиной. Кроме того, специальные исследования [7] показывают, что при помощи коэффициента максимальной сжимаемости пор удается установить изменение с давлением таких важнейших физических параметров песчаников, как плотность, удельное электрическое сопротивление и скорость упругих волн. Поэтому при лабораторном изучении физических свойств коллекторов, залегающих на значительных глубинах, изучению коэффициентов максимальной сжимаемости породы должно быть уделено такое же внимание, как и изучению основных стандартных физических параметров. Значение коэффициента максимальной сжимаемости пор экспериментально может быть определено при сравнительно низких давлениях, используя для этого простую и дешевую аппаратуру. Помимо прямых лабораторных определений, принципиально возможны косвенные методы определения коэффициентов максимальной сжимаемости пор, например, по данным акустического метода исследования скважин [7]. Скорость распространения упругих волн в породах, определяемая по этому методу, существенно зависит от коэффициента, максимальной сжимаемости пор [7]. Это позволяет, зная величину скорости упругих волн и некоторые другие параметры породы, определить коэффициент максимальной сжимаемости пор. По мере накопления фактического материала, по-видимому, возможно построение корреляционных связей между коэффициентами максимальной сжимаемости пор и литологическими характеристиками пород определенного типа.
ЛИТЕРАТУРА
1. Mann R. L. Effect of Роге Fluids on the Elastic Properties of Sanstone. M. S. Thesis. University of California, Berkeley, 1959.
2. Fatt I. Compressibility of Sand stones at Low to Moderate Pressure. Bull. A. A. P. Y., vol. 42, № 8, 1958.
3. Щeлкачeв В.H. Разработка нефтеводоносных пластов при упругом режиме. Гостоптехиздат, 1959.
4. Marshall A. Relation Between Permeability and Size Distribution of Pores. J. Soil Si. vol. 9, N 1, 1958.
5. Fatt I. The Effect of Overburden Pressure on Relative Permeability. J. Petr. Tech., October, 1953.
6. Кусаков М.М., Гудок Н. С. Нефт. хоз., № 6, 1958.
7. Добрынин В.М. Труды МИНХ и ГП, вып. 41, Гостоптехиздат, 1962.
Рис. 1. Схема гидравлической бомбы для изучения свойств горных пород под давлением.
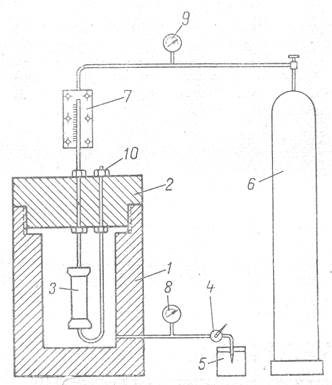
1 - корпус бомбы; 2 - крышка бомбы; 3 - образец; 4-масляная помпа; 5-масляный резервуар; 6 - баллон со сжатым газом; 7 - градуированная пипетка для определения количества вытесненной из образца жидкости при наличии пластового давления; 8 - манометр для измерения давления в бомбе; 9 - манометр для измерения внутреннего давления в порах породы; 10 - заглушка.
Рис. 2. Схема упаковки образца перед изучением под высокими давлениями.
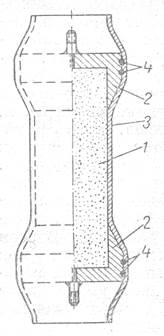
1 - образец; 2 -латунная чашка; 3 - пластмассовый манжет; 4 - уплотнительные кольца из маслостойкой резины.
Рис. 3. Кривые изменения коэффициента сжимаемости пор (βп) от эффективного давления (р).
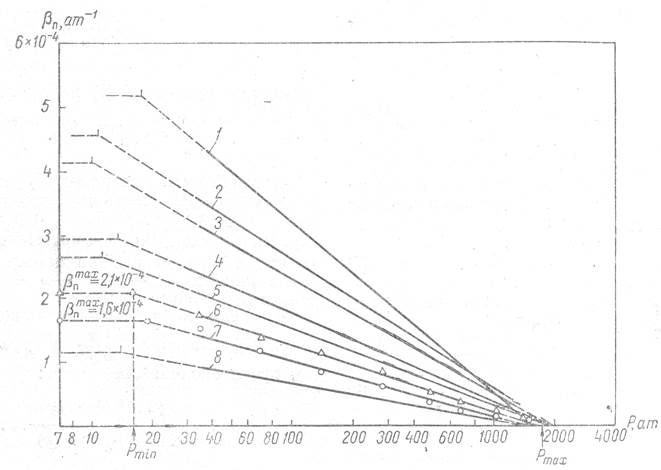
1 - 5 и 8 - песчаники, исследованные И. Феттом в работе [2]; 6 - песчаник Медина(Δ); 7 - песчаник Торпидо (О).
Рис. 4. Сопоставление
расчетных кривых относительного изменения коэффициента пористости ΔКп/Кп
от эффективного давления с экспериментальными данными. 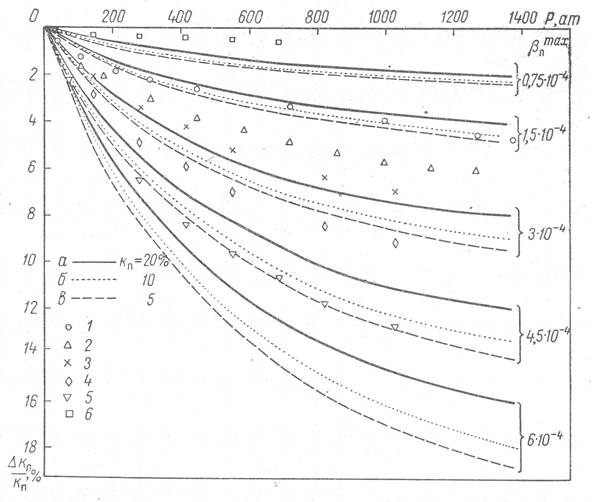
Модули: коэффициент максимальной сжимаемости пор (βпmax) и коэффициент пористости (Кп). Экспериментальные данные: 1 - песчаник Торпидо (βпmax= 1,6х10-4 ат-1 Кп=20,2%); 2-песчаник Медина (βпmax=2,1х10-4 ат-1, Кп=8,7%); 3 - песчаник Хантингтон Бич [2] (βпmax=2,9х10-4 ат-1, Кп=24%; 4 -песчаник Сан Джоакин Валлей[2] (βпmax=3,2х10-4 ат-1, Кп=8,9 %); 5 - песчаник Сан Джоакин Валлей (βпmax=5,1х10-4 ат-1, Кп=19,9 %); 6-искусственный керн из сцементированных зерен окиси алюминия [2] (βпmax=0,37х10-4 ат-1; Кп=28,6%).
Рис. 5. Эмпирическая зависимость коэффициента γ от коэффициента максимальной сжимаемости пор (βпmax) для песчаников с неравномерными по размеру порами.
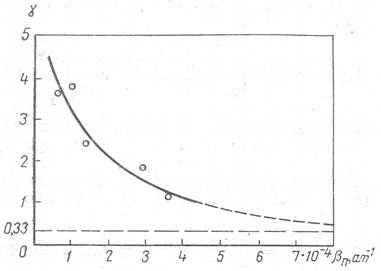
Рис. 6. Гистограмма распределения пор различных размеров в песчанике Торпидо.
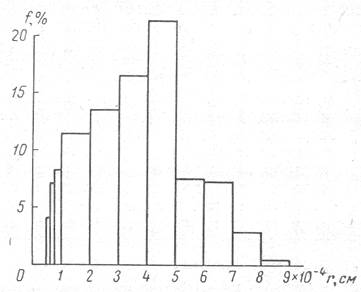
Рис. 7. Сопоставление расчетных кривых относительных изменений коэффициента проницаемости песчаников (КпрР/Кпр•100, %) от эффективного давления (р) с экспериментальными данными.
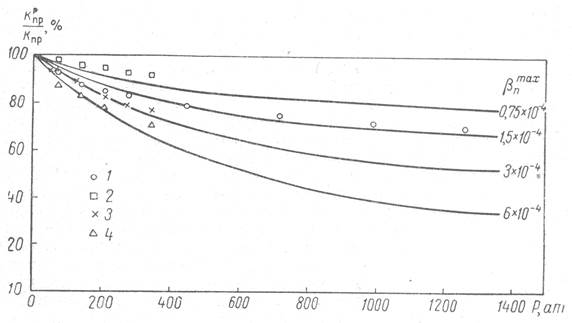
Модуль кривых: коэф. макс, сжимаемости пор (βпmax). 1 -песчаник Торпидо; 2-песчаник Базал Тускалуса [5]; 3 - песчаник Южная Калифорния[5]; 4 - песчаник бассейна Лос-Анжелос [5].