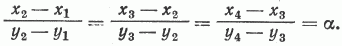
|
УДК 553.98:550.832 |
Корреляция геофизических разрезов скважин на ЭВМ
Ш.А. ГУБЕРМАН, Е.Е. КАЛИНИНА, М.И. ОВЧИННИКОВА, В.Ф. ОСИПОВ (МИНХиГП)
Корреляция разрезов скважин - одна из труднейших задач геологии и геофизики, которую приходится решать с привлечением самой разнообразной информации. В данной статье предпринята попытка промоделировать процессы расчленения и корреляции геофизических разрезов скважин на ЭВМ. Корреляция пластов в осадочных толщах может преследовать две цели: 1) установление в разрезах различных скважин точек, которые в процессе накопления осадков одновременно принадлежали поверхности осадконакопления (синхронных точек); 2) выявление в разрезах скважин интервалов, принадлежащих сейчас или некогда одному геологическому телу (Ю.А. Воронин, 1968).
Расчленение геофизических разрезов скважин с помощью ЭВМ. Представляется, что разрез состоит из подразделений нескольких уровней - крупных, однородных в определенном смысле интервалов, каждый из которых имеет более мелкие интервалы, а те, в свою очередь, еще более мелкие. При этом мощности интервалов в разрезе содержат группы характерных для каждого уровня, предпочтительных значений. Нужно описать разрез в несколько этапов, сначала грубо, без подробностей, затем детализировать его, расчленяя каждый из выделенных на предыдущем уровне интервалов по такому же принципу. В практике этому соответствует разбивка разреза на толщи, пачки, пласты, пропластки.
Алгоритм в первую очередь отделяет на геофизической кривой интервалы с повышенными значениями амплитуд от интервалов с пониженными. Положительные и отрицательные аномалии амплитуды рассматриваются относительно ее скользящего среднего значения, определяемого в каждой точке кривой как средняя величина отсчетов амплитуд в соседних точках на заданном интервале глубин. Интервал осреднения выбирается достаточно большим, например в одну треть длины очередного интервала расчленения. После того, как на исследуемом участке геофизической кривой f(x) проведена скользящая средняя линия f (х), строится функция расстояний каждой точки кривой от соответствующего ей значения скользящего среднего. В результате ось х разбивается на N интервалов с постоянными знаками этой функции (a1+ , a2-, a3+ ,..., am-). Пусть минимальная длина интервала из этой разбивки lj и lj<=L, где L зафиксировано. Исключим интервал aj. Для этого у aj меняется знак и он объединяется с соседними aj-1 и aj+1 в один интервал разбивки. Выбор минимального интервала и процедура его исключения из разбивки с объединением интервалов повторяется до тех пор, пока длины всех оставшихся интервалов не окажутся больше L. Полученное расчленение охарактеризуем числом N(L) оставшихся интервалов и вновь повторим процедуру объединения с большим L. Так, изменяя L, получаем функцию N(L). Эта функция монотонна (с увеличением L число интервалов не возрастает). Она характеризует степень организованности кривой.
Рассмотрим наиболее характерные случаи ( рис. 1 ).
На рисунке показано, что интервалы разбиения кривой имеют не любую длину, а распадаются на группы: длиной не менее LI, что соответствует наиболее грубому описанию кривой f(x), не менее LII, не менее LIII (что соответствует наиболее подробному описанию кривой). Чем ближе полученная реальная функция N(L) к кривой (см. рис. 1 , Б), тем организованнее исходная кривая f(x), тем больше возможностей для краткого ее описания. В идеальном случае f(x) должна представлять собой ступенчатую линию, которая может иметь всего два значения, например, +1 и -1. Для такой кривой разделение на пачки, пласты и пропластки должно проводиться в один прием, для реальных же диаграмм - рекуррентно. Каждый из интервалов, выделенных на первом этапе расчленения, выступает в дальнейшем как самостоятельный объект исследования и подвергается более детальному расчленению. При этом на каждом этапе расчленения вырабатываются свои критерии выбора интервала осреднения для построения f(х) и пороговой мощности (Lпор).
Может оказаться, что ни для одной из возможных f(х) не будет найдена такая функция N (L), обладающая “ступенькой”, т.е. не будет определена Lпор интервалов разбивок. Это означает, что исследуемый разрез не соответствует принятой модели, или, другими словами, не может быть кратко (и обстоятельно) описан. После того, как на одной из геофизических кривых по описанному алгоритму выделены пачки, пласты и пропластки, с помощью любого из уже разработанных алгоритмов отбивки границ пластов уточняются границы выделенных пластов (сначала по каждому методу отдельно, а затем, по комплексу методов).
Сопоставление геофизических разрезов скважин. В основу предлагаемых алгоритмов сопоставления геофизических разрезов скважин положена геометрическая модель геологических разрезов, основанная на следующих предположениях [4]: 1) геологический разрез состоит из нескольких этажей, каждый из которых построен по своему геометрическому закону; 2) внутри каждого этажа мощности входящих в него пластов изменяются от разреза к разрезу пропорционально расстоянию между разрезами, т. е. они подчиняются своему (для каждого этажа) закону перспективного соответствия. Пласты в разрезах залегают либо горизонтально, либо веерообразно. Это, вероятно, справедливо только для морских отложений, где поверхность осадконакопления в основном формировалась под действием гравитационных сил. Предполагается, что в дальнейшем пласты могли быть несколько смяты, однако границы их остаются параллельными и порядок не изменяется.
Представим, что исследуются отложения, в которых границы между пластами расположены веерообразно. Две скважины, пробуренные в этих отложениях, встретят границы пластов в точках на глубине x1, х2, х3, ... для одной и у1, y2, y3, ... для другой. В данных отложениях плоскости границ пересекаются по одной прямой и для разрезов этих скважин удовлетворяют условиям перспективного соответствия, т. е.
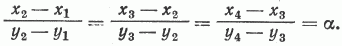
Возможно, что расположение пластов в этих скважинах остается неизменным. Этот принцип впервые был использован в схеме Б. Жеховского [3]. Берется плоскость с прямоугольной системой координат. По одной оси откладываются глубины границ пластов первой скважины, по другой - второй. Точки с координатами (x1, y1) (х2, y2), ... наносятся на координатную плоскость. В результате они укладываются на монотонно падающую линию, отражающую принцип последовательности в напластовании осадков. Но так как границы пластов подчиняются принципу перспективного соответствия, то эта плавная линия есть прямая, угол наклона которой b к оси х соответствует постоянному коэффициенту a соотношения мощностей пластов для заданных интервалов разрезов двух скважин (b = arctg a). Если мощности пластов равны и пласты параллельны, то b = 45°. Таким образом, полученная корреляционная прямая отражает закон корреляции разрезов в сопоставляемых скважинах [2]. Чаще всего разрез оказывается состоящим из нескольких этажей, каждый из которых характеризуется своей корреляционной прямой со своим углом наклона b.
Таким образом, линия корреляции на графике в общем состоит из нескольких прямолинейных отрезков. Анализ корреляционных графиков позволяет: 1) выделить прямолинейные участки корреляции разрезов, каждый из которых соответствует геологической эпохе, когда отлагавшиеся осадки были неподвижны друг относительно друга или перемещались с одной и той же скоростью; 2) обнаружить места несогласий в разрезе по излому или разрыву корреляционной линии. По взаимному расположению корреляционных прямых на графике можно судить о типах несогласий в разрезах: взброс характеризуется параллельным переносом нижележащей прямой вверх, сброс - переносом прямой вниз, перерыв в осадконакоплениях - изменением наклона корреляционной прямой ( рис. 2 , А, Б, В); 3) в ряде случаев оказывается возможным уточнить корреляцию разрезов, если одна или несколько точек на графике не попадают на уверенно проведенную прямую, например, при литолого-фациальных замещениях (см. рис. 2 , Г). Таким образом, задача сопоставления разрезов заключается в том, чтобы, во-первых, найти для каждого этажа свой коэффициент соотношения мощностей, а во-вторых, определить границы этажей. Для этого разработаны два следующих алгоритма корреляции.
Алгоритм сопоставления границ пластов, выделенных на геофизических диаграммах, основан на поиске функции минимальных рассогласований между соответствующими границами двух коррелируемых разрезов. Эта функция определяется следующим образом: f = (xi) = xi - yi0, где i - номера границ первой скважины; j0 - дает минимум по j выражения (хi-yj+D0); j - номера границ второй скважины, D0=x1-y1. Рассмотрим снова известные случаи залегания пластов. При горизонтальном залегании в разрезах двух скважин функция рассогласования между сопоставляемыми границами f(xi-yj) равна нулю на всем протяжении разрезов ( рис. 3 , А). В случае, когда пласты смяты, но параллельны, она равна постоянной разности между соответствующими границами (см. рис. 3 , Б). При веерообразном залегании пластов в разрезах расстояние между коррелируемыми границами возрастает линейно. Здесь функции минимальных рассогласований между соответствующими границами ложатся на прямую линию с углом наклона b = arctg(a-1), где a - коэффициент отношения мощностей (см. рис. 3 , В). Пусть требуется сопоставить два разреза. Алгоритм работает следующим образом. Строится функция минимальных рассогласований между границами f (xi-уj). Выделяются участки, соответствующие ее линейному ходу, которые запоминаются как вероятные участки корреляции. Затем разрезы сдвигаются относительно друг друга на один пласт и повторяется процедура построения и оценки данной функции до тех пор, пока не будут просмотрены все варианты сопоставления границ. Из полученных таким образом вариантов корреляции выбираются те, которые удовлетворяют принципу упорядоченности, т.е. соответствующие участки вероятной корреляции - участки линейности f (хi-yi) - располагаются в каждой из скважин в одинаковом порядке. Из оставшихся выбираются варианты, удовлетворяющие наилучшим образом принципу перспективного соответствия, т.е. участки линейности, обладающие наименьшей дисперсией точек. Реально нет необходимости в переборе всех вариантов. Обычно имеется предварительная информация, которая позволяет ограничить возможные интервалы корреляции.
Алгоритм корреляции нерасчлененных геофизических диаграмм основан также на принципе похожести коррелирующих участков диаграмм в предположении, что относительные свойства пластов мало изменяются на рассматриваемой территории от разреза к разрезу. Мерой похожести выбрана величина нормированного коэффициента корреляции между сравниваемыми участками диаграмм (k). Чем более сходны участки, тем k ближе к +1. Алгоритм работает следующим образом. Одна из диаграмм произвольно разбивается на ряд участков. Вычисляется функция корреляции между каждым из этих участков и всеми участками такой же длины второй диаграммы. Эта функция имеет максимумы в некоторых точках. На корреляционном графике на одной оси отмечаются глубины первой диаграммы, на другой - второй. Для каждого из участков корреляции на координатную плоскость наносится ряд точек, первая координата которых соответствует глубине начала участка по первой диаграмме, а вторая - той глубине начала участка по второй, где функция корреляции достигла максимума Км, а также отмечается величина этого максимума. В самых благоприятных для корреляции случаях точки на графике, соответствующие наибольшему в каждом ряду максимуму Кмм, ложатся на корреляционную прямую, идущую под углом 45°, если мощности сопоставляемых интервалов равны, или под некоторым углом b, характеризующим закон соотношения мощностей на этих интервалах разрезов двух скважин. Может оказаться, что на каком-то отрезке функция корреляции достигнет значения Кмм не против соответствующего участка на второй диаграмме, а в другом месте. В такой ситуации исходя из принятой модели разрезов можно провести корреляцию не только по точкам с Кмм, но и через точки Км или даже там, где вообще отсутствует Км, если корреляция выше- и нижележащих отложений хорошо описывается выбранной корреляционной прямой.
Далее, через каждые три точки на корреляционном графике, соответствующие Кмм, проводится прямая, на которой отмечаются все другие Км, которые попадают с некоторым заданным допуском на эту прямую. Каждая такая прямая представляет собой вероятный вариант корреляции разрезов. Затем все полученные варианты анализируют, сравнивают и находят наиболее вероятные из них в смысле наилучшего удовлетворения принципам упорядоченности, перспективного соответствия, а также принципу похожести - по наибольшему среднему значению коэффициента корреляции точек, расположенных на корреляционной прямой. Второй из алгоритмов корреляции позволяет проводить ее без предварительного расчленения диаграмм или без надежных результатов расчленения.
Пример корреляции геофизических разрезов скважин с помощью ЭВМ. По описанным выше алгоритмам авторами были составлены программы, с помощью которых методика автоматической корреляции опробована на различных месторождениях. Приведем результаты корреляции карбонатных отложений верхнего девона - нижнего карбона платформенной части Пермской области на примере скв. 139, 147, 149 Савинской площади. Каждая из скважин представлена диаграммой градиент-зонда N2,0A0,5B, описывающей около 800 м разреза. Исходные диаграммы оцифрованы с шагом 1 м и попарно непрерывно скоррелированы. Рассмотрим более подробно корреляционный график пары скв. 147 и 139, полученный при машинной корреляции с помощью графопостроителя (рис. 4, А). На графике по осям нанесены глубины и сами кривые КС разрезов этих скважин, на корреляционное поле - точки пересечения границ реперов (I-VIII), выделенных геологами “вручную”. Кроме того, на графике обозначены полученные при работе программы точки корреляции соответственно их рангам для каждого из участков корреляции, а также корреляционные прямые, построенные с помощью программы по наиболее “сильным” из точек. Видно, что исследуемый разрез делится на четыре интервала. Первым 250 м разреза соответствует отрезок прямой; проходящей под углом 43° к оси глубин скв. 147, что свидетельствует о небольшом пропорциональном сокращении мощности разреза скв. 139. Этот отрезок характеризуется довольно высоким средним значением максимумов (К1 = 0,64). Второй отрезок, представляющий следующие 250 м разреза, имеет угол наклона 45°, что свидетельствует о равномерном залегании пластов в этом интервале. Корреляция здесь менее надежна, так как соответствующее значение К2=0,57. Нижний, четвертый интервал разреза мощностью около 200 м также выражен прямой, проходящей под углом 45° к осям графика, с очень сильным 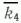 = 0,94, что говорит о большой надежности корреляции на этом интервале разреза. Третий интервал (150 м) характеризуется двумя слабыми близкими прямыми с
= 0,94, что говорит о большой надежности корреляции на этом интервале разреза. Третий интервал (150 м) характеризуется двумя слабыми близкими прямыми с 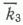 = 0,44 и
= 0,44 и 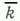 =0,43. Здесь требуется уточнение результатов с помощью дополнительных геофизических методов. Интересно отметить, что именно в этой части разреза геологи предполагают наличие рифогенных образований, которые и могли нарушить регулярность залегания пластов. Разрывы линии корреляции на графике говорят о последовательном выпадении из разреза скв. 147 интервалов 5; 20; 30 м. Видно, что на линию корреляции хорошо ложатся точки корреляции большинства реперов. Аналогично построены корреляционные графики скв. 147, 149 и 139, 149 (см. рис. 4 , Б, В). В обоих случаях был получен целый “веер” почти равноценных прямых на первом и втором интервалах разреза, по одной надежной - на четвертом и слабые прямые на третьем. Из “веера” прямых, характеризующих вероятные варианты корреляции на первых двух интервалах каждого из графиков, было выбрано по одной наиболее достоверной в смысле наибольшего удовлетворения единому принципу перспективного соответствия путем тройного сопоставления графиков парной корреляции [1]. Отрезки линии корреляции четвертого интервала разреза также оказались согласованными на всех трех графиках. На третьем же интервале таких согласованных отрезков не оказалось, что может служить подтверждением гипотезы о рифогенных образованиях на данном интервале разреза. Затем каждая из диаграмм была автоматически расчленена и границы выделенных пластов продолжены на графиках до пересечения с корреляционными прямыми. Большинство точек пересечения соответствующих границ легло на линию корреляции, в некоторых же местах наблюдается отход точек от прямых, что может свидетельствовать о наличии литолого-фациальных замещений в соответствующих местах разреза. Таким образом, можно проводить детальную корреляцию любых интересующих геолога интервалов разреза. Независимо была проведена парная корреляция разрезов тех же скважин с помощью программы сопоставления границ пластов, выделенных на ЭВМ. Результаты такой попластовой корреляции оказались близкими к результатам непрерывной корреляции, что позволяет судить о достаточной надежности результатов машинной корреляции исследуемых разрезов.
=0,43. Здесь требуется уточнение результатов с помощью дополнительных геофизических методов. Интересно отметить, что именно в этой части разреза геологи предполагают наличие рифогенных образований, которые и могли нарушить регулярность залегания пластов. Разрывы линии корреляции на графике говорят о последовательном выпадении из разреза скв. 147 интервалов 5; 20; 30 м. Видно, что на линию корреляции хорошо ложатся точки корреляции большинства реперов. Аналогично построены корреляционные графики скв. 147, 149 и 139, 149 (см. рис. 4 , Б, В). В обоих случаях был получен целый “веер” почти равноценных прямых на первом и втором интервалах разреза, по одной надежной - на четвертом и слабые прямые на третьем. Из “веера” прямых, характеризующих вероятные варианты корреляции на первых двух интервалах каждого из графиков, было выбрано по одной наиболее достоверной в смысле наибольшего удовлетворения единому принципу перспективного соответствия путем тройного сопоставления графиков парной корреляции [1]. Отрезки линии корреляции четвертого интервала разреза также оказались согласованными на всех трех графиках. На третьем же интервале таких согласованных отрезков не оказалось, что может служить подтверждением гипотезы о рифогенных образованиях на данном интервале разреза. Затем каждая из диаграмм была автоматически расчленена и границы выделенных пластов продолжены на графиках до пересечения с корреляционными прямыми. Большинство точек пересечения соответствующих границ легло на линию корреляции, в некоторых же местах наблюдается отход точек от прямых, что может свидетельствовать о наличии литолого-фациальных замещений в соответствующих местах разреза. Таким образом, можно проводить детальную корреляцию любых интересующих геолога интервалов разреза. Независимо была проведена парная корреляция разрезов тех же скважин с помощью программы сопоставления границ пластов, выделенных на ЭВМ. Результаты такой попластовой корреляции оказались близкими к результатам непрерывной корреляции, что позволяет судить о достаточной надежности результатов машинной корреляции исследуемых разрезов.
Итак, описанные алгоритмы позволяют автоматизировать расчленение и корреляцию разрезов в достаточно простых случаях, а в более сложных - помогают выбрать наиболее обоснованный вариант корреляции. Возможны случаи, когда алгоритмы не дадут удовлетворительных результатов. Это будет означать, что строение исследуемых разрезов не соответствует модели, заложенной в основу алгоритмов. Рассмотренные алгоритмы позволяют оценить надежность полученных результатов по степени отклонения от принципов похожести, упорядоченности и перспективного соответствия.
СПИСОК ЛИТЕРАТУРЫ
Поступила 13/II 1980 г.
Рис. 1. Два крайних случая, характеризующих степень организованности кривой с интервалами разбивок всевозможной длины (A) и имеющими ряд предпочтительных разбивок (Б)
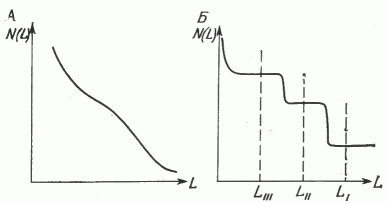
Рис. 2. Типы нарушений в разрезах и соответствующие им корреляционные графики.
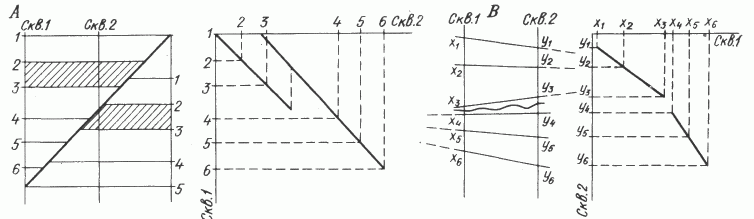
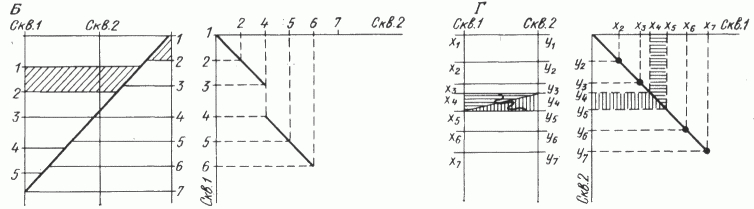
А - взброс; Б - сброс; В - перерыв в осадконакоплениях; Г - литолого-фациальное замещение
Рис. 3. Модельный пример сопоставления расчлененных разрезов.
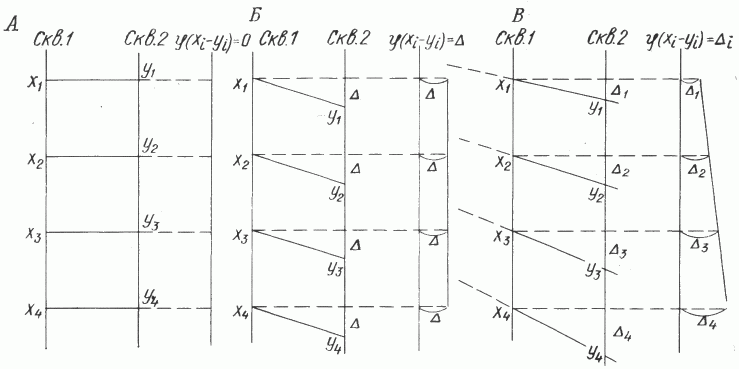
Залегание пластов: А - горизонтальное; Б - параллельное (пласты смяты); В - веерообразное
Рис. 4. Корреляционные графики разрезов скв. 147 и 139 (А), 147 и 149 (Б), 139 и 149 (В) Савинской площади.
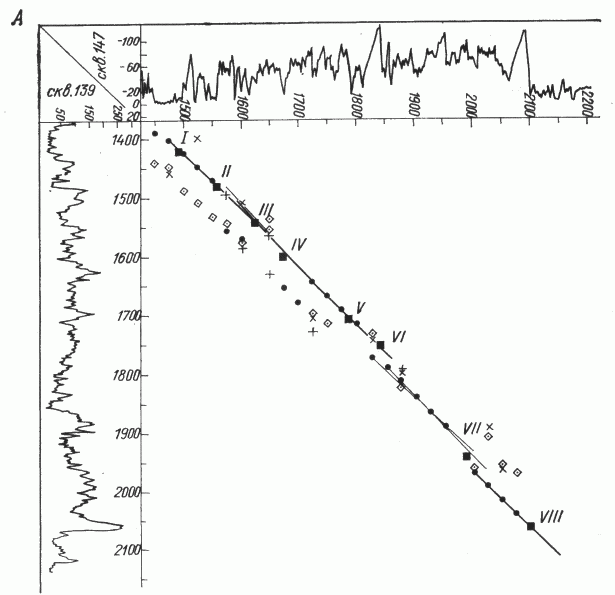
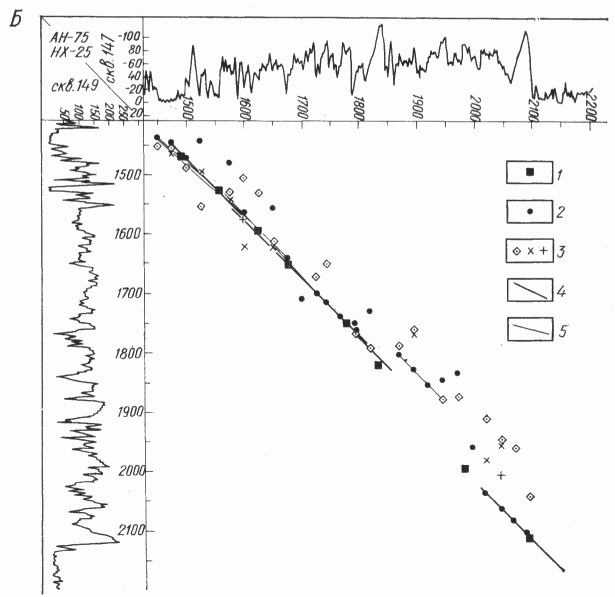
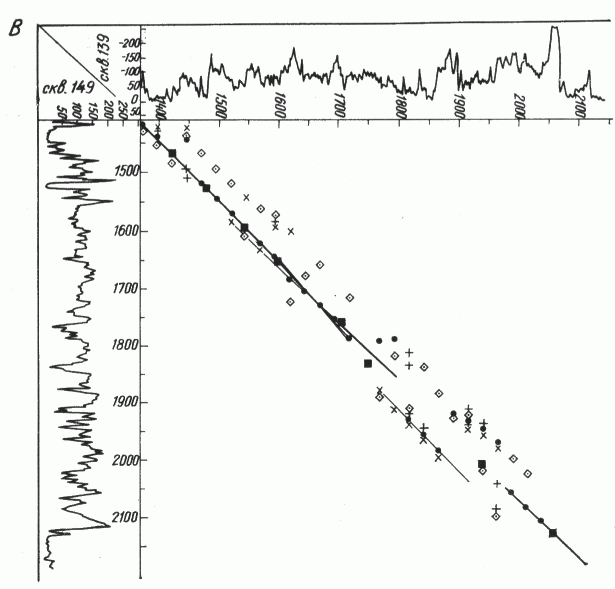
Точки корреляции: 1 - априорные реперов I-VIII, 2 - наиболее сильные (Kмм) для каждого участка корреляции, 3 - следующие по рангу, менее сильные; 4 - отрезки линии корреляции, подтвержденные при тройном сопоставлении парных корреляционных графиков, 5 - прочие варианты корреляции