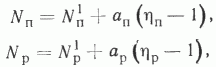
|
УДК 553.98:550.812 |
Влияние темпов работ на количество скважин при поисках и разведке месторождений нефти и газа
Л.Д. КНОРИНГ (ВНИГРИ)
Эффективность поисково-разведочных работ на нефть и газ в значительной мере определяется затратами денежных средств и времени. Поэтому одним из путей ее повышения является сокращение числа бурящихся глубоких скважин. Это обстоятельство, в свою очередь, затрагивает вопрос об определении оптимального количества поисковых и разведочных скважин. Решению его посвящены многочисленные исследования. Осознание того факта, что сокращение числа скважин может быть достигнуто за счет более рациональной системы их размещения, привело к постановке и первому решению оптимизационной задачи с учетом этого фактора [4]. Со временем задача об оптимальном размещении скважин стала рассматриваться в качестве самостоятельной. Появился целый ряд работ на эту тему [1-3 и др.]. В результате в настоящее время достигнуты определенные успехи в ее решении.
Столь пристальное внимание к вопросу о размещении скважин вполне оправдано. Этот фактор является одним из главных (но не единственным), определяющих конечное их число. Не менее важен другой, связанный с зависимым или независимым заложением скважин. Вопрос о том, сколько скважин следует закладывать одновременно, т. е. какими темпами вести работы, что мы выигрываем и что проигрываем, повышая или снижая их, с необходимой строгостью не поставлен. Существующие методы определения оптимального количества скважин не учитывают влияния этого фактора, поэтому к полученным результатам следует относиться осторожно.
В настоящей статье предпринята попытка оценить выигрыш от изменения темпов работ через количество сэкономленных скважин. Решается эта задача путем выявления зависимости числа скважин, затраченных на опоискование единой площади и разведку одного месторождения, от числа одновременно работающих на одном объекте станков (количества одновременно закладываемых, независимых скважин). Существование такой зависимости вытекает из последовательной адаптации поисково-разведочного процесса к накапливаемой информации. Действительно, процесс поиска и разведки протекает так, что заложение последующих скважин корректируется результатами предыдущих. Заложение одновременно большого числа скважин приводит к тому, что частично они оказываются пробуренными не в лучших условиях. Вследствие этого число скважин, необходимых для получения информации в объеме, требующемся для решения задач поиска и разведки, возрастает.
Пусть для выполнения задач опоискования одной площади и разведки одного месторождения необходимо получить о них информацию в объеме соответственно fп и fр. Допустим, что одновременно на месторождении бурится только одна скважина, т. е. опоискование и разведка ведутся одним станком (hп = l и hp=1) и все скважины зависимы. Тогда для того, чтобы получить информацию в объеме fп и fр, потребуется пробурить соответственно Nп1 и Np1 скважин. Если одновременно закладывать по две скважины (hп=2 и hр=2), то для получения информации все в том же объеме fп и fр потребуется уже какое-то другое, но заведомо большее число скважин - Nп2 и Np2. Последнее утверждение (Nп2>Nп1 и Nп2>Np1) следует из того, что местоположение двух одновременно закладываемых скважин в общем случае не совпадет с местоположением двух последовательно заложенных скважин и, следовательно, должно оказаться менее удачным, так как здесь (в отличие от последовательного заложения) местоположение второй скважины не корректировалось данными по первой. Аналогично, если одновременно закладываются три скважины (hп = 3 и hр = 3), то при тех же условиях и для выполнения тех же задач потребуется уже Nп3 и Np3 скважин, причем Nп3>Nп2. Nр3>Nр2. Таким образом, в общем случае количество скважин должно возрастать с ростом числа одновременно закладываемых скважин (числа одновременно работающих станков). В первом приближении в силу отсутствия каких-либо других соображений и недостаточной изученности вопроса рост этот можно считать прямолинейным. Таким образом, рассматриваемые зависимости должны описываться выражениями
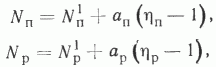
где N1 и а - параметры.
Необходимо определить параметры построенных моделей и оценить адекватность последних действительности.
Сделать это довольно трудно. Ведь нельзя же на одном и том же месторождении проводить, например, разведку несколько раз, сначала закладывая по одной скважине, затем по две т. д., фиксируя каждый раз какое в итоге потребовалось количество скважин. Одним словом, невозможно получить несколько реализаций процесса опоискования и разведки одного месторождения или их группы. Реализация всегда единственна.
В подобных условиях, для того чтобы можно было воспользоваться фактическим материалом, необходимо от реальных объектов, имеющих свои индивидуальные особенности, перейти к некоторым среднестатистическим. Этот переход осуществлялся так, что в качестве исходных данных (число затраченных скважин и число одновременно работающих станков) использовались средние данные по различным районам СССР. В такой ситуации индивидуальные особенности объектов оказывались сглаженными. При этом принималось, что фактический поисково-разведочный процесс в среднем не отклоняется от оптимального. Последнее означает, что если существует линейная зависимость между N и h, то фактические N (средние по районам) будут отклоняться от оптимальных в силу несущественных (не для каждого индивидуального объекта, а для района в целом) причин.
Иными словами, в этих условиях мы имеем дело с совокупностью некоторых среднестатистических объектов, на которых фактически одновременно работало разное число станков. Поиск и разведка проводились по рациональной (при данном числе станков) методике. В итоге из-за разного количества одновременно работающих станков на различных объектах для выполнения задач поисков и разведки потребовалось неодинаковое число скважин. Это число скважин в среднем минимально (при данных f и h).
Тогда можно утверждать, что искомые параметры уравнений будут найдены по
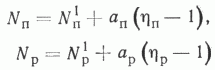
фактическим данным, когда в качестве NПп и hп (соответственно NP и hр) берутся средние данные по районам.
Зависимости Nп от hп и Np от hр, полученные по усредненным данным по районам, показаны на рис. 1. Здесь использованы данные по всем районам СССР за 1971-1975 гг., полученные сектором ресурсов ВНИГРИ.
Для проверки гипотезы линейности изучаемой связи или, говоря иными словами, что модели 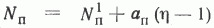 и
и 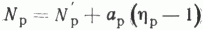 удовлетворительно описывают экспериментальные данные, а также для определения параметров моделей
удовлетворительно описывают экспериментальные данные, а также для определения параметров моделей 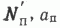 и
и 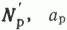 весь диапазон изменений hп и hр был разбит на интервалы. Затем определялось в каждом интервале среднее значение Nп (или NP) и hп (или hр). В дальнейших расчетах использовались только эти значения, что диктовалось необходимостью исключить влияние индивидуальных особенностей объектов.
весь диапазон изменений hп и hр был разбит на интервалы. Затем определялось в каждом интервале среднее значение Nп (или NP) и hп (или hр). В дальнейших расчетах использовались только эти значения, что диктовалось необходимостью исключить влияние индивидуальных особенностей объектов.
Критерием проверки гипотезы линейности изучаемой связи служило отношение выборочных дисперсий
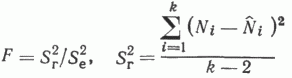
и
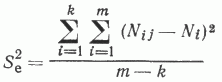
где Ni - среднее значение Nп (или NР) в данном интервале; 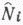 - оценка, полученная по уравнению регрессии, соответствующая среднему значению hi в данном интервале; k - число интервалов; m - число наблюдений
- оценка, полученная по уравнению регрессии, соответствующая среднему значению hi в данном интервале; k - число интервалов; m - число наблюдений 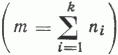 .
.
Если полученное по наблюдениям значение F больше 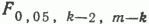 (находится по специальным таблицам), то гипотезу об адекватности модели наблюдениям следует отвергнуть.
(находится по специальным таблицам), то гипотезу об адекватности модели наблюдениям следует отвергнуть.
Параметры уравнений определялись исходя из следующих выражений:
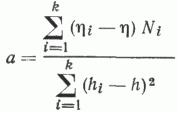
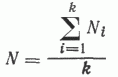
где
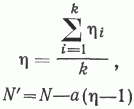
Результаты проверки гипотезы линейности связи N и h представлены в таблице . Они позволяют заключить, что фактические данные не противоречат предположению о возможности описать зависимости Nп от hп и Np от hр с помощью уравнений вида
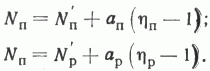
В данном случае получены следующие значения параметров уравнений:

Эти значения параметров модели можно уточнить, учитывая, что продолжительность опоискования (Тп) и разведка (Тр) одного объекта также зависят от числа одновременно работающих на нем станков.
Легко видеть, что T = Nt/h, где t -средняя продолжительность строительства скважины, включая затраты времени на испытание и транспортировку. Подставив вместо N отвечающее ему значение N=N' + а(h-1), имеем:
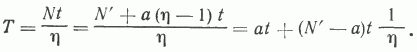
Полученное уравнение является линейным, если в качестве независимой переменной рассматривать величину 1/h. Отсюда следует, что зависимость N/h от 1/h описывается линейным уравнением с параметрами а и N'-а. Результаты проверки гипотезы линейности связи Nn/hп с 1/hп и Np/hp с 1/hр представлены в таблице. Они показывают, что зависимости Nп/hп от 1/hп и Np/hp от 1/hр могут быть удовлетворительно описаны линейными уравнениями. График, демонстрирующий отмеченную связь, представлен на рис. 2 .
При проверке предположения, что рассмотренные выше модели адекватны наблюдениям, а также при оценке параметров моделей использовались средние данные по интервалам, на которые был разбит весь диапазон изменения величины 1/h. Как уже указывалось, это сделано с целью исключить влияние индивидуальных особенностей объектов, на которых проводились поисковые и разведочные работы.
Оценив параметры этих моделей, получили:
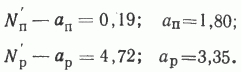
Таким образом, мы имеем по две оценки для каждого параметра уравнений N= N' + a(h-1):
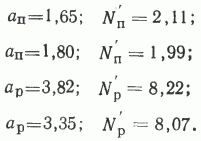
Соответственно каждому значению hп и hp будут отвечать два значения Nп и Np. Очевидно, в качестве оценки этих величин следует брать среднее. Тогда необходимо усреднить и параметры. Окончательно получим
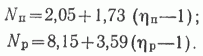
Эти уточненные уравнения и необходимо использовать для определения оптимальных величин.
Из этих же уравнений можно вывести выражения, описывающие зависимость продолжительности опоискования или разведки одной площади (месторождения) от числа одновременно используемых станков. В соответствии с тем, что говорилось выше, имеем:
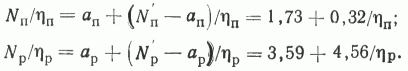
Учитывая, что T=Nt/h, получим:
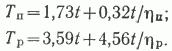
При фактическом по СССР за анализируемый период времени значении t = 1,45 окончательно имеем
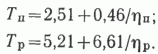
График зависимости продолжительности работ от числа одновременно бурящихся скважин показан на рис. 3 .
Выведенные уравнения связи N с h позволяют предложить новый показатель, характеризующий рациональность зависимого заложения скважин. Этим показателем является отношение a/N'. Если а=0 и тем самым a/N'=0, то величина N не зависит от h, она остается величиной постоянной, равной N'. Иными словами конечное число скважин не зависит от того, бурятся ли все скважины одна за другой, закладываются ли они группами или даже все одновременно. Очевидно, это возможно только в том случае, если местоположение скважин при одновременном их заложении выбиралось настолько удачно, что оно не отличается от расположения скважин, получаемого при последовательном, зависимом их бурении. В этой связи можно утверждать, что чем ближе отношение a/N' к нулю, тем менее можно оправдать зависимое заложение скважин.
Если же отношение a/N'=1, то N растет так же, как и h: если, к примеру, количество одновременно закладываемых скважин увеличить вдвое, то конечное число скважин также увеличится вдвое. Это возможно только в том случае, если, например, из двух одновременно закладываемых скважин только одна способствует выполнению стоящих задач (дает полезную информацию), а вторая совершенно бесполезна - настолько она неудачно расположена. Чем ближе отношение a/N' к единице, тем более оправдано последовательное (одна за другой) заложение скважин. При одновременном забуривании нескольких скважин полезной все равно оказывается только одна, никакого ускорения темпов работ не происходит вследствие неудачного расположения остальных.
Очевидно, что 0<=а/N'<=1. Если бы выполнялось условие a/N'>1, это означало бы, что рост N опережает h, а это возможно только в том случае, когда, например, одна скважина дает больше полезной информации, больше способствует выполнению поставленных задач, чем две одновременно закладываемые. Но практически это исключено, так как из двух одновременно закладываемых скважин местоположение одной совпадает с одной из двух последовательно закладываемых скважин. В нашем конкретном случае получилось
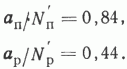
Отсюда видно, что при поисках одновременное заложение нескольких скважин не приводило к сколько-нибудь ощутимому выигрышу, ибо они оказывались неудачно расположенными. Практически из серии одновременно закладываемых скважин на поиски “работала” только одна. А раз только она одна оказывается полезной, то лучшим вариантом было бы последовательное бурение скважин.
При разведке месторождений возникает иная ситуация. Здесь одновременное заложение нескольких скважин имеет смысл, ускоряя темп работ. Получается это потому, что местоположение серии одновременно закладываемых скважин здесь выбирается более удачно. Смысл понятия “более удачно” в данном случае заключается в том, что местоположение большинства скважин совпадает с тем, какое получилось бы при последовательном заложении скважин.
Таким образом, на основании проведенных исследований можно сделать следующие выводы.
1. Число скважин, затрачиваемых на опоискование одной площади (Nп) и разведку одного месторождения (Np), зависит от числа одновременно работающих станков (числа одновременно закладываемых скважин). Эти зависимости в среднем по СССР имеют вид
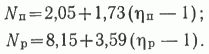
2.При поисковых работах оправдано только зависимое заложение скважин, что перекликается с рекомендациями вести поиски методом одиночных скважин [5]. При разведочных работах, для ускорения их темпа допустимо независимое заложение некоторых скважин.
2.Ускорение темпа поисково-разведочных работ имеет свою оборотную сторону - увеличение числа скважин. Поэтому он не может увеличиваться беспрепятственно, не вызывая роста затрат. Оптимальное количество поисковых и разведочных скважин на одном объекте должно определяться с учетом этого фактора.
СПИСОК ЛИТЕРАТУРЫ
Поступила 20/II 1980 г.
Результаты проверки линейности связи между числом скважин (N) и числом одновременно работающих станков (h), а также между продолжительностью работы на одном объекте (N/h) и величиной (1/h)
|
Этап |
Изучаемая взаимосвязь между показателями |
Число наблюдений m |
Число интервалов k |
Оценки дисперсии |
F0.05 при k-2 и m-k степенях свободы |
Наблюдаемое значение F при k-2 и m-k степенях свободы |
|
|
Sг2 |
Se2 |
||||||
|
Поисковый |
|
173 |
3 |
0,12 |
3,6 |
253 |
30,0 |
|
|
173 |
3 |
0,02 |
1,13 |
253 |
56,5 |
|
|
Разведочный |
|
58 |
4 |
18,01 |
34,77 |
19,47 |
1,93 |
|
|
58 |
4 |
0,62 |
6,97 |
19,47 |
11,24 |
|
Рис. 1. Зависимость числа поисковых (Nп) и разведочных (Np) скважин от числа одновременно работающих на одном объекте буровых станков (h).
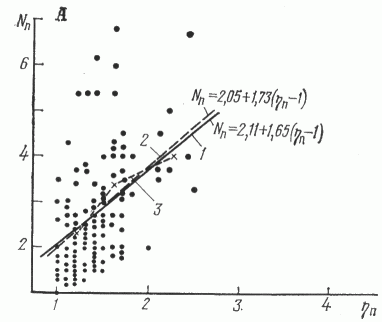
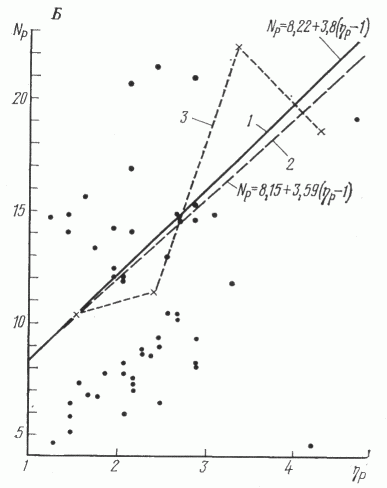
Линия регрессии: 1 - исходная, 2 - уточненная, .3 - эмпирическая. Этапы: А - поисковый, Б - разведочный
Рис. 2. Зависимость отношения числа скважин к числу одновременно работающих буровых станков (N/h) от величины 1/h).
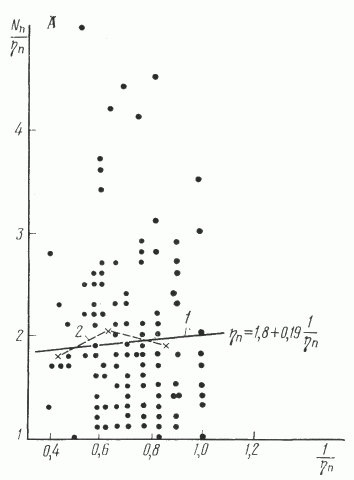
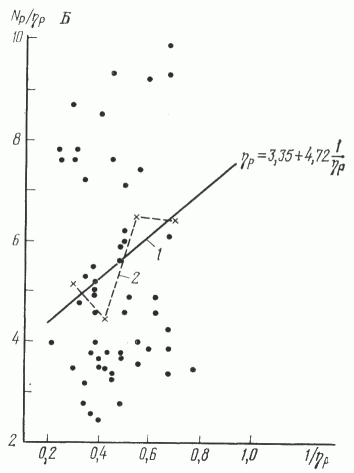
1 - линия регрессии, 2 - эмпирическая линия регрессии. Этапы: А - поисковый, Б - разведочный
Рис. 3. Зависимость продолжительности поисковой оценки одной площади глубоким бурением (Тц) и разведки одного месторождения (Тp) от числа одновременно работающих буровых станков (h).
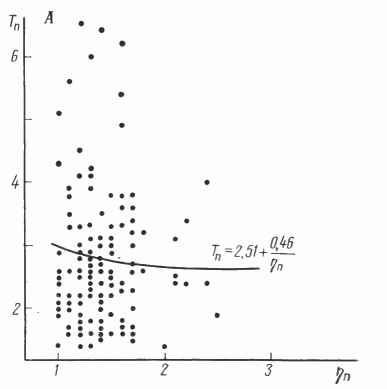
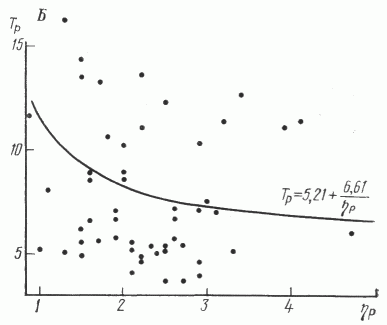
Этапы: А - поисковый, Б - разведочный