Статистические модели структуры и геохимической специализации полей концентраций углеводородных газов
Л.В. ПЕТУХОВ (ВНИИЯГГ), А.И. АНЦЫФОРОВ (ВНИИзарубежгеология)
Широко используемые математические приемы обработки результатов геохимических поисков нефти и газа базируются, прежде всего, на классических разработках теории вероятностей и математической статистики. Учитывая стохастический характер геохимических событий, обработка любой выборки наблюденных (измеренных) значений концентраций предполагает либо знание априори закона статистического распределения, либо его выявление соответствующими приемами. Это условие необходимо, так как выбор соответствующего приема обработки геохимических данных определяется видом их статистического распределения [3, 6, 11].
В многочисленных геологических публикациях [1, 2, 4-10] приводятся сведения о встречающихся в природе распределениях. Последние обычно укладываются в ряд вероятностно-статистических моделей, предельным выражением которых являются нормальная либо отличные от нее (логарифмически-нормальная, гамма и др.) функции плотности распределения (Далее, статистический закон распределения. ).
Высказывались мнения, в соответствии с которыми логарифмически-нормальный закон распределения применительно к распределениям химических компонентов, с одной стороны, является либо статистическим выражением закона действующих масс [12, 13], либо выражением динамического равновесия между диффузионными и конвективными показателями взаимодействующих масс вещества [10], а с другой - свидетельствует об усиленном воздействии главным образом одного из многих факторов накопления - рассеивания химических компонентов [1, 4, 7-9]. В противоположность этому нормальный закон распределения компонента отождествляется с гомогенным распределением химического компонента, отвечающим статистической функции Гаусса. Такой закон характеризует распределение компонента в тех случаях, когда устанавливается равновесие между компонентом и средой, что обусловливает более или менее равномерное распределение компонента по объему геологического объекта [3, 6]. Перечисленные физико-химические явления в конечном счете обусловливают, с одной стороны, структуру и морфологию, а с другой - специфику главных элементов структуры полей концентраций химических компонентов. Поэтому изучение таких явлений имеет важное теоретическое и прикладное значение.
Определенный интерес представляет степень соответствия конкретных видов статистических распределений изучаемых компонентов геохимической специализации главных элементов структуры поля концентраций углеводородных газов - полям нормальных и аномальных концентраций. Применительно к геохимическим поискам залежей нефти и газа в решении этой задачи кроется реальная возможность объективного истолкования природы и механизма формирования полей концентраций на основе статистического анализа структуры полей и соответствующих им законов распределения полеобразующих компонентов в объекте геохимического опробования (представительном или опорном горизонте, геохимическом репере). Однако для этого необходимо знать причины, обусловливающие многообразие распределений. В этой связи авторы проанализировали виды статистического распределения метана в выборках с различным соотношением нормальных (NiН) и аномальных (Nia) концентраций углеводородных газов.
Методика исследования. Для решения поставленной задачи использованы две числовые выборки метана из геологических объектов с диаметрально противоположной геохимической специализацией. Одна выборка (N1) характеризует поле нормальных концентраций метана в карбонатных отложениях сенон-туронского возраста непродуктивной площади Маната, другая (NV) - поле аномальных концентраций в тех же отложениях нефтегазоносных площадей Жетыбай и Тасбулат, причем N1 = Nv =35.
Из N1 и NV были сформированы три промежуточные выборки (NII, NIII и NIV) с различным соотношением NiH и Nia. Эмпирические значения метана для смешанных выборок NII, NIII и NIV подбирались из N1 и NV и группировались в соответствии с заданными процентными соотношениями значений NiH и Nia. Отбор значений из выборок N1 и NV осуществлялся на основе таблиц случайных чисел. Так было сформировано пять типов выборочных данных, расположенных в порядке последовательного уменьшения числа значений NiH от 100 до 0 % и, соответственно - увеличения числа значений Nia от 0 до 100 %. Диаметрально противоположными по геохимической специализации в ряду N1->NV оказались выборки со 100 %-ным набором NiH (тип I, площадь Маната) и Nia (тип V, нефтегазовые месторождения Тасбулат и Жетыбай). Характеристики всех типов выборочных данных приведены в табл. 1 и табл. 2 .
Для каждого типа выборочных значений метана построены полигоны плотности вероятностей ( рис. 1), вычислены среднеарифметические 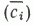 и среднеквадратические
и среднеквадратические 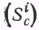 значения концентраций метана, а также значения критерия c2 Пирсона, представляющего собой распределение суммы квадратов нормального распределения величин, у каждой из которых математическое ожидание равно нулю, а дисперсия - единице. Проверка соответствия эмпирического распределения метана теоретическому (параметры последнего определены по данным выборки) осуществлялась путем сравнения вычисленного c2 с табличным
значения концентраций метана, а также значения критерия c2 Пирсона, представляющего собой распределение суммы квадратов нормального распределения величин, у каждой из которых математическое ожидание равно нулю, а дисперсия - единице. Проверка соответствия эмпирического распределения метана теоретическому (параметры последнего определены по данным выборки) осуществлялась путем сравнения вычисленного c2 с табличным 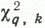 , где q-10 и 5 %-ные уровни значимости для k=r-с-1 степеней свободы при r - числе разрядов группирования выборки и с - числе параметров теоретического закона распределения. За критическую область принимались значения
, где q-10 и 5 %-ные уровни значимости для k=r-с-1 степеней свободы при r - числе разрядов группирования выборки и с - числе параметров теоретического закона распределения. За критическую область принимались значения 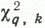 , для которого вероятность c2 <
, для которого вероятность c2 < 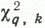 равна вероятности заданного уровня значимости. Если выполнялось неравенство, то считалось, что эмпирическое c2 <
равна вероятности заданного уровня значимости. Если выполнялось неравенство, то считалось, что эмпирическое c2 < 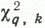 распределение значений метана не противоречит гипотезе о нормальном распределении. Результаты статистической обработки и проверки закона распределения по типам выборочных эмпирических данных приведены в табл. 2 .
распределение значений метана не противоречит гипотезе о нормальном распределении. Результаты статистической обработки и проверки закона распределения по типам выборочных эмпирических данных приведены в табл. 2 .
Результаты исследования. Обработка экспериментальных данных, представленных пятью типами выборочных значений метана, показала, что вид функции его распределения зависит от степени геохимической однородности выборки 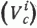 . По данным статистических исследований анализируемые типы выборочных значений метана образуют две группы, достаточно отчетливо различающиеся по виду функции распределения метана.
. По данным статистических исследований анализируемые типы выборочных значений метана образуют две группы, достаточно отчетливо различающиеся по виду функции распределения метана.
Первая группа объединяет предельные случаи встречающихся в природе полей концентраций метана. Попавшие в эту группу выборки удовлетворяют требованиям геохимической однородности (гомогенности): тип I - на 100 % представлен нормальными (VIc = 40%), а тип V - аномальными (VVC = 31,2%) значениями метана. Непротиворечивость распределения выборочных значений метана гипотезе о нормальном распределении в данном случае подтверждается справедливостью неравенства c2 < 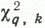 для q, равному 10 и 5 %-ному уровню значимости при k = 1 и 2 степенях свободы (см. табл. 2). Малые значения: крайних в ряду параметров c2 (соответственно 0,85 и 2,98) лишь подтверждают хорошую согласованность экспериментальных данных с соответствующими теоретическими: моделями мономодальных нормальных распределений метана [3, 6]. При кажущемся качественном (видовом) однообразии распределений метана в выборках I и V нетрудно заметить присущие им количественные различия. Достаточно отчетливо они: проявляются при существенных расхождениях значений основных параметров распределения метана, в частности
для q, равному 10 и 5 %-ному уровню значимости при k = 1 и 2 степенях свободы (см. табл. 2). Малые значения: крайних в ряду параметров c2 (соответственно 0,85 и 2,98) лишь подтверждают хорошую согласованность экспериментальных данных с соответствующими теоретическими: моделями мономодальных нормальных распределений метана [3, 6]. При кажущемся качественном (видовом) однообразии распределений метана в выборках I и V нетрудно заметить присущие им количественные различия. Достаточно отчетливо они: проявляются при существенных расхождениях значений основных параметров распределения метана, в частности 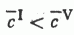 и
и 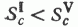 (см. табл. 2 ). Следовательно, в случае гомогенных выборок эти параметры отражают особенности геохимической специализации главных элементов структуры поля концентраций метана, в частности, региональной (нормальной) составляющей поля.
(см. табл. 2 ). Следовательно, в случае гомогенных выборок эти параметры отражают особенности геохимической специализации главных элементов структуры поля концентраций метана, в частности, региональной (нормальной) составляющей поля.
Вторая группа представлена II, III и IV типами выборочных значений метана. По условиям эксперимента указанные выборки отличаются от I и V неоднородностью (гетерогенной структурой) выборочных значений метана (см. табл. 1 , табл. 2 ). Эти особенности выборок фиксируются как повышенными значениями коэффициента вариации метана (55,1<= 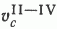 <=86,1), так и специфическими видами присущих ему асимметричных и бимодальных распределений, отличных от мономодальных нормальных, свойственных выборкам первой группы (см. рис. 1). Существенное отличие распределений метана от нормального во второй группе выборочных данных подтверждается невыполнением условия c2 <
<=86,1), так и специфическими видами присущих ему асимметричных и бимодальных распределений, отличных от мономодальных нормальных, свойственных выборкам первой группы (см. рис. 1). Существенное отличие распределений метана от нормального во второй группе выборочных данных подтверждается невыполнением условия c2 < 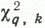 . Большие значения c2(7,13<=c2<=23,46) при тех же уровнях значимости q=10 и 5% и степенях свободы k = 1 и 2, что и в первой группе, а также повышенные значения Vc и Sc (см. табл. 2 ) в данном случае отражают специфичность структурной организации опытных данных, в частности их гетерогенность, обусловленную неодинаковым количественным соотношением значений метана различной природы в выборках рассматриваемой группы.
. Большие значения c2(7,13<=c2<=23,46) при тех же уровнях значимости q=10 и 5% и степенях свободы k = 1 и 2, что и в первой группе, а также повышенные значения Vc и Sc (см. табл. 2 ) в данном случае отражают специфичность структурной организации опытных данных, в частности их гетерогенность, обусловленную неодинаковым количественным соотношением значений метана различной природы в выборках рассматриваемой группы.
Результаты эксперимента позволяют сделать следующие выводы: 1) вид статистического закона распределения и характер кривой дифференциальной плотности распределения устанавливаются по количественному соотношению нормальных и аномальных значений метана в выборке; 2) в случае существенного преобладания (>=75 %) нормальных или аномальных значений метана в выборке (первая группа выборочных данных) наиболее вероятно мономодальное нормальное распределение. При этом вероятность соответствия эмпирического распределения гипотезе о нормальном мономодальном распределении (Рн) будет тем больше, чем однороднее выборка Ni, т.е. при Nia или Nia ->100 % Рн -> 1; 3) при NiН >= 25 или Niа <= 75% (вторая группа выборочных данных) гипотеза о соответствии эмпирического распределения метана нормальному мономодальному распределению отвергается, так как в этом случае более вероятны логнормальное с право- или левосторонней асимметрией и бимодальное распределения как следствие наложения (суперпозиции) двух нормальных распределений метана различной природы - аномального и нормального.
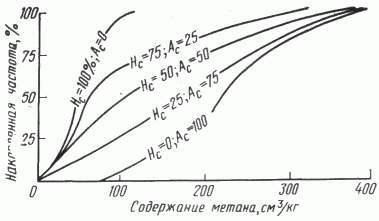
Эти выводы имеют важное прикладное значение. Они могут быть использованы при интерпретации результатов площадных литогазогеохимических съемок. В частности, закон распределения и характер кривой плотности вероятностей полеобразующего компонента, например метана или других углеводородных газов, несет определенную геохимическую информацию о структуре поля его концентраций и, как следствие, о процессах формирования последнего в объекте опробования. В связи с тем, что вид статистического закона распределения и характер кривой плотности вероятностей определяются количественным соотношением нормальных (NiН) и аномальных (Nia) концентраций углеводородных газов в выборке, при интерпретации статистических данных необходимо учитывать условия геохимического опробования, отождествляемого с процессом формирования Ni. Важно, чтобы объект опробования удовлетворял требованиям представительного (или опорного) геохимического горизонта, а плотность опробования последнего была более или менее равномерной в пределах района поисковых работ. Тогда в случае нормального закона распределения углеводородных газов наиболее вероятна относительно гомогенная структура поля концентраций. Последняя будет обусловлена более или менее равномерной встречаемостью в объекте опробования одной из двух разновидностей значений полеобразующего компонента: нормальной или аномальной ( табл. 3 ). Конкретизация геохимической специализации поля концентраций в этом случае может осуществляться путем построения и сравнительного анализа интегральных (кумулятивных) кривых плотности вероятностей, отображающих особенности распределения полеобразующего компонента в пределах исследуемой и эталонных (или продуктивных или “пустых”) площадей, опробованных по одному и тому же горизонту ( рис. 2 ).
Несоответствие встречаемости анализируемого компонента закону нормального распределения свидетельствует о гетерогенной структуре поля концентраций, обусловленной геохимической неоднородностью выборочных значений углеводородных газов, коррелирующихся с координатами местоположения пунктов опробования. Обычно оно указывает на возможность накопления углеводородных газов в пределах отдельных участков опробуемого объекта. Как и в предыдущем случае, специфика структурной организации выборочных данных, характеризующих изучаемое поле концентраций, определяется по табл. 3 и интегральной кривой плотности вероятностей анализируемого полеобразующего компонента (см. рис. 2 ).
В случае кондиционных геохимических съемок, характеризующихся равномерной плотностью наблюдений, процентное соотношение нормальных и аномальных концентраций в выборке, объем которой соответствует общему количеству пунктов пробоотбора в пределах исследуемой площади, может характеризовать соотношение площадей главных элементов структуры поля (нормальных и аномальных) в пределах исследуемого района. При некондиционных съемках такое соответствие не обеспечивается в связи с неравномерной плотностью изучения главных элементов структуры поля концентраций.
СПИСОК ЛИТЕРАТУРЫ
- Вистелиус А.В., Сарманов О.В. Стохастическое обоснование одного геологически важного распределения вероятностей. - Докл. АН СССР, т. 58, № 4. 1947, с. 631-634.
- Волобуев Г.П., Никаноров А.М. Вероятностно-статистическая оценка влияния основных геологических факторов на формирование химического состава подземных вод. - Геология нефти и газа, 1971, № 4 , с. 51-55.
- Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике (общая часть). М., Гостехиздат, 1955.
- Колмогоров А. Н. О Логарифмически- нормальном законе распределения размеров частиц при дроблении. - Докл. АН СССР, т. 31, № 2, 1941, с. 99-102.
- Мидлтон Г.В. Возникновение логнормального распределения частот в осадках. - В кн.: Вопросы математической геологии. М., 1968, с. 37-44.
- Налимов В.В. Применение математической статистики при анализе вещества. М., Физматгиз, 1960.
- Разумовский Н.К. Характер распределения содержаний металлов в рудных месторождениях. - Докл. АН СССР, т. 28, № 9, 1940, с. 815-817.
- Разумовский Н.К. Логарифмически-нормальный закон распределения вещества и его свойства. - Зап. Ленингр. гор. ин-та, т. 20, 1948, с. 105-118.
- Родионов Д.А. К вопросу о логарифмически-нормальном распределении содержаний элементов в изверженных горных породах. - Геохимия, № 4, 1961, с. 324- 328.
- Смирнов С.И. Вероятностно-статистические закономерности распределения химических элементов в природных водах. - В кн.: Гидрохимические материалы. М., 1963, с. 5-55.
- Ястремский Б.С. Некоторые вопросы математической статистики. М., Гостоптехиздат, 1961.
- Coulomb R., Goldstein M., Lemercier M. Etude de la repartition statistique de l'uranium dans les granites. Contribution a la prospection geochimique des grands massifs. - Congreso geologico international, XX session, 1956, Simposium de exploration geoguimica, t. 1, Mexico, 1958.
- Matheron G. Application des methodes statistiques a i'evalution des gisements. Annales des mines, v. 144, decembre, 1955.
Поступила 8/I 1980 г.
Таблица 1
Структура выборочных значений метана
|
Содержание метана (n*10-4 см3/кг) |
Частоты встречаемости (m) значений метана в выборках с различным набором (%) аномальных концентраций (AiC)* |
|
0I |
25II |
50III |
75IV |
100V |
|
0-79 |
29 |
21 |
14 |
8 |
0 |
|
80-159 |
6 |
6 |
9 |
6 |
8 |
|
160-239 |
|
5 |
4 |
9 |
14 |
|
240-319 |
- |
3 |
7 |
7 |
9 |
|
320-399 |
- |
- |
1 |
5 |
4 |
*Индекс (i) при количественном выражении Aс обозначает порядковый номер экспериментальной выборки.
Таблица 2
Характеристика и параметры распределения выборочных данных метана непродуктивной площади Маната и нефтегазоносных объектов Жетыбай и Тасбулат
|
Характеристики выборок
и параметры распределения метана |
Типы выборочных данных |
|
I* |
II |
III |
IV |
V** |
|
Количество экспериментальных данных в выборке N'==NiH + Nia |
35 |
35 |
35 |
35 |
35 |
|
Количество значений в выборке Ni: |
|
|
|
|
|
|
нормальных NiH, % |
100 |
75 |
50 |
25 |
Нет |
|
аномальных Nia, % |
Нет |
25 |
50 |
75 |
100 |
|
Среднеарифметическое значение концентрации с в выборке, см3/кг |
53,80 |
93,66 |
132,14 |
181,60 |
218,86 |
|
Среднеквадратическое отклонение Sc, см3/кг |
21,45 |
80,63 |
100,00 |
100,30 |
68,24 |
|
Коэффициент вариации Vc, % |
40,00 |
86,10 |
75,70 |
55,10 |
31,20 |
|
Количество разрядов группирования r |
4 |
4 |
5 |
5 |
5 |
|
Число параметров теоретического закона распределения с |
2 |
2 |
2 |
2 |
2 |
|
Число степеней свободы k = r -с - 1 |
1 |
1 |
2 |
2 |
2 |
|
Вычисление значения критерия c2 Пирсона |
0,85 |
23,46 |
13,03 |
7,13 |
2,98 |
|
Критические значения критерия c2 Пирсона |
|
|
|
|
|
|
c 2q = 0.10; k |
2,70 |
2,70 |
4,60 |
4,60 |
4,60 |
|
c 2q = 0,05; k |
3,80 |
3,80 |
6,00 |
6,00 |
6,00 |
|
Соответствие эмпирического распределения гипотезе о нормальном распределении |
Да |
Нет |
Нет |
Нет |
Да |
Геохимическая специализация: * поле нормальных концентраций непродуктивной площади Маната; ** поле аномальных концентраций нефтегазоносных площадей Жетыбай и Тасбулат.
Таблица 3
Структура и геохимическая специализация полей концентраций УВ
|
Структура поля концентраций |
Количество нормальных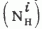 и аномальных и аномальных 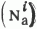 значений в выборке, % значений в выборке, % |
Тип структурной организации поля |
Характеристика статистического распределения выборочных данных (N) |
Геохимическая специализация поля концентраций УВ |
|
Модель |
Параметры** модели |
|
NН |
Na |
|
Гомогенная (нормальная) |
100 |
- |
I |
Нормальная мономодальная |
Рсн>0; Рcа ~ 0; A=0 |
Область развития нормальных концентраций |
|
75-100 |
0-25 |
II |
Логнормальная* с правосторонней асимметрией |
Рсн>Рса>0; А >0 |
Область развития нормальных и аномальных концентраций |
|
Гетерогенная |
50-75 |
25-50 |
III |
Бимодальная* с правосторонней асимметрией |
Рсн > Рса>0; А >0 |
|
25-50 |
50-75 |
IV |
Бимодальная* с левосторонней асимметрией |
Рса>Рсн>0; А <0 |
|
0-25 |
75-100 |
V |
Логнормальная* с левосторонней асимметрией |
Рса>Рсн>0; А <0 |
|
Гомогенная (аномальная) |
|
100 |
VI |
Нормальная мономодальная |
Рса>0; Pсн = 0; А=0 |
Область развития аномальных концентраций |
*Суперпозиция двух нормальных распределений значений сн и са, сн -нормальные, са - аномальные концентрации полеобразующего компонента.
** РcН -частота встречаемости сН; Рa -частота встречаемости сa; А - ассиметрия кривой плотности распределения концентраций полеобразующего компонента с.
Рис. 1. Дифференциальные кривые распределения метана в выборках с различным соотношением Нс и Ас
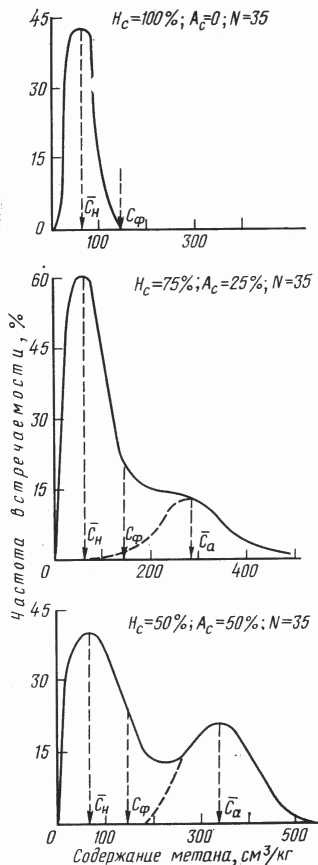
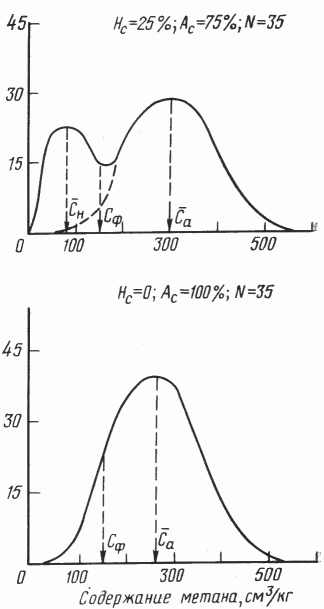
Наиболее часто встречающиеся значения метана: сн - в поле нормальных концентраций (Hс), са - в поле аномальных концентраций (Aс), Сф - верхний предел фоновых концентраций
Рис. 2. Интегральные кривые распределения метана в выборках с различным соотношением Нс и Ac
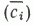 и среднеквадратические
и среднеквадратические 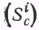 значения концентраций метана, а также значения критерия c2 Пирсона, представляющего собой распределение суммы квадратов нормального распределения величин, у каждой из которых математическое ожидание равно нулю, а дисперсия - единице. Проверка соответствия эмпирического распределения метана теоретическому (параметры последнего определены по данным выборки) осуществлялась путем сравнения вычисленного c2 с табличным
значения концентраций метана, а также значения критерия c2 Пирсона, представляющего собой распределение суммы квадратов нормального распределения величин, у каждой из которых математическое ожидание равно нулю, а дисперсия - единице. Проверка соответствия эмпирического распределения метана теоретическому (параметры последнего определены по данным выборки) осуществлялась путем сравнения вычисленного c2 с табличным 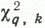 , где q-10 и 5 %-ные уровни значимости для k=r-с-1 степеней свободы при r - числе разрядов группирования выборки и с - числе параметров теоретического закона распределения. За критическую область принимались значения
, где q-10 и 5 %-ные уровни значимости для k=r-с-1 степеней свободы при r - числе разрядов группирования выборки и с - числе параметров теоретического закона распределения. За критическую область принимались значения 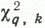 , для которого вероятность c2 <
, для которого вероятность c2 < 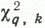 равна вероятности заданного уровня значимости. Если выполнялось неравенство, то считалось, что эмпирическое c2 <
равна вероятности заданного уровня значимости. Если выполнялось неравенство, то считалось, что эмпирическое c2 < 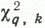 распределение значений метана не противоречит гипотезе о нормальном распределении. Результаты статистической обработки и проверки закона распределения по типам выборочных эмпирических данных приведены в табл. 2 .
распределение значений метана не противоречит гипотезе о нормальном распределении. Результаты статистической обработки и проверки закона распределения по типам выборочных эмпирических данных приведены в табл. 2 .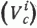 . По данным статистических исследований анализируемые типы выборочных значений метана образуют две группы, достаточно отчетливо различающиеся по виду функции распределения метана.
. По данным статистических исследований анализируемые типы выборочных значений метана образуют две группы, достаточно отчетливо различающиеся по виду функции распределения метана.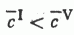 и
и 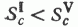 (см.
(см. 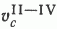 <=86,1), так и специфическими видами присущих ему асимметричных и бимодальных распределений, отличных от мономодальных нормальных, свойственных выборкам первой группы (см. рис. 1). Существенное отличие распределений метана от нормального во второй группе выборочных данных подтверждается невыполнением условия c2 <
<=86,1), так и специфическими видами присущих ему асимметричных и бимодальных распределений, отличных от мономодальных нормальных, свойственных выборкам первой группы (см. рис. 1). Существенное отличие распределений метана от нормального во второй группе выборочных данных подтверждается невыполнением условия c2 < 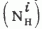 и аномальных
и аномальных 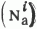 значений в выборке, %
значений в выборке, %

