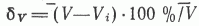 ,
, 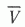 - объем, определенный вручную традиционным методом по данным бурения всех скважин и по данным сейсморазведки и принятый за достоверный,
- объем, определенный вручную традиционным методом по данным бурения всех скважин и по данным сейсморазведки и принятый за достоверный, 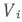 - расчетный объем для i-го варианта расстановки заданного числа скважин.
- расчетный объем для i-го варианта расстановки заданного числа скважин.|
УДК 553.048:553.981 |
О погрешности метода линейной интерполяции при оценке объема сеноманской залежи Уренгойского месторождения
Л.Б. БЕРМАН, В.И. ДМИТРОВСКИЙ, Т.В. НОВИКОВА, О.А. РЕМЕЕВ (ВНИИЯГГ)
Метод линейной интерполяции является одним из основных при составлении карт и оценке на их основе интегральных значений параметров нефтяных и газовых залежей. В частности, он широко применяется для оценок геометрического объема залежей. При этом метод привносит в расчеты определенную погрешность, специально не исследовавшуюся. В табл. 1 приведены данные, характеризующие погрешности составления структурных карт, представленных в ГКЗ СССР, по ряду крупных газовых месторождений. Из табл. 1 следует, что объем информации об изменении рельефа залежи по ее площади в большинстве случаев недостаточен, применительно к требованиям ГКЗ СССР о точности составления структурных карт и предполагаемая погрешность построений сильно отличается от действительной (Нам представляется, что в инструкциях целесообразно лимитировать погрешность восстановления кровли залежи и оценки объема в зависимости от средней мощности. - Прим. авт.). Погрешности карт других параметров еще значительнее [3]. В связи с изложенным было проведено исследование применимости метода в различных ситуациях при оценке геометрического объема сеноманской залежи месторождения Уренгой.
Площадь залежи - несколько тысяч квадратных километров, разбурена она неравномерно, так как подавляющее большинство скважин, пробуренных после подсчета запасов газа в 1970 г., проектировалось на валанжинские отложения. Площадь структуры по валанжинским отложениям меньше, чем по сеноманским, поэтому большинство скважин сосредоточено в центральной и южной частях структуры.
Исследовалось влияние на погрешность метода следующих факторов: степени разбуренности площади; расположения скважин; выбора пар скважин, между которыми проводится интерполяция; вида поверхности параметра (h) над рассматриваемой площадью.
На площади залежи были выделены пять областей ( рис. 1 ), частично перекрывающих друг друга, отличающиеся степенью разбуренности и видом поверхности мощности.
По каждой области проводились оценки геометрического объема с изменяющимся числом скважин и различным их расположением.
В связи с невозможностью обсчета большого числа вариантов вручную рабочим инструментом при проведении расчетов являлась программа, краткая схема работы которой описана ниже.
Задавались координаты М точек на площади залежи и значения мощностей в этих точках. Затем из основного массива М точек, используя стандартный генератор случайных чисел, составлялись комбинации по N точек и для каждой комбинации оценивался геометрический объем залежи. По каждому заданному N проигрывалось несколько вариантов расстановки точек, но любая комбинация из N точек включала постоянную часть, состоящую из точек, задававших границу области и структурную ось.
В качестве процедуры оценки геометрического объема V использовалась программа [1], составленная по следующему алгоритму. Площадь рассматриваемой области триангулируется на заданной системе из N точек, объем по каждому треугольнику вычисляется как объем под поверхностью первого порядка, проходящей через три точки (х1, у1, z1), (x2, y2, z2), (x3, у3, z3), где xi , yi - координаты точек, являющихся вершинами треугольника на площади; zi- - значение мощности h. Полный объем V получается суммированием объемов по всем треугольникам, на которые была разбита область. Таким образом, оценка V основана на использовании метода линейной интерполяции значений мощностей между точками.
Для контроля правильности работы программы [1] были сопоставлены оценки геометрического объема для каждой области. Оценки V вручную по картам, составленным методом изолиний, и по программе расходились в каждом случае не более чем на 1 %.
Для оценки разброса значений V за счет неоднозначности триангуляции для каждой комбинации точек проводилось несколько различных триангуляции, затем оценивалось среднее значение и среднеквадратическое отклонение оценок. При этом установлено, что влияние триангуляции на разброс оценок геометрического объема мало, во всех случаях оно не превышает десятой доли суммарной погрешности оценки объема. При анализе результатов ( рис. 2 ) использовались средние значения V для каждой комбинации точек. В процессе исследования проведено примерно 700 оценок геометрического объема при различном числе точек, их расположении и триангуляции. Результаты расчетов приведены в табл. 2 и на рис. 2 , где 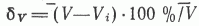 ,
, 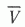 - объем, определенный вручную традиционным методом по данным бурения всех скважин и по данным сейсморазведки и принятый за достоверный,
- объем, определенный вручную традиционным методом по данным бурения всех скважин и по данным сейсморазведки и принятый за достоверный, 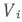 - расчетный объем для i-го варианта расстановки заданного числа скважин.
- расчетный объем для i-го варианта расстановки заданного числа скважин.
Рассмотрение полученных результатов показывает следующее.
Метод линейной интерполяции для Уренгойской структуры при малых N и заданном контуре дает систематически заниженную оценку геометрического объема, что объясняется выпуклостью поверхности мощности. Занижение оценки интегрального значения, полученной с помощью метода линейной интерполяции, характерно для любых поверхностей с преобладанием локальных выпуклостей.
С ростом N оценки стремятся к некоторому асимптотическому значению практически монотонно.
Размах оценок при каждом N (в процентном отношении к минимальной величине V для данного N) достигает 6 %.
Оценки объемов при расстановке скважин геологами при любом N оказываются всегда существенно лучше, чем при случайной расстановке.
Оценка геометрического объема всей сеноманской залежи лишь по результатам бурения является заниженной.
Последнее указывает на необходимость количественного использования данных сейсморазведки для восстановления поверхности залежи и соответственно для оценки ее объема. Необходимость данных сейсморазведки для определения контура залежи следует из результатов расчетов объема области 1 без задания ее границ и оси (см. табл. 2 ).
С тем, чтобы оценить вероятную систематическую погрешность оценки объема сеноманской залежи лишь по результатам бурения, был выполнен следующий анализ приведенных результатов расчетов (см. рис. 2 , табл. 2 ).
Из рис. 2 следует, что величина dV уменьшается с ростом N с различной интенсивностью для областей I и V: для области I dV во всех случаях меньше, чем dV для области V даже при максимальном N. Это обусловлено тем, что средняя величина 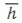 для области I равна 96 м, а для области V - 59 м. Столь значительное влияние величины
для области I равна 96 м, а для области V - 59 м. Столь значительное влияние величины 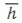 на dV обусловлено тем, что величина площади залежи при расчетах оставалась практически неизменной. Для области I средняя мощность залежи в точках, контролирующих ее контур, равна 60 м, т.е. примерно 2/3 объема контролировалось положением контура. Залежь в области I может быть приближенно представлена как массивная с вертикальными крыльями, т. е. следующим образом ( рис. 3 ): “пьедестал” с
на dV обусловлено тем, что величина площади залежи при расчетах оставалась практически неизменной. Для области I средняя мощность залежи в точках, контролирующих ее контур, равна 60 м, т.е. примерно 2/3 объема контролировалось положением контура. Залежь в области I может быть приближенно представлена как массивная с вертикальными крыльями, т. е. следующим образом ( рис. 3 ): “пьедестал” с 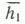 = 60 м и верхняя часть залежи с
= 60 м и верхняя часть залежи с 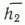 =36 м. При разном N уточняется лишь величина
=36 м. При разном N уточняется лишь величина 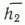 . Если в расчетах объема I области исключить постоянный член, равный
. Если в расчетах объема I области исключить постоянный член, равный 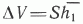 (назовем полученную область Iа), то величины dV по областям Iа и V определяются лишь степенью разбуренности залежи, которая отражается на средней удельной площади Si.
(назовем полученную область Iа), то величины dV по областям Iа и V определяются лишь степенью разбуренности залежи, которая отражается на средней удельной площади Si.
На рис. 4 приведен сводный график зависимости погрешности оценки объема dV от Si по всем исследованным областям залежи, при этом dV характеризует практически систематическую погрешность оценки объема залежи, если Si>50 км2. Из рис. 4 следует, что вид поверхности в плане его влияния на dV практически неизменен в разных частях центрального купола структуры. Значительно более сложной поверхностью характеризуется Ен-Яхинский купол (области III, IV). По рис. 4 можно приближенно оценить вероятную минимальную систематическую погрешность оценки геометрического объема всей сеноманской залежи, если величину V определять лишь по данным бурения. При современном уровне разбуренности структуры вероятная величина систематической погрешности не менее 5 %. В связи с изложенным геометрический объем Уренгойской структуры и ее контур были определены с использованием данных сейсморазведки и бурения.
СПИСОК ЛИТЕРАТУРЫ
Поступила 13/VI 1980 г.
Погрешности восстановления кровли продуктивного горизонта
|
Месторождение |
Объект, горизонт, возраст |
Удельная площадь до начала бурения контрольных скважин Si, км2 |
Среднеквадратическая погрешность прогноза, sH, м |
Систематическая погрешность прогноза |
Характеристика скважин, по которым сделаны оценки h и sH |
|
Газли |
IX |
7 |
10 |
-7,5 |
Эксплуатационные, расположенные преимущественно в своде структуры |
|
XII |
5 |
13 |
-2,5 |
То же |
|
|
Уртабулак |
XV |
1,7 |
42 |
-13 |
Эксплуатационные, равномерно размещенные по площади. По дополнительным разведочным скважинам расхождение фактического и прогнозного положения кровли залежи достигает 100 м |
|
Оренбургское |
Артинско-среднекаменноугольный |
50 |
48 |
-9 |
Разведочные, пробуренные при доразведке месторождения |
|
Уренгойское |
Сеноман |
106 |
31,5*/ 24,5** |
-10/ -7,5 |
То же |
|
Медвежье |
” |
70 |
19,5*/ 15** |
0/ -2 |
Эксплуатационные, пробуренные преимущественно в присводо-вой части структуры |
|
Заполярное |
> |
26 |
6 |
0 |
Разведочные на валанжинские отложения, отстоят от ближайших разведочных скважин менее чем на 4 км |
Примечание. Б - фактические глубины кровли продуктивного горизонта по данным бурения контрольных скважин; П - прогноз глубины кровли продуктивного горизонта до начала бурения контрольных скважин; n - число контрольных скважин: Н - абсолютная отметка кровли. * По скважинам, удаленным от ранее пробуренных на 4 км и более. ** По всем контрольным скважинам.
Характеристика исследованных областей
|
Область |
Средняя мощность, м |
Удельная площадь Si, км2 |
Расстояния между ближайшими точками наблюдений, км |
Минимальный модуль погрешности оценки объема |dV|, % |
||
|
среднее |
максимальное |
минимальное |
||||
|
I |
96 |
22 |
3,3 |
10,6 |
0,8 |
0,2 |
|
Iа |
36 |
38 |
3,3 |
10,6 |
0,8 |
0,5 |
|
I' |
96 |
22 |
3,3 |
10,6 |
0,8 |
16,6 |
|
II |
69 |
57 |
4,3 |
10,6 |
1,4 |
7,4 |
|
III |
35 |
186 |
12,0 |
16,8 |
4,6 |
20,0 |
|
IV |
42 |
146 |
8,4 |
16,8 |
3,2 |
39,0 |
|
IV |
42 |
158 |
8,4 |
16,8 |
3,2 |
30,6 |
|
V |
59 |
71 |
5,5 |
10,6 |
1,4 |
7,4 |
Примечание. Si = S/L, где L-для I области означает общее число скважин, для остальных областей - число скважин внутри контура. I'-область I, обработанная в режиме без границы и оси. IV' - область IV, обработанная вручную.
Рис. 1. Схема расположения исследованных областей.
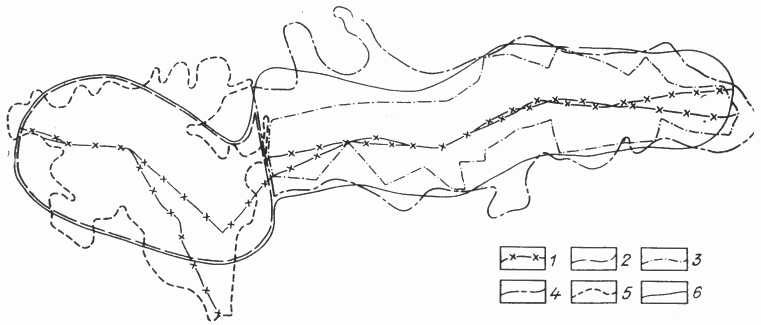
1 - структурная ось; 2 - граница III зоны, 3 -граница I зоны; 4 - граница II зоны; 5 - граница
IV зоны; 6 - граница V зоны
Рис. 2. График зависимости dV от N/Nmax
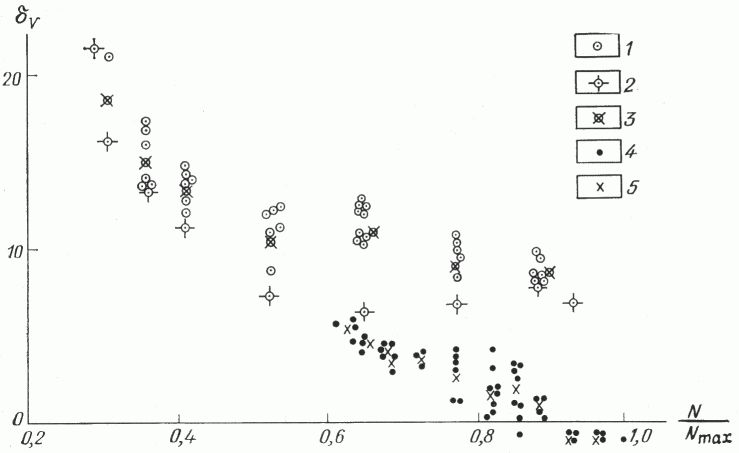
По V области: 1 - значения dV для данного N/Nmax; 2 - значения dV для данного N/Nmax при расстановке точек геологами; 3 - среднее значение dV для данного N/Nmax; по I области. 4 - значение dV для данного N/Nmax; 5-среднее значение dV для данного N/Nmax
Рис. 3. Схема выделения Iа и I областей (в разрезе).
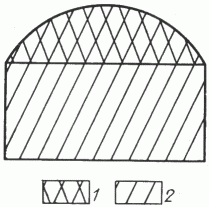
1 - область Iа; 2 - область I (“пьедестал”)
Рис. 4. График зависимости dV от Si (см. также примечания к табл. 2).
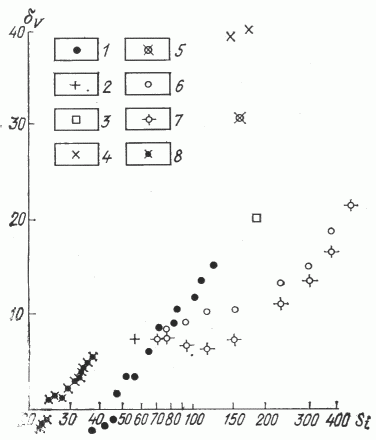
Значения dV по областям: 1 - Iа, 2 - II, 3- III, 4 - IV, 5 - IV, 6 - V, 7 - V при расстановке точек геологами, 8 - I