На первых этапах изучения геологии седиментационных бассейнов для выбора первоочередных объектов поисков важно по минимуму исходной информации оценить хотя бы приближенно начальные геологические и извлекаемые ресурсы (НГР и НИР) УВ. Для этого, как правило, используют различные модификации объемно-статистического метода, основанного на существовании стохастической связи между НГР и полным объемом осадочного выполнения бассейна. Действительно, кажется почти очевидным, что при прочих равных условиях большему объему осадочного выполнения соответствует большая величина НГР.

В простейшем варианте объемно-статистического метода предполагают, что НГР (Q) прямо пропорциональны объему осадочного выполнения бассейна (V):

Q = aV, (1)

где коэффициент а имеет смысл средней плотности НГР УВ в бассейнах и может быть установлен по выборке хорошо изученных нефтегазоносных бассейнов (НГБ).

Одним из первых описал этот метод Уикс [16]. Позднее связь объема осадочного выполнения с НГР анализировали Н.Б. Вассоевич и Г.А. Амосов [3], А. Леворсен [12], В.С. Вышемирский, А.Э. Конторович и А.А. Трофимук [4] и др. М.Ф. Двали и Т.П. Дмитриева [6], вычислив среднее значение удельных запасов (отношение Q к V), определили а для платформенных бассейнов, межгорных впадин и передовых прогибов.

Обобщением первоначального варианта объемно-статистического метода является использование уравнения линейной регрессии Q на V:

Q = bV+c, (2)

где коэффициенты b и с определяются методом наименьших квадратов по выборке хорошо изученных НГБ.

Существуют также модификации объемно-статистического метода, связывающие величину НГР с другими характеристиками осадочного выполнения бассейна. Например, И.И. Нестеров и В.В. Потеряева [14] пришли к выводу, что НГР (Q) коррелируют со средней объемной скоростью осадконакопления W (значение коэффициента корреляции r=+0,92) и привели соответствующее уравнение регрессии:

Q = 3,71 W-6,482, (3)

где Q - НГР, млн. т условных УВ, a W - объемная скорость осадконакопления, км³/млн. лет. Возможны, также модификации с многомерными уравнениями регрессии, учитывающие сразу несколько параметров. Например В.Д. Наливкин, В.С. Лазарев, М.Д. Белонин и др., прогнозируя объемную плотность НГР УВ с помощью уравнений многомерной регрессии, использовали следующие переменные: тектонотип бассейна, объем нескладчатых и слабоскладчатых отложений фанерозоя, максимальную мощность нескладчатых и слабоскладчатых отложений фанерозоя, число мега-комплексов, возраст верхнего мега-комплекса, абсолютный объем мезозойско-кайнозойских отложений и относительный (от всего осадочного выполнения) и т. д. [11].

Цели данной работы, однако, ограничены рассмотрением вариантов оценки НГР УВ на основе эмпирически найденных зависимостей между Q и V, простейшая из которых выражается уравнением (1).

В последнее время в связи с накоплением и уточнением исходного материала по НГБ предпринимались попытки найти более точный вид уравнения регрессии, связывающий Q и V. Для малых межгорных впадин такую попытку сделали А.А. Арбатов и А.В. Кондаков. Изучив материалы по 40 НГБ такой тектонической природы, они нашли, что связь объемов осадочного выполнения с запасами УВ характеризуется значимым коэффициентом корреляции r=+0,65 и описывается уравнением:

lg(Q+1)=2.07+0.87*lg(V+1),

где Q - НГР, млн. т условных УВ, V - объем осадочного выполнения, тыс. км³ [1].

Отметим, что полученная А.А. Арбатовым и А.Б. Кондаковым зависимость связывает НГР и объем осадочного выполнения нелинейным образом.

Существенно более полной информацией при анализе связи НГР и объема бассейна пользовались А.Э. Конторович, М.С. Моделевский и А.А. Трофимук [9]. Была проанализирована выборка из 195 НГБ, для которых достаточно достоверно определены параметры Q и V. Коэффициент корреляции оказался равен 0,73. Обоснованно считая, что такая связь не очень сильна, авторы работы [9] указывают на то, что зависимость между НГР УВ и объемом осадочного выполнения имеет нелинейный характер, и предлагают следующие уравнения для ее описания:

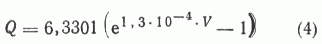
или

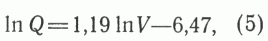
где Q - НГР, млн. т условных УВ, а V -объем осадочного выполнения, тыс. км³.

Как нетрудно видеть, из уравнений (4, 5) следует, что объемная плотность НГР УВ выше для бассейнов с большими объемами. Математически это выражается в виде следующих неравенств:

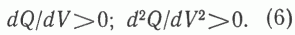
Не исследуя специально причины этого явления, авторы [9] связывают нелинейную зависимость Q от V и вытекающую из нее большую объемную плотность НГР УВ для бассейнов с большим объемом с тем, что в крупных бассейнах к зоне интенсивной генерации нефти и газа приурочена относительно большая доля их осадочного выполнения, чем в микробассейнах.

По современным представлениям о зональности процессов нефтегазообразования в стратисфере, выделяются три зоны генерации УВ: верхняя зона интенсивного газообразования (ВЗГ), главная зона нефтеобразования (ГЗН) и глубинная зона интенсивного газообразования (ГЗГ) [7, 10]. Названные зоны, частично перекрываясь, охватывают фактически весь осадочный чехол. По данным, обобщенным в работах [2, 7, 13], максимум интенсивности нефтеобразования приходится на глубины 2,5-3 км. Приведенные цифры надо рассматривать как ориентировочные, поскольку положение ГЗН в стратисфере зависит от многих факторов и в первую очередь от термической истории отложений и типа ОВ.

Массы газа, генерированные в ВЗГ, могут быть весьма значительны; например, газовые залежи сеномана на севере Западно-Сибирского НГБ образованы газами, генерированными преимущественно в ВЗГ [5]. Однако условия, приводящие к сохранению залежей такого газа, создаются, видимо, довольно редко [8]. Поэтому кажется обоснованным предположение что величина НГР УВ статистически не зависит от объемов пород, которые еще не погрузились на глубины, соответствующие ГЗН. Идею о том, что НГР УВ контролируются объемом осадочных пород, лежащих ниже слоя определенной мощности, в разной форме высказывали многие исследователи. В примечании на с. 576 работы [10] Н.Б Вассоевич и М.К. Калинко пишут: “С нефтегенетической точки зрения к отложениям, генерировавшим в той или иной степени нефть, следует относить лишь те субаквальные осадочные породы, которые залегают на глубинах не менее 2000±500 м...”.

По мнению В.Е. Хаина и Б.А. Соколова, лишь те бассейны нефтегазоносны, мощность отложений в которых более 3 км [15]. Объем осадков, погруженных на глубину более 2 км, включают в список параметров, контролирующих объемную плотность НГР УВ [12]. Если справедливо предположение о том, что величина НГР УВ связана не со всем объемом осадочного выполнения, а лишь с той его частью, которая приурочена к ГЗН и ГЗГ (Vэф) [9], то для прогноза НГР УВ слабоизученных НГБ кажется целесообразным использовать вместо уравнений (1, 2) уравнение линейной регрессии между Q и Vэф:

Q=b*Vэф +c, (7)

где Vэф - эффективный объем осадочного выполнения НГБ, лежащий ниже слоя мощностью e, а коэффициенты b и с определяются методом наименьших квадратов по выборке, содержащей хорошо изученные НГБ.

Величина эффективного объема осадочного выполнения НГБ зависит от мощности неэффективного слоя, связанной, как уже отмечалось, с положением ГЗН в данном НГБ. На основе опубликованных данных о положении в разрезах НГБ верхней границы ГЗН, следует ожидать, что e в различных бассейнах варьирует от 1,5 до 2,5 км.

В качестве геометрической модели НГБ для расчета Vэф было выбрано тело с известной зависимостью площади горизонтального сечения (S) от глубины (h). Если мощность неэффективного слоя равна e, а максимальная глубина НГБ Н, то Vэф можно представить в виде интеграла:

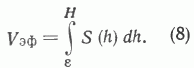
Если имеются структурные карты поверхности фундамента, то S (h) с достаточной точностью можно представить в виде интерполяционного полинома. Однако для проверки предположения о связи величины НГР УВ с эффективным объемом можно воспользоваться более простой и удобной моделью. В качестве S (h) была выбрана достаточно гибкая трехпараметрическая показательная функция:

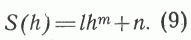
Если допустить, что максимальная мощность осадочного выполнения НГБ достигается лишь в конечном числе точек, то можно записать три очевидных ограничения на вид функции:

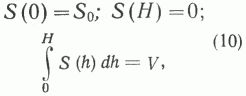
где Н - максимальная мощность, S₀ - площадь дневной поверхности бассейна, V - полный объем осадочного выполнения. С учетом этих условий из уравнений (8, 9) получим следующий вид для Vэф как функции от Н, S₀, V:

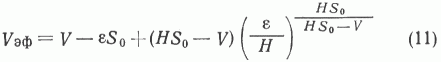
Выражения (6, 11) позволяют, по крайней мере, качественно, объяснить, почему величина НГР УВ растет с увеличением объема быстрее, чем это следует из уравнений (1,2). Действительно, как легко показать, если, подставив выражение (11) в уравнение (17), взять первую и вторую производные, то условие (6) 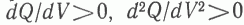будет выполняться.

Таким образом, построенная математическая модель формально обосновывает правильность предположений, сделанных в работе [9].

Для проверки гипотезы о корреляции величин Q и Vэф была сформирована выборка, содержащая 66 НГБ, для которых помимо Q и V были известны H и S₀. Затем для каждого из этих НГБ были рассчитаны в соответствии с уравнением (11) значения Vэф при e=1,5 км; e = 2 км и e = 2,5 км. Для пар Q и V, Q и Vэф (при трех значениях e) были найдены соответствующие парные коэффициенты корреляции. Для Q и V величина коэффициента корреляции (r = 0,75± 0,06) оказалась, естественно, близкой к полученной в работе [9]. А для Q и Vэф при e= 1,5 км, r= 0,89±0,03; при e = 2,0 км, r= 0,87±0,03; при e = 2,5 км, r=0,84 ±0,04.

Отметим, что во всех трех случаях связь между Q и Vэф сильнее, чем между Q и V; все четыре коэффициента корреляции значимы с доверительной вероятностью r=0,999. Существенно, что различия между коэффициентами корреляции для Q и V и для Q и Vэф также значимы. Последнее определенно свидетельствует в пользу предположения о том, что НГР УВ в большинстве НГБ статистически контролируется не всем объемом осадочного выполнения, а лишь его эффективной частью.

Таким образом, на основе введенной в настоящей работе геометрической модели НГБ и современных представлений о зональности нефтегазообразования удалось объяснить нелинейную связь между величиной НГР и объемом осадочного выполнения и подтвердить гипотезу, выдвинутую для объяснения этого факта в работе [9]. Так как статистический анализ выявил, что связь между величиной НГР и эффективным объемом осадочного выполнения сильнее, чем между НГР и полным объемом осадочного выполнения, можно рекомендовать использовать для предварительной оценки НГР на первых этапах изучения нефтегазоносных бассейнов уравнение линейной регрессии, связывающее НГР и эффективный объем осадочного выполнения.

1. Арбатов А.А., Кондаков А.В. Нефтегазоносность малых межгорных впадин. - Геология нефти и газа, 1977, № 11 , с. 66-71.
2. Вассоевич Н.Б. Теория осадочно-миграционного происхождения нефти. Исторический обзор и современное состояние. - Изв. АН СССР. Сер. геол., 1967, № 11, с. 137-142.
3. Вассоевич Н.Б., Амосов Г.А. Геологические и геохимические улики образования нефти за счет живого вещества. - В кн.: Генезис нефти и газа. М., Недра, 1967, с. 5-22.
4. Вышемирский В.С., Конторович А.Э., Трофимук А.А. Миграция рассеянных битумоидов. Новосибирск, Наука, 1971.
5. Геология нефти и газа Западной Сибири / А.Э. Конторович, И.И. Нестеров, Ф.К. Салманов и др. М., Недра, 1975.
6. Двали М.Ф., Дмитриева Т.П. Объемно-статистический метод подсчета прогнозных запасов нефти и газа. Л., Недра, 1976.
7. Конторович А.Э. Геохимические методы количественного прогноза нефтегазоносности. М., Недра, 1976.
8. Конторович А.Э. Генетические принципы раздельного прогноза нефтеносности. - В кн.: Осадочно-миграционная теория образования нефти и газа. М., 1978.
9. Конторович А.Э., Моделевский М.С., Трофимук А.А. Принципы классификации седиментационных бассейнов в связи с их нефтегазоносностью. - Геология и геофизика, № 2, 1979, с. 3-12.
10. Конторович А.Э., Трофимук А.А. Литогенез и нефтегазообразование. - В кн.: Горючие ископаемые. Проблемы геологии и геохимии нафтидов и битуминозных пород. Международный геологический конгресс. XXV сессия. М., 1976, с. 19-30.
11. Критерии и методы количественной оценки нефтегазоносности крупных территорий. Обзор. Геология, методы поисков и разведки месторождений нефти и газа. М., ВИЭМС, 1975.
12. Леворсен А. Геология нефти и газа. М., Мир, 1970.
13. Неручев С.Г. Взаимосвязь между стадийностью нефтегазообразования и размещением нефти и газа в бассейнах. - В кн.: Осадочно-миграционная теория образования нефти и газа. М., 1978, с. 65- 88.
14. Нестеров И.И., Потеряева В.В. К методике оценки ресурсов нефти и газа нефтегазоносных территорий. - Геология нефти и газа, 1971, № 6 , с. 5-10.
15. Хаин В.Е., Соколов Б.А. Современное состояние и дальнейшее развитие учения о нефтегазоносных бассейнах. - В кн.: Современные проблемы геологии и геохимии горючих ископаемых. М., 1973, с. 94- 108.
16. Weeks L.G. Highlishts on 1948 Developments in Foreign Petroleum Fields. - Bull. 1949, v. 33, N 6, p. 1029-1124.

Поступила 24/IV 1980 г.