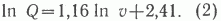
|
УДК 553.048:553.98 |
Метод вероятностной оценки ресурсов нефти и газа седиментационных бассейнов
В.С. РЕЗНИК (ВНИГРИ)
Рассматриваемый ниже метод статистико-генетических моделей (СГМ) оценки начальных потенциальных ресурсов УВ - результат синтеза двух существующих подходов к прогнозу нефтегазоносности: генетического и эмпирико-статистического. С одной стороны, рассматриваются все геологические факторы процесса генерации УВ в соответствии с современной теорией, с другой - рассчитываются численные зависимости и коэффициенты для каждого фактора на основе собранных эмпирических данных о запасах нефти и газа в наиболее разведанных регионах мира путем многомерного регрессионного анализа.
Данный метод от методов сравнительных геологических аналогий отличается тем, что вместо единичного эталона, в какой-то мере сходного геологически, берется эталонная выборка, а вместо довольно субъективно определяемых коэффициентов аналогий используются вычисленные регрессионные зависимости величин ресурсов от наиболее информативных геолого-генетических параметров.
Основное преимущество такого подхода - возможность получения интервальной оценки ресурсов вместо обычной однозначной величины, противоречащей как необходимости прогнозирования в условиях неполной информации, так и современной теории прогностики. В последние годы нефтяники США и Канады переходят к вероятностным оценкам невыявленных ресурсов нефти и газа [13, 15]. Они определяют три критических значения ожидаемой величины: наиболее вероятное, минимальное - практически гарантированное с 95 %-ной и максимально возможное с 5 %-ной вероятностью. Эти значения вычисляются на основе определения экспертами вариативности, учитываемых геологических параметров с последующим суммированием вероятностных оценок по методу Монте-Карло. Предлагаемый метод СГМ обеспечивает получение таких результатов, опираясь на объективные данные общемировой статистики, без привлечения экспертных оценок.
Метод разрабатывался в соответствии со следующими требованиями: 1) методика позволяет постепенно уточнять оценки ресурсов по мере повышения степени региональной изученности, поскольку она представляет собой систему усложняющихся моделей; 2) полный набор генетических факторов, учитываемых моделями на основе современных теоретических представлений, выражается минимальным числом, наиболее общих, независимых и легко оцениваемых (с минимальными погрешностями) геологических параметров; 3) при выборе оптимальных моделей учитывались соответствие формы регрессионных зависимостей основным положениям теорий нефтегазообразования, теснота связи, информативность.
В отличие от миграционных моделей В.И. Шпильмана [9] данный метод ориентирован не на зоны или области нефтегазонакопления, а на бассейны или провинции, к которым может быть применен системный подход. Отсюда разница в классах моделей.
Эталонная выборка. Понятно, что рассчитывать на получение надежных результатов статистических исследований таких сложных природных систем, как седиментационные бассейны, можно лишь при условии системного подхода к анализу взаимодействия факторов, тщательной подборке фактического материала, адекватности и корректности выбираемого аппарата обработки данных [1]. Для получения устойчивых естественных зависимостей потенциала генерации УВ от геогенетических параметров бассейнов эталоны должны соответствовать определенным условиям.
Во-первых, в выборку включались лишь хорошо изученные бассейны, в основном прошедшие пик добычи, у которых доля невыявленных ресурсов мала и, следовательно, оценка начальных потенциальных ресурсов (НПР) УВ имеет минимальную погрешность. Во-вторых, в сумме УВ должны учитываться все компоненты, включая газ, нефть и битумы, возникшие при разрушении залежей, в пересчете на исходную нефть. Это технически сложно, но необходимо для правильной оценки потенциала генерации УВ в залежи. Наконец, рассматриваемые объекты должны быть замкнутыми системами - генерированные ими УВ должны аккумулироваться в их пределах, без обмена с окружающей средой. Иначе искажаются естественные соотношения между геогенетическими характеристиками объектов и фактическими объектами ресурсов. Однако надо учитывать отличия реальных седиментационных бассейнов от идеальных замкнутых систем. Поэтому, прежде чем подходить к НГБ с позиций моделирования, необходимо оценить степень их замкнутости.
Для этого нами был предложен способ оценки замкнутости НГБ [8], учитывающий вероятность вертикальной и латеральной эмиграции УВ. Согласно данному показателю в выборку включались лишь достаточно замкнутые НГБ, а не области преимущественной аккумуляции или же генерации УВ. Пониженные или повышенные значения замкнутости позволяют выявлять объекты с ненадежной прогнозной оценкой.
Перечисленные довольно жесткие требования к эталонам сузили объем выборки бассейнов с 88, по которым были собраны данные, до 40. При этом установлено, что расширение выборки за счет снижения требований к эталонам не улучшает результаты, поскольку уменьшаются надежность и устойчивость получаемых зависимостей. Большую часть выборки составляют хорошо разведанные НГБ США и Канады, где НПР УВ оценивались американскими нефтяниками преимущественно по кривым падения добычи [11-13]. Примерно 1/5 выборки приходится на наиболее изученные отечественные бассейны, по которым использовались материалы последней прогнозной оценки. В остальные вошли отдельные разведанные (не менее чем на 30 %) бассейны Южной Америки, Европы, Ближнего Востока, Юго-Восточной Азии. Здесь ресурсы оценивались комплексом методов [7]. Объемы осадочных пород подсчитывались нами путем измерения площадей изопахит с использованием формулы Симпсона или трапеций.
Объемно-статистические модели. В простейшем случае при минимуме геологической информации о седиментационном бассейне обычно ищут зависимость величины его НПР УВ (Q) от объема осадочного выполнения (v). M.Ф. Двали [2] предложил объемно-статистический метод прогноза нефтегазоносности НГБ, хотя объемные (удельные) плотности и ранее использовались нефтяниками США и СССР [6, 15] для оценки перспектив слабоизученных территорий. Были определены среднеарифметические удельные плотности УВ для НГБ разных тектонотипов. На эти цифры можно было бы ориентироваться при прогнозе в случае нормального, симметричного распределения параметров и значимом различии средних в априорно выделенных подвыборках. К сожалению, такие предположения не подтверждаются при более тщательных статистических исследованиях, что заставляет искать иные зависимости.
На рис. 1 приведена зависимость Q=f(v) в билогарифмическом масштабе, что связано с близостью к логнормальному или показательному закону распределения этих параметров. График показывает, что бассейны трех основных тектонических типов довольно симметрично группируются относительно линии регрессии, общей для всех НГБ, т.е. их средние удельные плотности УВ и дисперсии значимо не отличаются. Попытки применить усложненные классификации бассейнов [5, 13] приводят к неустойчивости средних и увеличению дисперсий в условиях малых выборок.
Более существенным для правильной оценки ресурсов оказывается обоснованный выбор средних плотностей НПР УВ. Так, средневзвешенная плотность 17,7 тыс. т/км3 в 1,5 раза превышает среднегеометрическую 11,2 тыс. т/км3 ( рис. 2 ). Асимметричное, близкое к логнормальному, распределение плотностей НПР УВ показывает, что ни средневзвешенные, ни среднеарифметические плотности не могут рассматриваться как наиболее вероятные при прогнозе. Таковой может служить наиболее часто встречающаяся среднегеометрическая. Поэтому простейшая линейная объемно-статистическая зависимость будет иметь вид
Q= 11,2v. (2)
Более строгая нелинейная зависимость учитывает тенденцию некоторого повышения средних плотностей с увеличением масштабов НГБ:
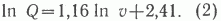
Сходные результаты получены А.Э. Конторовичем и др. [4], хотя и с иными коэффициентами.
Минимальные и максимальные ожидаемые отклонения от наиболее вероятной величины ресурсов при заданном уровне доверительного интервала 0,9 могут быть приближенно вычислены при помощи логарифмического среднеквадратичного отклонения или его отношения к логарифмическому среднему 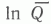 - коэффициента вариации wln:
- коэффициента вариации wln:
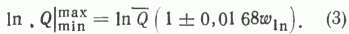
В частности, для линейной зависимости [1] wln =28,1 %, а пределы ожидаемых отклонений удельных плотностей НПР УВ равны 3,3+35 тыс. т/км3. Размах колебаний величины ресурсов, таким образом, охватывает целый порядок, что и характеризует точность простейшей объемно-статистической модели. Для регрессии [2] wln =25,7 %.
Стремление еще уточнить объемную зависимость приводит к мысли, что не вполне правильно рассматривать связь ресурсов УВ со всем объемом осадочного чехла бассейна. Ведь генерирование УВ в заметных масштабах начинается с глубин 1,1-2 км, согласно расчетам разных авторов [3, 10]. Следовательно, правильнее рассматривать лишь потенциально нефтегазогенерирующую толщу (ПНГТ). Надо только обоснованно выбрать ее верхнюю границу с точностью до 1 км. С этой целью на эталонной выборке определялась сила связи величин НПР УВ с объемами пород, залегающих ниже дневной поверхности (1-3 км и т. д.). Наиболее высоким коэффициент корреляции оказался с объемами пород глубже 2 км. Таким образом, удалось уточнить и объемно-статистическую модель:
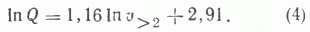
Статистико-генетические модели. На более поздних стадиях геологического изучения территории уже недостаточно ориентироваться только на объем ПНГТ, необходимо учитывать и условия генерации УВ. Даже, не прибегая к теории генезиса нефти и газа, из соображений размерности ясно, что помимо объема ПНГТ нужно учесть содержание в ней исходного ОВ и степень преобразования его в УВ. Поскольку о содержании, типе и распределении ОВ в породах слабоизученных бассейнов известно крайне мало, желательно выразить этот геохимический фактор через геологический, например фациальный (F). Для каждого типа пород среднее содержание и тип ОВ более или менее постоянны, хотя, как показывают тщательные геохимические исследования [6], они все же изменяются с возрастом отложений (t).
Степень преобразования ОВ, как известно, зависит от термобарических условий, а они, в свою очередь, - от глубин залегания (h). Аномальные термобарические условия могут быть учтены специально с помощью поправок. Кроме того, степень преобразования ОВ, по-видимому, зависит и от длительности воздействия, но фактор времени уже включен в модель. Итак, полный набор факторов в модели для ПНГТ: Q= 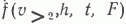 . Они независимы друг от друга с логико-информационных позиций, что и подтверждается весьма слабыми коррелятивными связями, исключая объемы и глубины. Последние требуют совместного учета в форме распределения объемов по глубинам.
. Они независимы друг от друга с логико-информационных позиций, что и подтверждается весьма слабыми коррелятивными связями, исключая объемы и глубины. Последние требуют совместного учета в форме распределения объемов по глубинам.
При изучении связей удельных плотностей НПР УВ (qv = Q/v) с глубинами бассейнов рассматривались не максимальные глубины, как обычно делается, а средневзвешенные, что позволяет учесть влияние объемов пород, расположенных на разных глубинах. Связь между обоими показателями (коэффициент корреляции 0,61) в наиболее простой форме может быть выражена линейной регрессией:
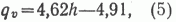
где h - глубина, км; qv - плотность, тыс. т/км3. Однако, линейность, как можно заметить на графике ( рис. 3 ), выдерживается лишь в интервале примерно от 2 до 4 км, а выше и ниже имеет тенденцию к выполаживанию. Поэтому больше подходит к эмпирическим данным и лучше согласуется с теоретическими представлениями [3, 10] логистическая форма зависимости. В соответствии с нею рассчитывались коэффициенты преобразования для разных интервалов глубин, причем не в накопленной, а в дифференциальной форме - так, чтобы единица соответствовала наиболее часто встречающимся плотностям. В интервалах глубин от 2 до 3 км этот коэффициент составляет 0,58, от 3 до 4 км - 1,22 и глубже 4 км - 1,61. В случае упрощенной модели, когда осадочный чехол разбивается всего на две части: от 2 до 3 км и глубже, коэффициенты соответственно 0,6 и 1,55. А для подвыборки высокотемпературных бассейнов, где фиксируются контакты с магматическими породами, или бассейнов, испытавших интенсивные неотектонические поднятия ПНГТ, логистическая кривая смещается в сторону меньших глубин: от 1 до 2 км коэффициент равен 0,33, от 2 до 3 км - 0,86 и глубже - 1,5.
Параметр возраста ПНГТ также рассчитывался средневзвешенным (в млн. лет) по мощностям сводных разрезов для глубин ниже 2 км. Связь между этим показателем и удельными плотностями НПР УВ для тех же глубин сравнительно сильная - коэффициент корреляции 0,69. График показывает ( рис. 4 ), что зависимость близка к линейной:
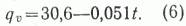
Однако среди молодых бассейнов, преимущественно кайнозойского возраста, разброс увеличивается. Если принять во внимание, что три наиболее верхние точки принадлежат своеобразным высокотемпературным бассейнам с проявлениями вулканизма (Санта-Барбара-Вентура, Оринокский, Центрально-Суматринский), то по остальным намечается тенденция снижения плотностей УВ примерно со 150 млн. лет в обе стороны. Это можно объяснить тем, что молодые осадочные толщи нормальных бассейнов еще не успели достаточно прогреться и степень преобразования ОВ в них невелика [10], а в древних толщах экспоненциально снижается среднее содержание исходного ОВ. Соответственно подобрана более сложная регрессия без учета названных молодых высокотемпературных бассейнов:
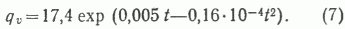
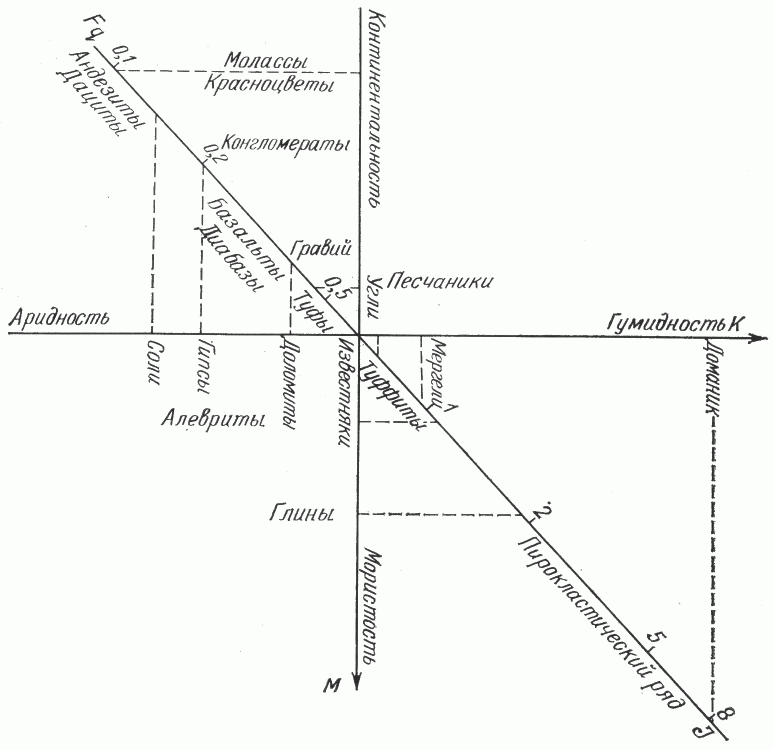
Наибольшие трудности возникли при учете фациального фактора из-за многочисленности фаций и невозможности надежного подбора частных коэффициентов статистическими методами по имеющейся выборке. Установить здесь сколько-нибудь устойчивые зависимости можно только при сведении всего многообразия фаций к минимуму рядов изменчивости. Мы попытались отобразить все фации в трех рядах фациальной изменчивости: уровень осадконакопления относительно поверхности моря М, климатические условия (аридность - гумидность) К и специфичность источника осадкообразования I - пирокластический ряд. Первый ряд содержит терригенные фации от континентальных красноцветов и моласс до глубоководных глин и сланцев, второй - от эва-поритов через карбонатные до угленосных и доманиковых (битуминозных), третий- от кислых трапповых фаций до туффитов с вулканогенами основного состава.
В результате расчета факторных нагрузок по этим трем компонентам фациальной изменчивости в пределах каждого ряда определялись коэффициенты связи фаций (Fq) пород с плотностями НРП УВ (qv). Результаты представлены на трехпараметрическом графике ( рис. 5 ). Причем третья ось I совмещена с осью Fq, на которой в логарифмическом масштабе отложены коэффициенты связи. Поэтому типы пород на оси I непосредственно связаны с численными значениями Fq, а типы пород, расположенные по осям М и К, проектируются на ось Fq для определения соответствующего коэффициента. Общий фациальный фактор для бассейна рассчитывается как средневзвешенный от частных значений по доле объемов различных пород в общем объеме ПНГТ бассейна.
Парный коэффициент корреляции фациального фактора с НПР УВ довольно высок - 0,817. Множественный коэффициент корреляции для всех рассмотренных факторов 0,958. Иначе говоря, лишь около 5 % изменчивости величины ресурсов УВ не контролируется указанными факторами в рамках рассмотренной выборки. Впрочем, большего трудно ожидать, учитывая далеко не абсолютную точность исходных данных.
Для оценки наиболее вероятной величины НПР УВ седиментационных бассейнов с учетом всех рассмотренных факторов можно предложить две основные модели:
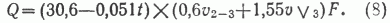
При возрасте ПНГТ в миллионах лет, объемах в миллионах кубических километров, начальные геологические ресурсы УВ получаются в миллиардах тонн. Эта модель не совсем пригодна для нормальных и низкотемпературных молодых бассейнов, возраст ПНГТ которых менее 100 млн. лет, а также для бассейнов, испытавших активные тектонические поднятия и глубокоэродированных. Кроме того, низкотемпературные бассейны платформенных синеклиз с мощностью осадочного чехла не более 4-4,5 км требуют снижения коэффициентов преобразования до 0,5 и 1,1 соответственно градациям глубин. По этой модели wln=7.2 %; сложнее расчет по нелинейной модели:
2.
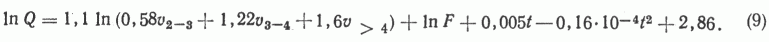
Здесь надо иметь в виду лишь возможность повышения коэффициентов преобразования с некоторым увеличением объема ПНГТ для высокотемпературных бассейнов. По этой модели wln=5,9 %. Не следует забывать, что НПР УВ включают также потери нефти на образование асфальтов и асфальтенов. Это особенно важно учитывать для бассейнов с низкой вертикальной закрытостью. Предлагаемый метод СГМ благодаря системе усложняющихся моделей дает наилучшие результаты, начиная от наименее изученных бассейнов и кончая достигшими максимума добычи нефти и газа.
СПИСОК ЛИТЕРАТУРЫ
Поступила 18/III 1980 г.
Рис. 1. График зависимости НПР УВ от объема осадочной толщи наиболее разведанных нефтегазоносных бассейнов мира.
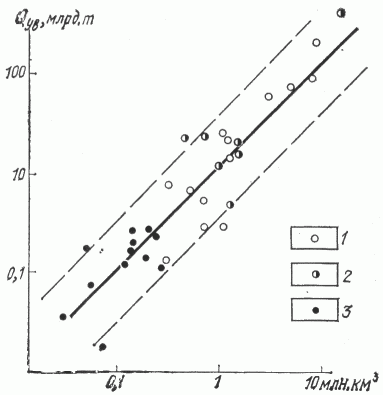
Бассейны: 1 - платформенные, 2 - краевых прогибов, 3 - межгорные
Рис. 2. Гистограмма распределения удельных плотностей ресурсов УВ разведанных нефтегазоносных бассейнов.
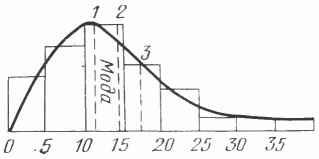
Средние значения плотностей ресурсов УВ (тыс. т/км2): 1 - геометрическое, 2 - арифметическое, 3 - взвешенное
Рис. 3. График зависимости удельных плотностей начальных ресурсов УВ от средневзвешенных мощностей осадочной толщи бассейнов
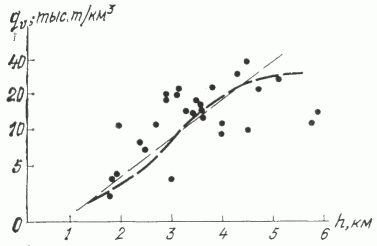
Рис. 4. График зависимости удельных плотностей начальных ресурсов УВ от средневзвешенного возраста потенциально нефтегазогенерирующей толщи (глубже 2 км)
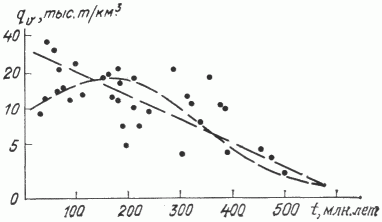
Рис. 5. График связи плотностей ресурсов УВ с фациальными рядами НГБ