В настоящее время пока отсутствуют какие-либо теоретические предпосылки, позволяющие отыскать вероятностный закон распределения пористости, как случайной величины. Поэтому принято считать, что пористость подчиняется либо нормальному закону распределения [1, 5], либо логарифмически нормальному закону [2]. Предлагается также описывать распределение вероятностей пористости как неоднородное, каждая компонента которого подчиняется нормальному закону [5]. Во всех случаях основанием для выбора теоретического распределения пористости является статистическое, изображаемое гистограммой.

Согласно центральной предельной теореме Ляпунова [4], нормальный закон распределения имеет место тогда, когда на случайную величину действует множество факторов, каждый из которых оказывает очень малое влияние. Однако для терригенных отложений нижнего карбона месторождений Башкирии была выявлена достаточно четкая корреляционная связь между пористостью и толщиной песчаников [3]. Аналогичные связи характерны и для девонских песчаников Башкирии. Важно отметить, что пористость существенно увеличивается в зависимости от толщины песчаников. Эти обстоятельства свидетельствуют о том, что нормальный закон можно использовать для описания статистических распределений пористости песчаников только в отдельных случаях.

Неоднородное распределение пористости является следствием резкой литолого-фациальной изменчивости [5] и позволяет дать количественную оценку нескольких типов пород в общем объеме коллектора. Тем не менее иногда оно может быть следствием дефекта статистической совокупности, связанного с непредставительностью исходной информации. Ниже будет показано, что подобные случаи действительно встречаются.

Отмеченные факты свидетельствуют о необходимости еще раз обратиться к анализу фактического материала с целью отыскания нового подхода к выбору закона распределения пористости.

По многим месторождениям Башкирии, приуроченным к терригенным отложениям, накоплен богатый материал по результатам определений пористости образцов песчаника. В табл. 1 приведены числовые характеристики статистических распределений пористости песчаников по основным продуктивным горизонтам терригенного девона и карбона Башкирии.

Из табл. 1 следует, что отрицательное значение коэффициента асимметрии служит характерным признаком статистических распределений пористости. Проверка нормальности последних (их числовые характеристики фигурируют в табл. 1 ) показала, что асимметрия не является случайной [4]. Это свидетельствует о том, что для описания приводимых статистических распределений пористости песчаников нормальный закон неприменим.

Широко известные теоретические законы распределения [4] характеризуются положительной асимметрией. Следовательно, ни один из них также нельзя использовать для удовлетворительного описания статистического распределения пористости песчаников. Однако, если применить простой прием обращения гистограмм, то задача подбора теоретического распределения несколько облегчается.

Будем рассматривать статистическое распределение не самой пористости, а лишь некоторой величины х=a-m, где a-максимальное значение пористости, наблюдаемое в данном случае. Использование этого-приема позволит преобразовать статистическое распределение с отрицательной симметрией в такое же, но с положительной асимметрией.

Анализ обращенных гистограмм пористости показал, что они удовлетворительно описываются широко известным гамма-распределением [4]. Так, на рис. 1 приведена обращенная гистограмма распределения пористости и соответствующая ей теоретическая функция для песчаников залежи I. График указывает на качественную сходимость обращенного статистического распределения пористости и дифференциальной функции гамма-распределения.

Поэтому формально будем искать теоретическое распределение пористости в виде

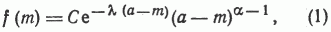
где С - постоянный множитель, а - максимально возможное значение пористости, m - пористость; a, l - параметры распределения.

Здесь значение параметра несколько отличается по физическому смыслу от ранее указанного. Это максимально возможное значение пористости для песчаников конкретной залежи, и оно может быть больше максимального значения, наблюдаемого в имеющейся статистической совокупности. При этом 0<=m<=a.

По условиям нормировки [4], постоянная С определяется как

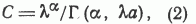
где 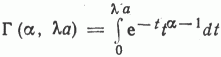- неполная гамма-функция, a t=l(a-m). Подставляя найденное значение постоянного множителя, окончательно найдем:

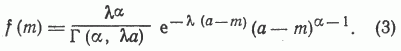
Полученное выражение в первом приближении можно принять в качестве дифференциальной формы закона распределения пористости песчаников.

Установим связь между найденными параметрами (см. уравнение 3) и числовыми характеристиками. Среднее значение пористости (ее математическое ожидание) можно определить, умножая функцию (3) на m и интегрируя полученное произведение от 0 до а. Опуская математические операции интегрирования, приведем окончательный результат:

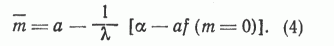
Расчеты показывают, что при m=0 дифференциальная функция распределения (3) имеет значущую цифру в четвертом или даже шестом знаке после запятой. Поскольку значение параметра а по своему физическому смыслу не может быть более 35, то вторым членом в квадратных скобках формулы (4) можно пренебречь ввиду его малости.

Тогда среднее значение пористости можно выразить через параметры распределения по более простой формуле:

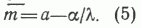
С учетом сказанного дисперсия пористости также может быть найдена с достаточной степенью точности по следующей упрощенной формуле:

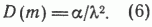
Мода пористости может быть установлена, если взять производную от функции (3) и приравнять ее к нулю. Не проводя элементарных преобразований, напишем сразу выражение для моды.

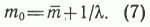
Решая совместно (5) и (6), выразим параметры распределения пористости через числовые характеристики - дисперсию пористости и ее среднее значение.

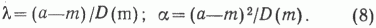
Приводимые формулы (7) и (8) позволяют рассчитать значения параметров теоретического распределения (3) по статистическим значениям дисперсии, моды и средней пористости. Если статистические значения средней пористости и дисперсии устанавливаются однозначно по результатам обработки исходной совокупности значений пористости, то оценка моды вызывает определенные затруднения. Поэтому в первом приближении за статистическое значение моды следует принимать величину пористости, соответствующую средине того интервала гистограммы, который имеет наибольшую статистическую вероятность. При этом желательно интервал изменения пористости принимать равным одному проценту.

По известному среднему значению пористости и выбранному значению моды сначала дается оценка параметру l по формуле (7). Затем по первому равенству формулы (8) оценивается величина параметра а. Если величина этого параметра окажется меньше максимального значения пористости, наблюдаемого в данной статистической совокупности, то значение параметра а выбирают равным максимальному значению пористости плюс один-два процента. Желательно использовать целочисленное значение параметра а, поскольку ошибка в выборе величины этого параметра мало влияет на изменение вида теоретической кривой распределения пористости.

После выбора значения параметра а по формуле (8) рассчитывают окончательно параметры a и l и по формуле (7) находят теоретическое значение моды пористости. Зная теперь параметры распределения, можно по формуле (3) рассчитать его теоретическую функцию.

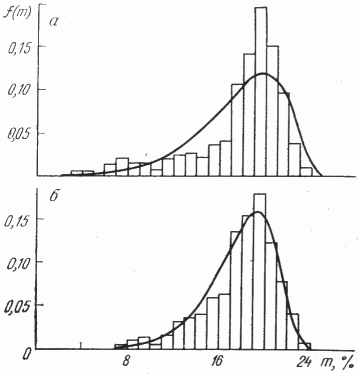
На рис. 2 приведены гистограммы и функции распределения пористости песчаников для залежей IV и VII соответственно (см. табл. 1 ). Как видим, теоретически с помощью формулы (3) можно вполне удовлетворительно описать статистические распределения пористости как девонских, так и угленосных песчаников, хотя характер статистических распределений этих песчаников заметно отличается.

Оценка соответствия теоретического распределения пористости наблюдаемым статистическим по критерию согласия А.Н. Колмогорова в некоторых случаях дает вероятность соответствия, равную 0,1-0,2, если интервал изменения пористости равен одному проценту. При укрупнении интервала изменения пористости до двух-трех процентов вероятность соответствия по указанному критерию повышается до 0,6-0,8. Все это свидетельствует о хорошей сходимости теоретического (3) и статистических распределений пористости песчаников.

Тем не менее в некоторых случаях вероятность соответствия оказывается очень низкой, что вызывает сомнения в правомерности использования предлагаемого теоретического распределения. Так, статистическое распределение пористости песчаников залежи 1, приводимое в обращенной форме на рис. 1, а в обычной форме на рис. 3 , а, практически не подчиняется теоретическому Т (3). По внешнему виду статистическое распределение пористости песчаников этой залежи удобнее рассматривать как неоднородное [5], допуская, что коллекторы представлены несколькими типами песчаников.

Однако анализ исходных данных показал, что в данном случае неоднородность статистического распределения оказывается следствием непредставительности исходной информации. В табл. 2 приведены данные о числе определений пористости по образцам песчаника, взятым из различных участков залежи 1, которые характеризуются интервалами изменения толщины песчаников горизонта D₁.

Как следует из данных табл. 2 , пористость действительно зависит от толщины песчаников, что хорошо согласуется с [3]. Поэтому необходимо, чтобы число определений пористости по образцам было пропорционально доле объема песчаников в соответствующем интервале изменения толщины. Это требование вытекает непосредственно из формулы полной вероятности [4]. Судя по данным табл. 2 , условие пропорциональности не выполнено в последнем интервале, где наблюдается существенный “перебор” образцов. Поэтому часть образцов этого интервала следовало исключить из анализа, что и было сделано. Заметим, что уменьшение числа образцов по интервалам изменения пористости производилось пропорционально вероятности этих интервалов.

Кроме того, анализ исходных данных показал, что значительная часть малопористых непроницаемых образцов получена из кернов, интервал отбора которых перекрывает как песчаники горизонта D₁, так и непроницаемые породы кровли или подошвы. Имеются также непроницаемые образцы, взятые из интервалов, которые по БКЗ, характеризуются как неколлектор. Эти образцы, по-видимому, не отражают емкостные свойства коллектора, по которому подсчитываются запасы, и должны быть исключены при статистической обработке, как непредставительные.

С учетом проведенного анализа исходных данных по залежи 1 было найдено представительное число образцов, а значения пористости по ним были подвергнуты статистической обработке, по результатам которой найдены параметры теоретического распределения пористости. На рис. 3 , б приведены гистограмма и функция распределения пористости песчаников залежи 1, полученные с учетом поправок на представительность исходной информации. При этом вероятность соответствия теоретического распределения статистическому, по критерию согласия А.Н. Колмогорова, равна 0,63.

Заметим, что поправка исходной информации на представительность существенно изменяет числовые характеристики статистического распределения пористости, в том числе и среднее значение последней.

Таким образом, предлагаемое теоретическое распределение пористости достаточно полно описывает статистическое в тех случаях, когда между пористостью и толщиной песчаников существует корреляционная связь. Распределение пористости песчаников может быть близко к нормальному, по-видимому, в том случае, когда толщина песчаников по площади залежи (или по участку) оказывается достаточно выдержанной. Наконец, распределение пористости может быть неоднородным, если на площади залежи имеются зоны с резким отличием литолого-фациальной характеристики песчаников.

1. Ковалев В.С. Изучение неоднородности пласта Б₂ Покровского месторождения. - Труды Гипровостокнефти. 1964, вып. VII, с. 55-68.
2. Комаров В.Л. Определение средней пористости объекта по данным выборочного метода. - Труды УфНИИ, 1961, вып. VIII, с. 218-236.
3. Комаров В.Л. Статистическая оценка коллекторских параметров песчаных пластов. - Труды УфНИИ, 1961, вып. VIII, с. 237-249.
4. Румшиский Л.З. Элементы теории вероятностей. М., Наука, 1970.
5. Саттаров М.М., Андреев Е.А. О функциях распределения коэффициента пористости в терригенных породах девона Башкирии. - Геология нефти и газа, 1966, № 3 , с. 49-52.

Поступила 24/III 1981 г.

Таблица 1

Таблица 2

Рис. 1. Обращенная гистограмма и функция распределения пористости песчаников залежи I

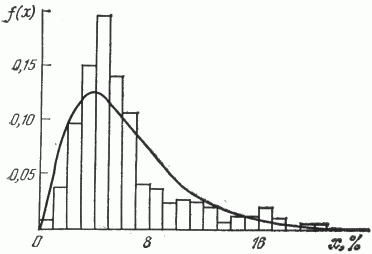
Рис. 2. Гистограммы и функции распределения пористости песчаников горизонта D_IV залежи IV (а), пласта C_VI залежи VII (б)

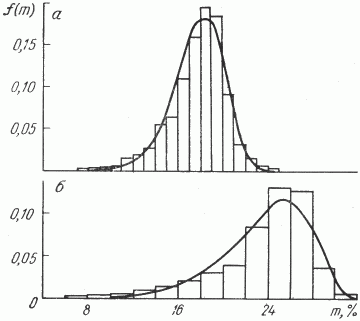
Рис. 3. Гистограммы и функции распределения пористости песчаников горизонта D_I залежи I по фактическому объему исходной информации (а) с учетом поправок на представительность исходной информации (б)