Совершенствование планирования геологоразведочных работ на нефть и газ все более настоятельно требует применения экономико-математических методов анализа и прогноза основных показателей, характеризующих работу организаций и отрасли в целом. Среди этих показателей особое место занимает эффективность глубокого бурения на нефть и газ, т. е. удельный прирост того или иного вида УВ на 1 м проходки. Научно обоснованный прогноз эффективности глубокого бурения на год, а тем более пятилетку позволяет успешно решить две важнейшие задачи планирования геологоразведочных работ на нефть и газ:

• определение объемов глубокого бурения, необходимых для выполнения заданных планов приростов запасов УВ промышленных категорий производственными геологическими объединениями (ПГО) и отраслью в целом;
• определение приростов запасов УВ промышленных категорий для ПГО и отрасли в целом, исходя из оценки производственных мощностей, выражаемых реально выполнимыми объемами проходки.

К настоящему времени предприняты попытки создания методических приемов количественного прогнозирования эффективности глубокого бурения на нефть и газ, отражающих различные подходы к решению этой проблемы. В частности, предложен способ прогнозирования эффективности глубокого бурения(Методика прогнозирования эффективности поисково-разведочных работ на нефть и газ / Н.А. Еременко. Н.А. Крылов, Ю.С. Кувыкин, В.В. Стасенков. - Геология нефти и газа, 1979, № 1, с. 7-13.), основанный на доказанном авторами положении об универсальном для всех нефтегазоносных провинций характере зависимости эффективности глубокого бурения от степени их разведанности. Несомненно, что результаты такого прогноза эффективности могут быть с успехом использованы при выборе стратегии геологоразведочных работ на нефть и газ и перспективном их планировании.

Однако методические приемы, предложенные этими авторами, не решают задачу прогноза эффективности при годовом и пятилетнем планировании, поскольку требования к точности прогноза на этот период существенно выше, чем это может быть обеспечено указанными приемами.

В настоящей работе предпринимается попытка установления количественной зависимости эффективности разведочного бурения на нефть (а_р) от основных факторов, ее определяющих. Здесь под а_р понимается отношение прироста запасов нефти категории C₁ (Qp), полученного при разведке открытых месторождений, к затраченному объему разведочного бурения (h): a_p = Q_p/h.

Заметим, что некоторое количество запасов нефти категории C₁ подготавливается в процессе открытия новых месторождений поисковым бурением. Таким образом, общий прирост запасов, выполняемый той или иной организацией (Q), складывается из прироста запасов, полученного разведочным бурением на ранее открытых месторождениях и на месторождениях, вновь открытых поисковым или опорно-параметрическим бурением (Qп), Q = Q_P+Q_п.

Очевидно, что Q_п гораздо меньше поддается прогнозированию, чем Qp. К тому же для ряда крупных организаций и прежде всего Главтюменьгеологии доля прироста запасов, подготовленных поисковым бурением на порядок меньше доли запасов, подготовленных разведочным бурением.

Именно эти соображения и обусловили выбор сформулированной выше задачи в качестве первоочередной. Прогнозирование же эффективности поискового бурения представляет собой самостоятельную задачу.

Ниже приводится способ математического моделирования процесса подготовки запасов нефти категории С₁ на открытых месторождениях.

Предположим, что в течение некоторого периода времени (1 год) необходимо разведать группу нефтяных месторождений, содержащих суммарный запас нефти категории C₁ равный Q. Вследствие неоднородности геологических условий удельный прирост запасов на 1 м проходки разведочного бурения изменяется как от месторождения к месторождению, так и в пределах одного месторождения

Условно разобьем площадь всех разведываемых месторождений на n участков, каждый из которых содержит одинаковое количество запасов DQ. Будем считать, что эти участки настолько малы, что в пределах каждого из них удельный прирост запасов - величина постоянная

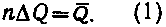
Обозначим удельный прирост на i-ом участке через 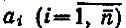, при этом допустим, что участки пронумерованы в порядке убывания удельных приростов. Закон измерения величины a_i в зависимости от номера участка i в пределах одного месторождения довольно сложен. Заметим, однако, что предполагается сквозное упорядочение участков по удельным приростам на всех разведываемых месторождениях, что дает основание считать эту зависимость в первом приближении линейной, так как “спады” и “выполаживания” кривых, описывающих законы для каждого месторождения взаимно гасятся в кривой, отражающей суммарную зависимость. Таким образом, можно предположить, что а_i линейно убывает с возрастанием номера участка i.

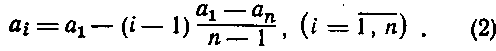
Подчеркнем, что мерой адекватности принятого линейного упрощения является качество аппроксимации реальных данных выведенными ниже зависимостями.

Изложенные допущения эквивалентны ранжировке месторождений или отдельных участков по удельным приростам запасов, т.е. процедуре, в неявном виде почти всегда выполняемой геологами при планировании размещения объемов глубокого бурения и приростов запасов УВ. Естественно, что планируемые объемы разведочного бурения размещаются прежде всего на участках с самыми высокими удельными приростами. Практика планирования допускает некоторые отклонения от этого принципа, что не мешает считать его основополагающим и универсальным.

Исходя из принятых предположений, определим зависимость Q_p от h.

Пусть запланировано h метров разведочного бурения, достаточного для разведки k участков (k<n). При выполнении этих объемов будет подготовлено Q_p (h) = kDQ запасов, откуда

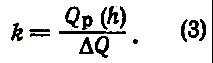
Допустим, что за плановый период будет пробурено h+Dh метров разведочного бурения, причем объем Dh не превосходит объема проходки, необходимого для полной разведки участка с номером k+1, и будет использован именно на этом участке.

Величина разведанных запасов в этом случае составит

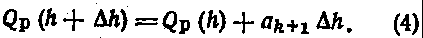
Выразим а_k+1 (удельный прирост запасов на участке (k+1) через Qp(h), используя формулы (1)-(3):

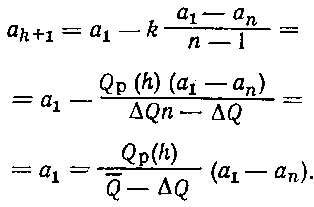
Выбрав число n достаточно большим, мы можем пренебречь слагаемым DQ в знаменателе. Тогда

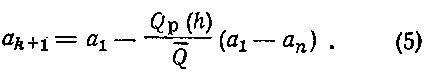
Таким образом, формула (4) с учетом (5) будет иметь следующий вид:

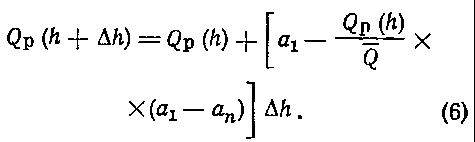
Преобразовав формулу (6), получим уравнение в конечных разностях:

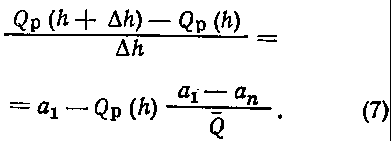
Уравнение (7) при Dh ->0 представляет собой обыкновенное линейное дифференциальное уравнение относительно Q_p (h).

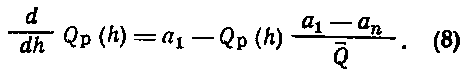
Общее решение такого уравнения можно записать так:

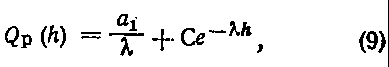
где 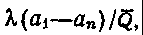, С - константа интегрирования.

Для определения значений параметров в формуле (9) обратимся к их геологическому смыслу и рассмотрим предельный случай:

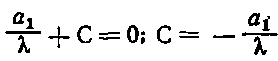
Уравнение (9) при этом принимает вид:

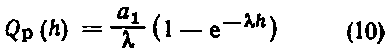
или

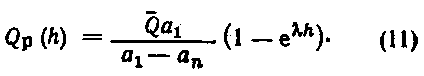
Практически разведка месторождений нефти ведется и на таких участках, в пределах которых удельные приросты запасов близки к нулю. Поэтому, полагая a_n = 0, получим

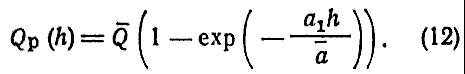
Можно считать, что суммарные запасы промышленных категории разведываемых месторождений пропорциональны их запасам категории С₂ открытых месторождений

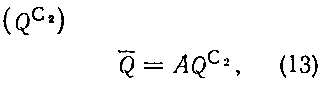
где А - коэффициент пропорциональности. С учетом (13) формула (12) примет вид:

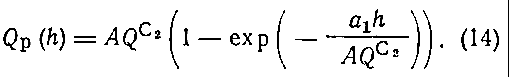
Разделим уравнение (14) почленно на h и введем обозначение:

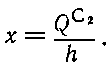
По определению отношение 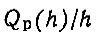(левая часть формулы (14) представляет собой эффективность разведочного бурения. Поскольку ее правая часть зависит только от переменной х, обозначим эффективность разведочного бурения а_p (х), тогда

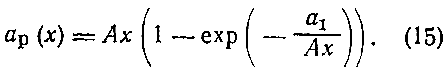
Переменная величина x характеризует обеспеченность 1 м проходки разведочного бурения в планируемом году имеющимися на начало этого года запасами нефти категории C₂.

Параметры А и a₁ формулы (15) целесообразно определять исходя из анализа ретроспективных данных об эффективности разведочного бурения за период, в течение которого геолого-экономическая ситуация оставалась в принципе стабильной. Использование ретроспективных данных возможно при отсутствии резких изменений эффективности, связанных с началом или завершением больших объемов работ на месторождениях, где эффективность разведочного бурения значительно превосходит среднюю для данной нефтегазоносной области или провинции на настоящем этапе ее освоения.

Таким образом, коэффициенты А и а₁ могут быть определены па основе аппроксимации реальных ретроспективных данных в классе функций вида (15) по методу наименьших квадратов.

Рассмотренная выше математическая модель экспериментально использовалась для прогноза эффективности разведочного бурения по Главтюменьгеологии на одиннадцатую пятилетку.

В ходе расчетов было показано, что наилучшая аппроксимация фактических данных достигается в тех случаях, когда аргумент х формулы (15) заменяется аргументом 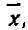определяемым следующим выражением :

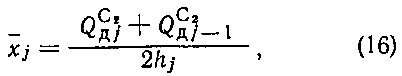
где 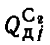- так называемые динамичные запасы нефти категории С₂ на начало j-ro года, h_j - объем разведочного бурения в j-ом году.

Под динамичными запасами категории С₂ понимаются такие запасы, которые по степени их достоверности геологическим и технико-экономическим условиям могут быть в результате разведочного бурения переведены в категорию C₁. Для условий Главтюменьгеологии - это прежде всего запасы категории С₂ крупных месторождений.

Замена аргумента в формуле (15) соответствует тому факту, что за плановый год выполняется разведка лишь части месторождений, открытых к его началу. Остальные месторождения разведываются в течение следующих лет, что приводит к возникновению временного сдвига. Для Главтюменьгеологии этот сдвиг составляет примерно полгода, что отражено в формуле (16).

Среднеквадратическое отклонение расчетных значений эффективности разведочного бурения от фактических за четыре года десятой пятилетки составило менее 5 % среднего значения этой величины.

Таким образом, задаваясь значениями объемов разведочного бурения на определенный плановый период, а также оценив изменения динамичных запасов нефти категории С₂, можно с использованием предложенной математической модели прогнозировать эффективность разведочного бурения на нефть, например для Главтюменьгеологии. Прогнозирование эффективности разведочного бурения для некоторых производственных организаций может быть основано на этой же математической модели, но требует некоторого ее специфического видоизменения.