На этапе разработки перспективного плана отрасли на пять, десять и более лет одной из основных задач является наиболее рациональное распределение ресурсов между объектами планирования (нефтедобывающими объединениями, нефтеносными районами и т. п.). Важное место занимает распределение капиталовложений в разведочном бурении. Это связано прежде всего с двумя обстоятельствами: во-первых, с высокой капиталоемкостью разведочного бурения, во-вторых, с тем, что значительные объемы нефтедобычи при долгосрочном планировании относятся на счет еще не открытых месторождений.

Поэтому правильное распределение капиталовложений в разведочном бурении для каждого объекта планирования приобретает весьма существенное значение и во многом определяет перспективный план добычи нефти.

В последнее время появился ряд работ [1, 2, 3], посвященных проблеме оптимального перспективного планирования разведки запасов нефти. В большинстве из них, как, например, в работе [1], эта задача решается в следующей постановке: при заданном объеме прироста запасов по региону (по стране) DW и за заданный период планирования Т найти такое распределение прироста по объектам DWi, которое обеспечивает минимум капитальных затрат, т. е.

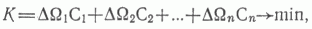
где Ci - удельные капитальные вложения в глубокое разведочное бурение в i-м объекте.

Следует отметить, что в такой постановке не учитываются ограничения на максимально возможный прирост объема бурения по каждому объекту, обусловленный имеющейся материально-технической базой и ее возможным развитием за установленное время планового периода. Поэтому решение такой задачи имеет ограниченное применение, так как может оказаться, например, что всю разведку необходимо вести в одном районе с максимальной эффективностью, а в других районах ее прекратить.

Более полной является следующая постановка: при заданном приросте объема запасов DW найти такое их распределение по районам DWi, при котором обеспечивается минимум капитальных вложений за период планирования при условии, что прирост объема бурения по районам DL_i ограничен, т. е.

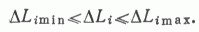
Эта задача, как и задача в работе [3], является типичной задачей нелинейного программирования (учитывая нелинейный характер зависимости DWi(DL_i)).

В такой постановке задача была нами решена численным методом Розенброка [4]. Выбор этого метода обусловлен тем, что он, как известно, обеспечивает “хорошую” сходимость в случае ограничений в виде неравенств.

Алгоритм Розенброка, как и большинство алгоритмов решения задач нелинейного программирования численным методом, не обеспечивает нахождения глобального экстремума. Однако можно показать, что если зависимость L_i(Wi), обратная выбранной зависимости DWi(L_i), выпуклая (как, например, в случае зависимости 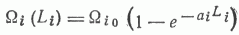предлагаемой многими авторами), то рассматриваемая задача является задачей выпуклого программирования и имеет единственный экстремум. Действительно, легко видеть, что, например, для приведенной экспоненциальной зависимости обратная функция L_i (Wi) имеет диагональную положительную полуопределенную матрицу Гессе, ограничения задачи линейны и, следовательно, решение будет единственным.

Численная реализация задачи была осуществлена на примере разведочных площадей Волго-Урала на ретроспективном материале за 1971-1976 гг. В качестве планового прироста запасов DW использовался фактический прирост за эти годы по региону. Искалось такое распределение объемов бурения по районам, которое обеспечивало бы минимум суммарного объема бурения за эти годы по всем районам при безусловном выполнении плана по приросту запасов по региону. В результате было получено решение, при котором суммарный объем бурения по региону в целом оказался на 13 % меньше фактического. Уменьшение капитальных вложений на 13 % было достигнуто за счет более рационального распределения объемов бурения по объектам разведки.

Следует отметить существенный недостаток описанных выше постановок задачи, а именно то, что весь период планирования рассматривается как один шаг и остается неясным, как должны реализовываться полученные приросты объемов бурения DL_i (и, следовательно, капитальные вложения) внутри интервала планирования.

Более полной и имеющей практическую ценность является постановка, в которой ограничения на объемы бурения и приросты запасов (планы) задаются как функции времени, как это сделано, например, в работе [2]. Анализ решения показал, что при больших периодах планирования (10- 15 лет) и большом числе рассматриваемых объектов разведки (около 30) для получения численного решения требуются весьма значительные затраты машинных ресурсов. В связи с этим было предложено полученные в результате решения второй задачи оптимальные объемы бурения за период планирования распределить во времени в соответствии с выбранной (с точностью до параметров) функцией времени. Пример. Пусть задан период планирования Т лет. В результате решения задачи получили, что по каждому i-му району необходимо реализовать DL_i объем бурения. Предположим, что годовой объем бурения линейно нарастает во времени, т. е. имеет вид

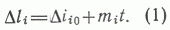
Имея годовой объем бурения Dl_i0 в начале периода планирования, можно определить неизвестный параметр m_i:

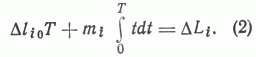
Вычислив m_i из формулы (2), получим годовой объем бурения в течение периода планирования по каждому району. Зная зависимость DW_i(DL_i), легко определить годовой прирост запасов по соответствующим годам и районам. Подбирая вид функции (1), можно получить набор планов Dw_i(t) и Dl_i(t) и выбрать наиболее подходящий.

Этот подход свободен от недостатков первых двух постановок и требует значительно меньше машинных ресурсов, чем решение задачи в работе [2]. Вместе с тем решение получается хотя и оптимальным, но менее общим, чем в задаче из работы [2], так как заранее задан класс функций, в котором ищется решение. Такой подход, вероятно, особенно может быть полезен на предварительных этапах разработки перспективного плана.

В заключение отметим, что использование различных моделей при составлении планов не отрицает, а предполагает участие планового работника (эксперта) в этом процессе. Действительно, любые модели не учитывают и не могут учесть все многообразие реальных условий, таких, например, как освоенность геологического района (наличие дорог, источников энергии и т. д.), наличие или отсутствие квалифицированной рабочей силы и т. п. Поэтому любое полученное на модели решение должно корректироваться экспертом с учетом дополнительных условий, отсутствующих в модели.

1. Баймухаметов К.С., Саттаров М.М. Об одной вероятностно-статистической модели прогнозирования прироста запасов нефти. - Геология нефти и газа, 1975, № 3 , с. 27-32.
2. Баласанов В.А., Каменецкий С.Г. Оптимальное перспективное планирование добычи нефти с учетом подготовки запасов. - Нефт. хоз-во, 1980, № 6, с. 62-64.
3. Селицкий А.Г. Прогнозирование оптимальных объемов геологоразведочных работ на нефть. - Геология нефти и газа, 1978,№ 11 , с. 10-14.
4. Д. Химмельблау. Прикладное нелинейное программирование. М., Мир, 1975.