К оглавлению

УДК 553.982:550.812.1

Оптимизация стратегии поискового бурения на нефть

Л.П. ГУЖНОВСКИЙ (МИНГ), С.Е. КАЗАКОВ (ВНИИКТЭП)

Основная цель поисковых работ заключается в максимизации прироста запасов перспективных категорий с наименьшими затратами на их проведение. При этом выработка наилучшего планового решения предполагает оптимизацию минимум по двум критериям. Эффективных методов решения таких задач до настоящего времени не разработано. На практике в подобных ситуациях прибегают к скаляризации целевой функции - из множества критериев выбирают один (важнейший), а остальные вводят в состав ограничений задачи.

В рассматриваемом случае возможны две постановки однокритериальных задач: 1) добиваться максимальной результативности работ, например, наибольшего прироста запасов по категории С2 (и частично С1 ) при заданном объеме выделяемых для этого ресурсов (затрат), 2) минимизировать затраты для получения заданных результатов поисковых работ (прироста запасов). Решить поставленные задачи - значит определить оптимальное число структур, вводимых в поисковое бурение, установить их очередность, число поисковых скважин, закладываемых на каждой структуре, и т. д. В настоящее время эти задачи далеко не всегда решаются наилучшим образом. Этим объясняется наличие структур, выведенных из бурения с отрицательным результатом, после того как на них пробурено пять-семь скважин и более. Одновременно большое число перспективных структур длительное время не вводится в бурение из-за недостатка материальных и трудовых ресурсов. Обоснованное решение указанных задач требует учета геологических, технических и экономических факторов, формирования и сравнения множества альтернативных вариантов ведения работ, что трудно сделать, используя только традиционные методы планирования. В этой ситуации эффективно применять экономико-математические методы выбора оптимального решения. Сформулируем условие задачи. Перед началом поисковых работ известны зоны поиска, т. е. структуры, на которых планируется поисковое бурение и, возможно, будут обнаружены объекты поиска - нефтяные месторождения. Общее же число и размеры последних неизвестны. Однако для различных по величине ресурсов С3 структур, вводимых в бурение, на основе имеющейся статистической информации или экспертизы может быть дана оценка возможности обнаружения на них нефтяных месторождений. Как правило, на структурах с незначительными ресурсами С3 скорее будут открыты мелкие месторождения, а с ростом этих ресурсов на перспективных структурах повышается вероятность выявления месторождений со значительными запасами. Сгруппируем структуры в классы по какому-либо признаку, хотя в принципе это можно сделать и по нескольким признакам. Наличие статистических выборок достаточного объема повысит качество вырабатываемых решений, но не повлияет на методику их формирования. Поэтому в дальнейшем будем классифицировать структуры только по величине ресурсов. Для каждого класса на основе статистической обработки информации о величине открытых месторождений можно построить либо непрерывную функцию плотности распределения вероятностей открытия месторождений с различными запасами, либо ее дискретный аналог - гистограмму частоты встречаемости месторождений различных классов. В работе [2] приводятся плотности распределения для структур трех классов (рис. 1).

Введем понятие функции обнаружения нефтяного месторождения для структур различных классов [3]. Пусть  - индекс класса структуры, - величина поискового усилия на данной структуре, под которым можно понимать либо объем поискового бурения, либо число поисковых скважин, либо материальные затраты на поиск, либо какой-нибудь другой показатель. Если на структуре данного класса действительно существует месторождение с запасами z, то функция обнаружения  покажет вероятность выявления этого месторождения. Она должна удовлетворять следующим условиям: а) на структуре может быть открыто месторождение (), если  и , т. е. если оно существует и на структуре ведется поисковое бурение; б) вероятность открытия месторождения равна нулю () при ; в) если на структуре имеется месторождение (z>0), то с ростом объема поисковых усилий вероятность его открытия увеличивается и стремится к единице; г) с ростом z вероятность обнаружения месторождения повышается.

Анализ статистики выявления месторождений показывает, что наибольший процент открытий приходится на первую поисковую скважину, меньший - на вторую, еще меньший - на третью и т. д. Конкретные цифры варьируют по районам, но в любом случае указанные соотношения соблюдаются. На основе данных о распределении структур по числу скважин, затраченных на открытие месторождений, строится функция обнаружения. Если, например, известно, что месторождения определенного класса открывались первой скважиной в 55 % случаев (=0,55), второй - в 25 % (=0,25), третьей - в 10% (=0,1), четвертой - в 5% (=0,05) и т. д., то можно легко построить дискретную функцию обнаружения по следующему правилу: , где k - поисковые усилия, выраженные числом пробуренных скважин. В нашем примере  

Когда поисковые усилия показаны в объемах бурения, можно произвести сглаживание полученной ступенчатой функции . Если по району (направлению работ) отсутствует достаточная статистическая база по уже открытым месторождениям, то функцию обнаружения можно строить и по аналогии с хорошо изученным районом со сходным геологическим строением. Поскольку конкретные значения  зависят от геологической сложности района, то и вид построенной функции обнаружения будет отражать эту сложность. В общем случае чем труднее район, тем меньше значение функции обнаружения для одного и того же усилия поиска. Следует заметить, что в неявном виде функции обнаружения используются при планировании поисковых работ, когда вводится понятие максимального числа поисковых скважин, необходимых для выявления месторождения или заключения о бесперспективности структуры. Так, для оценки структуры в платформенных районах обычно достаточно двух-трех скважин [2], а в районах сложного геологического строения - до семи. В работе [1] функция обнаружения сформулирована практически в явном виде.

Условиям а-г удовлетворяют различные классы вогнутых функций, но чаще всего для аналитической записи непрерывных функций используют модификации экспоненты: . Здесь коэффициент  отражает сложность геологического строения района. На платформе его величина больше, в областях краевых прогибов, районах с многократной тектонической перестройкой и т. п.- меньше (рис. 2). В принципе функции обнаружения можно строить не только для района или направления работ, но и для более мелких геологических объектов. Это позволяет при принятии решений учесть более широкий круг геологических факторов, например приуроченность к зонам развития крупных резервуаров и т. д.

Для формализации задачи в виде экономико-математической модели остается выбрать критерий оптимальности, по которому будут оцениваться результаты той или иной стратегии поиска. При первой постановке задачи (максимальный результат при ограниченных поисковых усилиях) в качестве критерия естественно принять максимум математического ожидания суммарного прироста запасов категории С2 по всем структурам, введенным в поиск.

Предположим, может быть опоисковано n структур. Общий объем поисковых усилий, затраченный на прирост запасов, равен Y. При известных плотностях вероятностей величин открываемых на структурах месторождений  и функциях обнаружения  ожидаемый прирост запасов на одной структуре -го класса можно выразить в виде функции от величины :

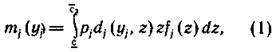
где  - вероятность того, что на -й структуре существует некоторое месторождение. Аналогом этой вероятности выступает коэффициент успешности, рассчитываемый как отношение структур, давших промышленные притоки нефти, к числу опоискованных. Эту вероятность желательно вычислить для каждого класса структур.

С учетом [1] задачу в первой постановке можно формализовать следующим образом. Требуется максимизировать суммарный прирост запасов категории С2 и частично С1 по n структурам, которые могут быть введены в поиск:

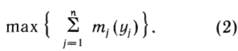
Суммарный объем поисковых усилий не должен превышать мощности организации, ведущей поиск (Y):

Поисковые усилия на каждой структуре положительные:

Методы решения задач (2) - (4) достаточно хорошо известны [3]. Однако они требуют строгой вогнутости и непрерывной дифференцируемости функций обнаружения. Для поиска нефтяных месторождений наиболее объективной единицей измерения величины поискового усилия следует считать законченную бурением и опробованную глубокую скважину, так как только после опробования можно сделать вывод о наличии залежи на структуре. Следовательно, вероятность обнаружения месторождения должна изменяться в зависимости от числа скважин и оставаться постоянной, когда скважина находится в процессе бурения, хотя в это же время растут накопленный объем бурения и затраты на поиск. Поэтому, строго говоря, функция обнаружения должна иметь ступенчатый вид (см. рис. 2, графики 3, 4). Непрерывные функции обнаружения, удовлетворяющие указанным требованиям, могут использоваться в том случае, когда планируются поисковые работы в НГП, крупной НГО и т. д., где осуществляется широкая программа поисков, а объемы бурения и число скважин достаточно велики. Для более мелких геологических объектов необходимо учитывать дискретный характер поискового процесса. В этом случае задачи (2) - (4) могут быть решены методами динамического программирования с помощью рекуррентного соотношения

где - математическое ожидание прироста запасов на первых  структурах при условии, что поисковые усилия равны . Математическое ожидание прироста запасов на отдельной структуре  - дискретный аналог (1) - рассчитывается по формуле

где - номера классов соответственно структуры и месторождения,  - дискретная функция обнаружения, - дискретная плотность вероятности (см. рис. 1, гистограммы).

С помощью выражений (5)-(6) для любого заданного объема поисковых усилий Y можно определить максимальный ожидаемый прирост запасов категории С2, число структур, которые для этого необходимо опоисковать (всего и с разбивкой по классам), очередность ввода их в поиск, количество скважин, которые нужно заложить на каждой из структур.

Поясним на примере. Предположим, что поиск можно вести на четырех структурах трех классов: по одной структуре первого и второго классов и две третьего. Вероятность наличия промышленных залежей нефти на структурах разных классов  равна соответственно 0,6, 0,5, 0,4. При этом могут быть обнаружены месторождения трех классов с запасами 10, 30, 50 млн. т. Следует отметить, что на первых двух структурах может быть выявлено любое из указанных месторождений, а на двух структурах третьего класса только месторождения с запасами 10 и 30 млн. т.

Функции плотности вероятности обнаружения месторождений по классам структур  приведены на рис. 3.

Функции обнаружения, имеющие ступенчатый вид, удобнее представить в виде таблицы.

Так, если на структуре II класса существует месторождение 2-го класса (с запасами 30 млн. т), то вероятность его выявления двумя поисковыми скважинами равна 0,6.

Допустим, организация, ведущая поиск, за некоторый период времени может пробурить девять скважин (y=9). Разместить их по структурам следует так, чтобы прирост запасов M(Y) был максимальным. Решая эту задачу с помощью рекуррентного соотношения (5), получаем, что на первой структуре должно быть пробурено четыре скважины, на второй - три, на третьей и четвертой - по одной, т. е.  Ожидаемый прирост запасов при этом составит 40,7 млн. т. Если Y=6, то   (M (Y) =32,4).

Статистическая постановка задачи, рассмотренная выше, позволяет рациональной распределить поисковые скважины по структурам, но остается нерешенным вопрос об очередности вовлечения их в поиск и о динамике поисковых усилий на каждой из структур. Однако предлагаемая методика позволяет переходить к динамическому ее расширению. Так, если предположить, что рассматриваемый период равен трем годам, а мощность поисковой организации неизменна во времени ( скважинам), то можно определить векторы поисковых усилий по каждой структуре , где  - число поисковых скважин, пробуренных на -й структуре в t-м году. Для этого необходимо последовательно решить три статистические задачи для Y=3, Y=6, Y=9. Параметры решения для -го года получают как разность между решениями для  и  . В нашем примере   , т. е. в первый год на самой крупной структуре бурятся две скважины, на второй по величине - одна, а на двух мелких бурение не ведется. Во второй год на первой структуре закладывается одна скважина, на второй - две, а две последние в бурение не вовлекаются. В третий год прекращаются работы на второй структуре, на первой бурится еще одна скважина и вовлекаются в бурение обе мелкие структуры. Соответственно будут получены следующие приросты запасов: 19,5, 12,9, 8,3 млн. т. Для других векторов мощностей поисковой организации стратегия ведения поискового бурения будет иной, даже если суммарный его объем за период не изменится. Так, при  получим следующее решение задачи:  = 14,6 млн. т, = 13,8 млн. т,  = 12,3 млн. т, т. е. объемы подготовки сдвигаются к концу периода, так как переносится на один год постановка поискового бурения на второй структуре.

Таким образом, предлагаемая методика позволяет определять очередность вовлечения в поисковое бурение отдельных структур, устанавливать оптимальные объемы работ на каждой из них, выбирать такую стратегию работ, которая максимизирует ожидаемые приросты запасов при заданных ограничениях на объемы работ. Кроме того, с ее помощью можно объективно оценить верхнюю границу величины поисковых усилий в районе, превышение которой ни при каких условиях нецелесообразно. Эта граница определяется конкретным видом функции обнаружения. Если  такова, что  для любого , то дополнительные поисковые скважины ни на одной из структур не увеличат ожидаемого прироста запасов. Следовательно, и по району в целом он не изменится. Предельная величина поисковых усилий может определяться так:

В нашем примере Y=15, поскольку при  значения функций обнаружения выходят на верхний предел (см. таблицу).

В заключение отметим, что в качестве критерия может быть выбрано не математическое ожидание прироста, а какая-либо иная статистика, например мода, a-процентная, квантиль или другая. И критерий, и объемы допустимых поисковых работ могут выражаться не в натуральной, а в стоимостной форме. С незначительными изменениями изложенный подход к формированию стратегии поискового бурения позволяет учитывать при разработке планов требования к надежности подготовки запасов. И наконец, если число введенных в поиск структур достаточно велико, то по результатам расчетов можно определить не только общую величину ожидаемого прироста запасов, но и их структуру, т. е. количество месторождений с запасами разной величины.

СПИСОК ЛИТЕРАТУРЫ

1.      Габриэлянц Г.А., Пороскун В.И., Сорокин Ю.В. Методика поисков и разведки залежей нефти и газа. М., Недра, 1985.

2.      Основы формирования комплексной программы повышения эффективности и оптимального размещения поисково-разведочных работ на нефть / М.М. Саттаров, Э.М. Ясин, В.П. Ильченко и др. М., ВНИИОЭНГ, 1980.

3.      Хеллман О. Введение в теорию оптимального поиска. М., Наука, 1985.

 

Таблица

Класс

Поисковое усилие (число скважин)

структуры

месторождения

y=1

y=2

y=3

y=4

y=5

вероятности (значения  для различных )

I

1

0,2

0,5

0,7

0,9

1,0

2

0,3

0,6

0,8

0,9

1,0

3

0,4

0,7

0,9

1,0

1,0

II

1

0,2

0,5

0,8

1,0

1,0

2

0,3

0,6

0,9

1,0

1,0

3

0,4

0,7

0,9

1,0

1,0

III

1

0,5

0,8

1,0

1,0

1,0

2

0,5

0,9

1,0

1,0

1,0

 

Рис. 1. Гистограммы и плотности вероятностей распределения месторождений по величине запасов на структурах с балансовыми ресурсами С3 (млн. т): 0,8-1.6 (а), 1,6-3,2 (б), 3,2-6,4 (в)

 

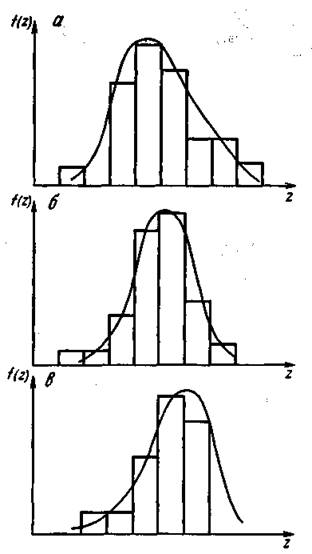
Рис. 2. Функции обнаружения непрерывного и дискретного вида для одинаковых по запасам месторождений на структурах одного класса в районах простого (1,3) и сложного (2,4) геологического строения

 

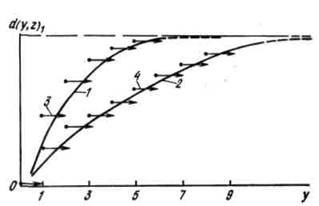
Рис. 3. Вероятности обнаружения месторождений с запасами 10, 30, 50 млн. т на структурах I-III классов