|
УДК 550.822.3 |
Определение коэффициента сжимаемости пустотного пространства коллектора по данным исследований на неустановившихся режимах фильтрации
В.А. КОРОТЕНКО, М.Е. СТАСЮК (ЗапСибНИГНИ)
При определении коэффициента сжимаемости пустотного пространства коллекторов баженовского типа g в лаборатории возникают трудности, вызванные разрушением породы при отборе керна и высверливании образцов. Поэтому представляет интерес и является актуальной разработка методик оценки его по данным гидродинамических исследований.
Методы определения
g по данным исследований на установившихся режимах фильтрации
были предложены ранее [2, 3, 5, 6]. Однако до настоящего времени им не
уделялось должного внимания. В работе [3] для определения влияния деформаций на
фильтрационные свойства коллектора предлагается использовать кривые падения
давления (КПД). При этом допускается, что характер изменения его проницаемости
при снижении давления описывается экспоненциальной зависимостью и обусловлен
процессами деформации пустотного пространства. Методика [7], основанная на
обработке КПД интегральным методом Умрихина - Чарного (упрощение Б.А. Богачева),
позволяет определить начальную гидропроводность и коэффициент 
, характеризующий зависимость гидропроводности
пласта от параметра 
.
На основании этой методики был разработан способ определения g [4], однако его
применение связано с графическими построениями, что вызывает некоторые
затруднения. Во-первых, достоверность результатов зависит не только от
экспериментальных данных, но и от точности обработки и аппроксимации кривой;
во-вторых, определение искомых параметров возможно только в том случае, когда
КПД имеют достаточно четкую криволинейную форму.
Нами предлагается усовершенствованная методика определения g и зависимости проницаемости от депрессии по данным исследований на неустановившихся режимах фильтрации. Получены формулы, позволяющие находить искомые параметры без графического построения, что существенно снижает трудоемкость процесса вычисления, усовершенствован графический метод обработки [4]. Рекомендуемая методика позволяет установить зависимость g от давления и вести обработку исходных данных как с учетом, так и без учета притока жидкости в ствол скважины после ее остановки.
Для оценки этих
зависимостей воспользуемся следующими предположениями. Допустим, коэффициент,
характеризующий зависимость проницаемости от давления, есть функция депрессии 
. Тогда текущее значение
проницаемости определяется по формуле
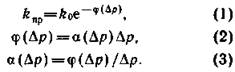
Если 
, получим общеизвестные
формулы [5].
Коэффициент гидропроводности e зависит линейно от Кпр. Считая эффективную мощность и вязкость постоянными, можно записать
где 
- гидропроводность начальная и
текущая.
В работе [3] приводится зависимость гидропроводности от депрессии для КПД:
где 
- импульс депрессии,
- приток жидкости в ствол
скважины, 
-
коэффициент зависимости гидропроводности от 
.
Ниже предлагаются
способы определения коэффициента 
для различных методов обработки КПД. Известно, что
гидропроводность обратно пропорциональна тангенсу угла наклона 
преобразованной КПД.
Для двух различных
значений 
и 
после логарифмирования
можно записать
Из (3)
где 
- среднее значение в интервале,
откуда
Из формулы (6)
следует, что если КПД аппроксимируется прямой линией, то коэффициенты 
и 
постоянны. Другой способ
определения основывается на методике [4, 7]. Из (4) и (5) следует:
Из (3)
Для пользования
формулой (7) нужно знать 
. Для этого необходимо построить КПД в координатах 
, найти значение 
в различных точках,
построить зависимость 
от
и по соотношению
(8) рассчитать 
:
Значения 
можно вычислить,
пользуясь аналитическим методом определения 
без учета притока. Согласно [1]
где 
Из (6) и (9) имеем
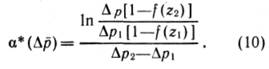
В случае притока жидкости к стволу скважины из (8) получим
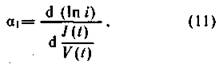
Из приближенной формулы интегрального метода Умрихина - Чарного можно записать
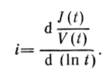
После преобразования (11) получим
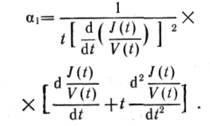
Пренебрегая
членами, содержащими 
и
учитывая (7):
Если вторым слагаемым в (12) пренебречь, то
Коэффициент
сжимаемости пустотного пространства 
по известному значению 
или 
найдем по формуле [6]
где 
- коэффициент сжимаемости нефти,
2*10-3 МПа-1
В качестве примера
определения 
рассмотрим
данные обработки КПД по скв. 25, 42, 125 Салымского месторождения. В первых
двух они обрабатывались с учетом притока жидкости в ствол скважины после ее
остановки, а в скв. 125 - без учета притока.
Обработка КПД по
скв. 25 графоаналитическим методом с использованием формулы (8) затрудняется
из-за большого радиуса кривизны КПД, поэтому
определялся по формулам (12) и (14).
Запись КПД
продолжалась 8,5 ч, депрессия возросла от нуля до 19,5 МПа. Если не
рассматривать начальный участок КПД ввиду наибольшей неточности
экспериментальных данных, то коэффициент 
меняется в пределах 0,0455-0,0537 МПа-1, 
- в интервале
0,0145-0,0172 МПа-1. При определении графоаналитическим методом
указанных коэффициентов для скв. 42 по формулам (8), (14) использовали
результаты обработки, приведенные в [7]. Значения этих коэффициентов находили
также по формулам (8), (12) - (14):
Значения,
полученные графоаналитическим методом по (8), (14), отличаются от полученных
аналитически по (12), (14) в среднем на 16 %; результаты более грубого
приближения по (13), (14) - в среднем на 8 %. При этом следует учитывать, что
графоаналитическая обработка связана с точностью графических построений, что
также увеличивает вероятность ошибки при определении 
. При обработке результатов исследования
скв. 125 без учета притока в ствол скважины 
рассчитывали по формулам (6), (10), (12), (14). Если
начальный участок КПД не учитывать, то наиболее удовлетворительные результаты
дает применение формулы (12):
Выводы
1. Разработан аналитический метод определения g по данным исследования скважин на неустановившихся режимах фильтрации.
2. В отличие от ранее предложенного [4,7], данный метод учитывает изменение сжимаемости в зависимости от депрессии на пласт и характеризуется более высокой точностью и разрешающей способностью.
СПИСОК ЛИТЕРАТУРЫ
1. Бузинов С.П., Умрихин И.Д. Гидродинамические методы исследования скважин и пластов. М., Недра, 1973.
2. Горбунов А.Т. Разработка аномальных нефтяных месторождений. М., Недра, 1981.
3. Горбунов А.Т., Николаевский В.Н. О нелинейной теории упругого режима фильтрации.- НТС, Сер. Добыча нефти, М., Недра, 1964, с. 73-95.
4. Горностаев С.Г., Нестеров В.Н., Пешков В.Е. Метод определения упругости продуктивных отложений баженовской свиты по результатам гидродинамических исследований (Тез. докл. 6-й научно-технической конференции молодых ученых и специалистов). Тюмень, ЗапСибНИГНИ, 1983, с. 85-86.
5. Котяхов Ф.И. Физика нефтяных и газовых коллекторов. М., Недра, 1972.
6. Медведский Р.И., Стасюк M.Е. Метод обработки результатов исследования на неустановившихся режимах фильтрации.- В кн.: Комплексирование геолого-геофизических исследований в скважинах. Тюмень, 1983, с. 25-30.
7. Пешков В.Е., Нестеров В.Н., Асаева Е.Е. Геолого-экономическая эффективность применения рациональной технологии испытания скважин Салымского месторождения.- В кн.: Пути повышения эффективности бурения и испытания разведочных скважин. Тюмень, 1975, с. 87-92.