|
УДК 550.834 |
Сейсмическая миграция с учетом преломления лучей на промежуточных границах
В.В. ПОПОВ (ВНИИгеофизика)
В настоящее время наиболее широко используются методы построения динамических глубинных разрезов, применение которых ограничено углами наклона и кривизной границ, а также основанные на модели среды средних скоростей. В районах со сложным строением среды это приводит к неполному учету преломления сейсмических лучей на промежуточных криволинейных сильнопреломляющих границах и, как следствие, к погрешности миграционных построений.
В данной статье рассматривается метод послойной миграции, обеспечивающий преобразование временных разрезов МОГТ в динамические глубинные разрезы с учетом преломления лучей на промежуточных границах. Решение задачи основано на применении модифицированного интеграла Кирхгофа, причем особое внимание уделяется преломлению на небольшом числе сейсмических границ. В промежутках между ними предполагается, что справедлива модель среды, описываемой средними скоростями. Это, с одной стороны, позволяет существенно упростить обработку данных, так как преломление учитывается лишь на нескольких границах, а с другой - дает возможность учесть геометрию сильно преломляющих границ. Вероятно, этот подход является обоснованным, потому что реальная геологическая среда в промежутках между преломляющими границами, как правило, хорошо аппроксимируется моделью средних скоростей в условиях солянокупольной тектоники.
Модифицированный
интеграл Кирхгофа для плоских границ наблюдения при решении двумерных задач
(наблюдения проведены вдоль некоторого профиля![]() ) в рамках метода спуска можно представить в виде
) в рамках метода спуска можно представить в виде
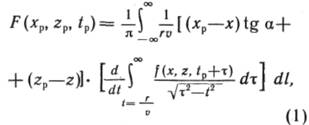
где ![]() - момент времени, в который
рассчитывается волновое поле F в точке среды
- момент времени, в который
рассчитывается волновое поле F в точке среды ![]()
![]() расстояние от этой точки до точек
расстояние от этой точки до точек ![]()
![]() линии
линии ![]() , на которой зафиксировано наблюденное поле
, на которой зафиксировано наблюденное поле ![]() ,
,![]() - половинная скорость,
- половинная скорость,![]() - угол наклона линии наблюдения в
точках
- угол наклона линии наблюдения в
точках![]() ,
,![]() ,
,![]() - переменная интегрирования.
- переменная интегрирования.
Используя
выражение (1), можно построить волновое поле в однородно-слоистой среде путем последовательного
его восстановления в каждом слое (Васильев С.А., Голосов В.П., Полшков М.К., Урупов А.К.
Принципы цифровой
обработки и интерпретации сейсмозаписей отраженных волн на основе
математического описания восстановления волновых полей // Прикладная геофизика,
вып. 66. М.: Недра.- 1972.- С. 8-24.). Пусть линия ![]() - кровля
- кровля ![]() го слоя, скорость распространения волн в
этом слое
го слоя, скорость распространения волн в
этом слое ![]() . Кровля
первого слоя
. Кровля
первого слоя ![]() является
линией наблюдения. Тогда по соотношению (1) можно продолжить поле в первый слой
до его подошвы - границы
является
линией наблюдения. Тогда по соотношению (1) можно продолжить поле в первый слой
до его подошвы - границы ![]() и определить ее положение. Зная положение границы
и определить ее положение. Зная положение границы ![]() , с помощью выражения
(1), рассчитываем поле на
, с помощью выражения
(1), рассчитываем поле на ![]() , т. е. приводим наблюдения к этой границе. Далее,
восстанавливаем волновое поле под
, т. е. приводим наблюдения к этой границе. Далее,
восстанавливаем волновое поле под ![]() вплоть до границы
вплоть до границы ![]() и т. д.
и т. д.
Такой подход к построению динамических глубинных разрезов позволяет перейти от аппроксимации реальной геологической среды моделью средних скоростей к более точному ее описанию моделью среднепластовых скоростей и учесть кривизну сейсмических границ.
Для правильного
восстановления не только кинематических, но и динамических характеристик
волнового поля F (в
рамках волнового уравнения), знание величины поля на линии наблюдения ![]() недостаточно. Известно,
что интеграл (1) дает решение волнового уравнения, воспроизводящее граничные
условия. Например, если продолжать поле плоской волны по интегралу (1) внутрь
горизонтально-слоистой среды, то на каждой границе волна будет иметь ту же
амплитуду, что и на линии наблюдения. Это не соответствует реальной ситуации,
поскольку волна, идущая вверх, постепенно расходует свою энергию на обратные,
направленные вниз, отражения, и ее амплитуда изменяется.
недостаточно. Известно,
что интеграл (1) дает решение волнового уравнения, воспроизводящее граничные
условия. Например, если продолжать поле плоской волны по интегралу (1) внутрь
горизонтально-слоистой среды, то на каждой границе волна будет иметь ту же
амплитуду, что и на линии наблюдения. Это не соответствует реальной ситуации,
поскольку волна, идущая вверх, постепенно расходует свою энергию на обратные,
направленные вниз, отражения, и ее амплитуда изменяется.
Для динамически правильного продолжения поля необходимо обеспечить подкачку энергии обратноотраженных волн в восходящую волну при ее продолжении через преломляющую границу. Для этой цели используется модифицированный интеграл Кирхгофа в сочетании с соответствующими граничными условиями.
Модифицированный интеграл Кирхгофа, содержащий член с производной поля по нормали n к поверхности наблюдения, можно записать в виде
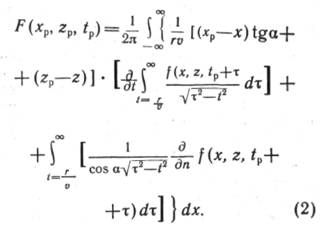
Если под F понимать поле давлений, то при послойном его продолжении граничные условия имеют вид
![]()
где ![]() и
и ![]() - поле и его производная на
- поле и его производная на ![]() в верхнем слое,
в верхнем слое,![]() и
и ![]() - те же параметры на
- те же параметры на ![]() в нижнем слое;
в нижнем слое;![]() и
и ![]() - плотность среды сверху и снизу
от
- плотность среды сверху и снизу
от ![]() . Ниже приведены
результаты применения описанных алгоритмов при обработке полевых данных. На рисунке (а) показан исходный временной разрез МОГТ по профилю,
расположенному в районе развития солянокупольной тектоники на площади Манаш
Прикаспийской впадины. Изменение мощности соли обусловливает временную аномалию
. Ниже приведены
результаты применения описанных алгоритмов при обработке полевых данных. На рисунке (а) показан исходный временной разрез МОГТ по профилю,
расположенному в районе развития солянокупольной тектоники на площади Манаш
Прикаспийской впадины. Изменение мощности соли обусловливает временную аномалию
![]() на подсолевых
границах до 300 мкс. При миграции по модели средних скоростей, несмотря на учет
горизонтального градиента скорости (задавалось 13 скоростных законов), рельеф
кровли соли оказывает влияние на положение подсолевых границ. На рисунке
(б, в) приведены варианты послойной миграции по интегралу (1), которые
иллюстрируют ее эффективность и показывают зависимость получаемых результатов
от правильности задания модели среды. Результат, представленный на рисунке (б), получен по соотношению (1) с учетом преломления
на двух границах А и Б (см. рисунок, a).
на подсолевых
границах до 300 мкс. При миграции по модели средних скоростей, несмотря на учет
горизонтального градиента скорости (задавалось 13 скоростных законов), рельеф
кровли соли оказывает влияние на положение подсолевых границ. На рисунке
(б, в) приведены варианты послойной миграции по интегралу (1), которые
иллюстрируют ее эффективность и показывают зависимость получаемых результатов
от правильности задания модели среды. Результат, представленный на рисунке (б), получен по соотношению (1) с учетом преломления
на двух границах А и Б (см. рисунок, a).
Подсолевые горизонты погружаются моноклинально, причем угол наклона выдерживается по профилю, благодаря чему горизонты четко идентифицируются через разрыв. Для сравнения на рисунке (в) приведена обработка с учетом преломления сейсмических лучей только на одной (наиболее сильной) границе Б. При сопоставлении мигрированных разрезов на рисунке (б и в) наблюдается различное положение подсолевых границ, поэтому миграцию с учетом преломления рекомендуется применять в итерационном режиме с последовательным уточнением модели среды.
Разрез, полученный по соотношению (2), в структурном отношении идентичен разрезу на рисунке (б), но характеризуется более высоким соотношением сигнал/помеха, благодаря чему удается проследить подсолевые горизонты в зоне нарушения корреляции.
Приведенные экспериментальные данные подтверждают эффективность разработанных алгоритмов послойной миграции на основе использования интеграла Кирхгофа при незначительном возрастании затрат времени счета на ЭВМ.
Рисунок Результат применения послойной миграции на площади Манаш:
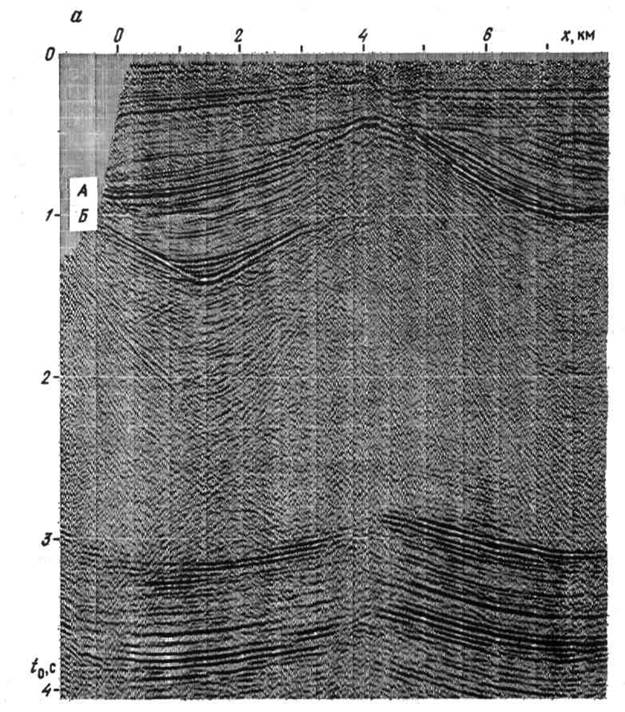
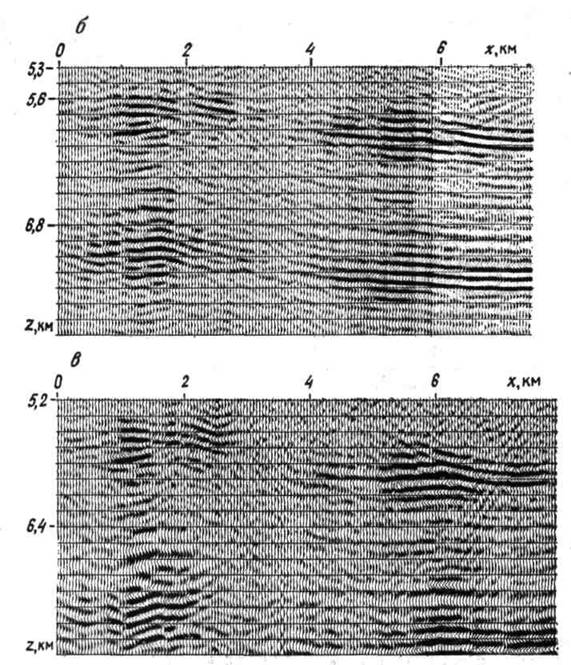
а - исходный временной разрез МОГТ; б - изображение среды, полученное по соотношению (1) с учетом преломления лучей на двух границах; в - то же на одной границе