К оглавлению

УДК 55/51

Имитационное математическое моделирование стохастических процессов как инструмент количественной оценки перспектив нефтегазоносности

А.Э. КОНТОРОВИЧ (НПО «Сибгео»), В.Р. ЛИВШИЦ (Новосибирский гос. ун-т)

Долгосрочное прогнозирование состояния сырьевой базы нефтяной и газовой промышленности является исходным элементом при формировании программы развития топливно-энергетического комплекса. Актуальность и экономическая значимость решения этой проблемы, глобальный характер ее резко повысили в последние десятилетия внимание к количественной оценке перспектив нефтегазоносности отдельных регионов, мегарегионов, стратисферы в целом, к теоретическому и методологическому основанию такого прогноза. Одновременно резко возросли требования к точности прогноза, расширился круг задач, решение которых совершенно необходимо. При этом математические методы стали надежным инструментом геолога. В качестве аппарата при решении прогнозных задач геологии нефти и газа чаще всего используется теория вероятностей и математическая статистика, в частности корреляционно-регрессионный анализ и теория распознавания образов [2, 3, 5]. Широкий круг задач, в частности прогноз с точностью до залежи, месторождения распределения скоплений нефти и газа по запасам в нефтегазоносном бассейне (НГБ), иными словами в генеральной совокупности (статические задачи прогноза), и прогноз динамики выявляемости отдельных месторождений, т. е. динамики формирования выборочных совокупностей (динамические задачи прогноза), может быть решен методом имитационного математического моделирования стохастических процессов - методом Монте-Карло (Н.П. Бусленко, Ю.А. Шрейдер, 1961 г., И.М. Соболь, 1973 г.). На целесообразность использования этого математического аппарата обращалось внимание и раньше [4], однако методика решения конкретных задач и примеры их применения к моделям реальных или теоретически мыслимых объектов отсутствовали. Проводимые в настоящее время в СНИИГГиМСе и Новосибирском гос. ун-те исследования имеют своей целью восполнить этот пробел, опираясь на терминологию и классификацию [2].

Для решения статических задач прогноза распределения месторождений нефти и газа по крупности используется аналитическая модель [1], согласно которой размещение месторождений УВ по величине запасов для любого НГБ подчиняется усеченному закону Парето. Для некоторого НГБ А с заданными начальными геологическими ресурсами (НГР) Q, по методике, описанной ранее [1], определяются необходимые параметры. Затем на ЭВМ генерируется последовательность случайных чисел, статистические характеристики которых отвечают усеченному закону Парето. Каждое такое число получается как решение уравнения, левая часть которого представляет собой интегральную функцию усеченного распределения Парето, а правая - реализацию числа, имеющего равномерное на интервале (0,1) распределение. Если параметры усеченного закона Парето обозначить через , то уравнение для получения числа с таким распределением будет иметь вид

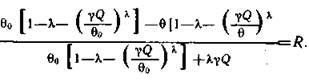
Последовательность случайных чисел  генерируется до тех пор, пока не будет достигнуто заданное значение Q. При этом каждое число имитирует запасы некоторого месторождения в НГБ А. Поскольку формирование залежей УВ естественно рассматривать как процесс (нафтидогенез), имеющий стохастическую природу, то полученная последовательность не является единственно возможной реализацией совокупности месторождений НГБ А. Метод статистических испытаний дает достаточно большое число таких реализаций. Полученные совокупности месторождений могут быть упорядочены по величине запасов, например, от самого крупного к самому мелкому, после чего может быть выполнена статистическая обработка информации о запасах месторождения с фиксированным по величине запасов номером.

В качестве примера рассмотрим НГБ А с Q=1000 условных единиц (УЕ) и параметрами усеченного распределения Парето . Для такого НГБ было получено 100 реализаций совокупности залежей УВ. Некоторые из них показаны на рис. 1. Здесь по оси абсцисс отложены величины запасов месторождений, а по оси ординат - отдельные реализации. На рис. 1, а принята линейная, а на рис. 1, б - логарифмическая шкала значений запасов месторождений. Наглядно видно, что запасы мелких месторождений в различных реализациях образуют практически единые сплошные ряды значений, а расслоение, стратификация месторождений по запасам имеет место лишь при достаточно больших Q. Статистическая обработка полученных реализаций показала, что наиболее варьируют запасы самого крупного в НГБ месторождения - от 36,36 до 540,39 УЕ, среднее - 152,57 УЕ, коэффициент вариации - 62,3 %. С уменьшением запасов месторождения диапазон его возможных значений и коэффициент вариации достаточно быстро убывают. Так, запасы десятого месторождения в НГБ А в 10 раз меньше самого крупного, а коэффициент вариации равен 21,9 %, двадцатого соответственно составляют в среднем 8,4 УЕ и 16,8%, пятидесятого - 3,2 УЕ и 16,8%, сотого - 2 УЕ и 15,4%. Важно отметить, что уже с пятнадцатого месторождения нарушается монотонное уменьшение коэффициента вариации, и от 15 до 120 он изменяется от 17,2 до 15,4 %.

Таким образом, как показали вычислительные эксперименты на ЭВМ, разнообразие и индивидуальность отдельных реализаций проявляются главным образом в большом разбросе возможных запасов залежей первых пяти-шести, максимум десяти наибольших по запасам месторождений и, в первую очередь, в массе УВ в самом крупном из них - гиганте. Что касается размеров основной массы месторождений, то их запасы контролируются параметрами бассейна с достаточно высокой степенью точности.

Отсюда, в частности, следует, что при количественной оценке перспектив нефтегазоносности слабоизученных бассейнов, когда наиболее крупные месторождения еще не выявлены, при прогнозе структуры НГР точно предсказать их размеры крайне трудно, по существу, со сколько-нибудь значительной точностью невозможно. В подобной ситуации целесообразно брать средние величины по большому числу реализаций и задавать с определенной доверительной вероятностью возможный интервал значений.

По нашему мнению, представляет интерес обсудить проблему интерпретации полученных результатов с гносеологической точки зрения. Как следует рассматривать возможную вариацию запасов, начиная с самого крупного по величине запасов месторождения в НГБ А в описанном эксперименте? Отражает ли это вероятностную природу моделируемого процесса или является лишь следствием выбранного метода решения? Хотя процесс нефтегазообразования в любом НГБ протекает по единым общим законам, конкретное развитие НГБ помимо этого контролируется большим количеством незакономерно флюктуирующих случайных факторов, и получение в численном эксперименте конкретной реализации или совокупности реализаций представляет собой моделирование реально существующей стохастичности процесса нафтидогенеза. В этом смысле в соответствии с идеями А.Н. Колмогорова вероятность Р появления при заданных условиях S (объем осадочного выполнения бассейна, его геометрия, начальные геологические ресурсы УВ и т. п.) самого крупного в бассейне месторождения с запасами  и т. п. следует рассматривать как отражение объективного характера стохастической связи между историей НГБ и закономерностями нафтидогенеза в нем, а саму вероятность Р как меру определенности появления самого крупного месторождения именно с такими запасами.

Рассмотрим теперь применение метода статистического моделирования для решения динамических задач прогноза распределения месторождений нефти и газа по крупности. Исходным моментом является генеральная совокупность месторождений НГБ А. Процесс имитации геологоразведочных работ преобразует эту совокупность в выборочную, месторождения в которой упорядочены в порядке их выявления. Указанное преобразование заключается в последовательном извлечении элементов генеральной совокупности в соответствии с некоторым вероятностным распределением. Последнее таково, что вероятность попадания элемента генеральной совокупности в выборочную неодинакова для различных месторождений и зависит, прежде всего, от величины запасов месторождения. Процесс имитации заключается в расчете распределения вероятностей и извлечении элементов генеральной совокупности в соответствии с ним.

Будем рассматривать НГБ А, содержащий N месторождений  как некоторую гипотетическую генеральную совокупность, а процесс выявления их как последовательный случайный выбор без возвращения элементов генеральной совокупности. Пусть к какому-то моменту  было открыто  месторождений, которые составляют выборочную совокупность. Выпишем их в порядке открытия , где - некоторая перестановка из чисел 1, ... К,  - месторождение генеральной совокупности  открытое -м по порядку в  -ой реализации выборочной совокупности. Последовательность выявленных месторождений представляет собой реализацию (К-1) связной цепи Маркова, вероятностное распределение которой задается как

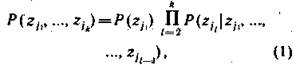
где - условная вероятность того, что в реализации процесса выбора элемент  был выбран -м при условии, что перед ним элементы выбирались в порядке. Определение вероятности  ни из содержательных соображений, ни из эмпирических данных не представляется возможным, по крайней мере, на данном этапе исследований.

Возможный путь решения задачи заключается в том, чтобы, сформулировав разумные требования, основанные на общих соображениях о геологоразведочном процессе и имеющихся эмпирических данных, попытаться найти не саму вероятность , а некий аналог, достаточно точно описывающий реальный геологоразведочный процесс. Точность его и может служить критерием правильности построенной модели.

Исследование закономерностей в реальном геологоразведочном процессе позволяет выбрать в качестве вероятности  функцию  вида

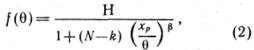
где - величина запасов месторождения,  - некоторые параметры, Н - нормирующий множитель.

В соответствии с понятием «геологоразведочный фильтр» (В.И. Шпильман, 1982 г.) функцию  в дальнейшем будем называть функцией фильтрации, а параметр  - показателем качества фильтра. По данным Н.П. Бусленко и Ю.А. Шрейдера (1961 г.) при =0 вероятность попадания в выборочную совокупность не зависит от  и одинакова для всех месторождений остаточной совокупности. Это случай отсутствия фильтра. При  фильтр становится идеальным, т.е. месторождения попадают в выборочную совокупность строго по порядку от самого большого к самому малому. Для получения конкретных реализаций выборочной совокупности воспользуемся методом статистического моделирования. Сначала, как было рассмотрено выше, сформируем генеральную совокупность месторождений. Затем будем производить последовательный случайный выбор элементов этой совокупности, причем каждый элемент выбирается с вероятностью, определяемой по Н.П. Бусленко и Ю.А. Шрейдеру (1961 г.).

Проиллюстрируем изложенное на конкретном примере. Сразу же заметим некоторые особенности и «преимущества» такого подхода по сравнению с природным процессом. В реальной ситуации начальные геологические ресурсы нефти и газа, равно как и запасы открытых месторождений оцениваются с некоторой, в зависимости от задачи и объекта, погрешностью, что, как следствие, вносит погрешность в определение коэффициента разведанности начальных геологических ресурсов и параметров генеральной совокупности и усложняет, искажает наблюдаемые закономерности. В проведенных численных экспериментах эти погрешности не моделировались и процесс исследован, так сказать, в неискаженном виде.

Второе преимущество выполненных экспериментов - возможность моделировать процесс до его логического конца, т. е. открытия всех месторождений в НГБ. В реальном геологоразведочном процессе такая полная исчерпаемость открытий, естественно, невозможна. Более того, в хорошо изученных НГБ коэффициент разведанности начальных геологических ресурсов УВ вряд ли превышает в настоящее время 0,7-0,8. Поэтому характер процесса при более высоких значениях этого показателя в пределе мы можем только предполагать.

Наконец, в реальной ситуации каждый НГБ может быть изучен только один раз и поэтому не всегда можно отличить какие из особенностей этого процесса носили закономерный, а какие случайный характер. В вычислительном эксперименте имитация процесса поисков месторождений в НГБ теоретически может быть повторена неограниченное количество раз при одном и том же значении показателя качества фильтра (разные реализации) или разных его величинах, что позволяет решить и этот вопрос

В качестве генеральной совокупности вы берем из полученных выше реализаций с номером 1. На рис. 2 показаны последовательности открытия разных по запасам месторождений в отдельных реализациях при значениях показателя качества фильтра , равных 0, 0,85 и 7. При отсутствии фильтра (=0) открытие любого по запасам месторождения равновероятно. Как следствие, наиболее крупное по запасам месторождение может быть обнаружено на ранних (реализация III), средних (II) и поздних (I) стадиях изучения НГБ. Иное отмечается при среднем качестве фильтра (=0,85) - хорошо видно, что наиболее крупные по запасам месторождения открываются в числе первых 15-30, а начиная примерно с сотого флюктуации в запасах выявляемых месторождений очень незначительны. Эта закономерность проявляется еще более отчетливо при =7 (см. рис. 2, в). В случае отсутствия фильтра каждое месторождение в НГБ может быть открыто при любом из возможных значений показателя разведанности НГР. С повышением качества фильтра среднее значение коэффициента разведанности, при котором открывается месторождение, увеличивается с уменьшением запасов месторождения, одновременно убывает диапазон возможных значений этого показателя.

Сравнение различных статистических характеристик выборочных реализаций с соответствующими реального геологоразведочного процесса позволяет сделать вывод о перспективности применения метода статистических испытаний при решении задач нефтяной геологии.

СПИСОК ЛИТЕРАТУРЫ

1. Конторович А.Э., Демин В.И. Прогноз количества и распределения по запасам месторождений нефти и газа.- Геология и геофизика, 1979.- № 3.- С. 26-46.

2. Конторович А.Э., Демин В.И., Страхов И.А. Закономерности выявления различных по запасам месторождений нефти и газа в нефтегазоносных бассейнах.- Геология и геофизика.-1985.-№ П.-С. 3-15.

3. Методы оценки перспектив нефтегазоносности /Под ред. Н.И. Буялова и В.Д. Наливкина.- М.: Недра.- 1979.

4. Метод Монте-Карло в нефтяной геологии /М.Д. Белонин, Ю.В. Подольский, И.С. Симакова, В.А. Шейман // Обзор. Сер. матем. методы исслед. в геологии.- М.: ВИЭМС.- 1981.

5. Прогноз месторождений нефти и газа /А.Э. Конторович, Э.Э. Фотиади, В.И. Демин и др.-М.: Недра. 1981.

Рис. 1. Стратиграммы некоторых реализаций генеральной совокупности месторождений в линейном (а) и логарифмическом (б) масштабах

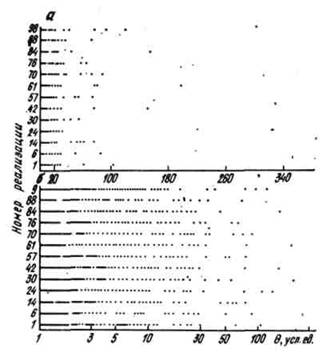
Рис. 2. Последовательность открытия различных по запасам месторождений в НГБ А при =0 (а),  =0,85 (б),=7 (в):

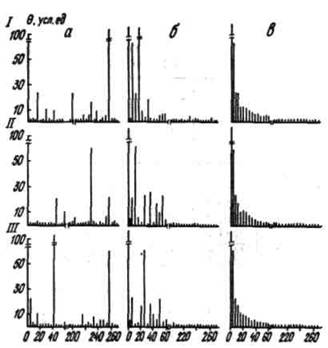
I-III - разные реализации