|
УДК 553.98:553.046 |
Экономико-математическая модель прогнозирования прироста запасов нефти и добычи
М.Т. АБАСОВ, А.М. КУЛИЕВ, А.А. АЛИЕВ, В.М. ВАЛИЕВ (ИПГНМ)
Основным источником устойчивого развития добычи нефти и газа на длительную перспективу в любом нефтегазодобывающем регионе является ввод новых мощностей, создание которых требует подготовки и вовлечения в активную разработку необходимых объемов новых извлекаемых запасов. Объемы прироста запасов и добычи ископаемых зависят от выделяемых капитальных вложений на поисково-разведочные работы, разработку месторождений, а также от степени их эффективности за счет ускорения внедрения результатов научно-технического прогресса. В этих изменяющихся во времени условиях важное значение имеет прогнозирование динамики оптимальных объемов прироста запасов и добычи нефти и газа. Вопросам планирования прироста запасов и добычи посвящены исследования А.П. Крылова, А.А. Трофимука, М.М. Саттарова, Ю.П. Борисова, А.И. Гриценко, Л.П. Гужновского, Ю.П. Желтова, М.Д. Розенберга и др. Например, в работах [1, 3, 6] оптимальное соотношение между приростом запасов и добычей нефти определяется по минимуму суммарных капитальных затрат на разведку и разработку с использованием различных технологических показателей в качестве управляющих параметров. Управляющим параметром [1] служит максимальный темп отбора, оптимальное значение которого определяется в предположении, что все новые запасы в рассматриваемом плановом периоде вводятся в разработку по единому закону изменения темпа отбора, тогда как в [3, 6] использованы запасы, приходящиеся на одну скважину, и кратность запасов нефти, для чего выбираются оптимальные значения на каждом промежутке (год или пятилетка) периода планирования.
Ниже рассматривается экономико-математическая модель, для которой сформулирована и решена с помощью метода динамического программирования задача определения оптимального соотношения между приростом запасов нефти и добычей из них, по критерию минимума суммарных дисконтированных капитальных вложений в разведку и разработку, отнесенных к единице добываемой в плановый период продукции, где в качестве управляющих параметров приняты максимальные темпы отбора. Эта модель позволяет учитывать структурные особенности развития нефтегазодобычи и возможные изменения коэффициентов удельных капитальных затрат вследствие влияния горно-геологических условий и научно-технического прогресса.
Приведем математическое описание данной модели.
Пусть по региону задан
уровень добычи нефти 
на
весь плановый период 
.
Предположим, что до начала периода планирования в регионе введены в разработку
извлекаемые запасы в объеме V0.
В общем случае эти запасы качественно неоднородны и состоят из совокупности
извлекаемых запасов 
,
n= 1,2, ... N, введенных в
разработку в различных предплановых промежутках времени. Так как добыча нефти
из этих запасов осуществляется с различными темпами, то модели и методы
прогнозирования, а, следовательно, определенные с их помощью прогнозные уровни
добычи -
в общем
случае будут отличаться друг от друга.
Так, считая 
и 
величинами известными, можно определить уровень
дефицита добычи нефти 
без
учета новых мощностей:
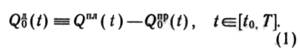
Отметим, что 
могут принадлежать к
различным классам функций. В предлагаемой экономико-математической модели эти,
а также другие, показатели определяются для каждого промежутка периода
планирования и рассматриваются как дискретные, а именно:
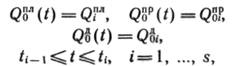
где 
- промежутки равной (можно и
неравной) длины, в частности, годы или пятилетки, на которые разбивается весь плановый
период
; s – число промежутков.
Допустим, что до
какого-то промежутка этого периода плановый уровень добычи нефти по региону
обеспечивается за счет извлекаемых запасов V0.
Обозначим через 
промежуток
планирования, в котором в первый раз образовывается дефицит уровня добычи 
по всему региону, что в
соответствии с (1) определяется:
Причем, 
для 
и 
.
Для восполнения этого
дефицита уровня добычи с начала 
-го промежутка планирования, т. е. с момента времени 
, необходимо ввести в
разработку новые извлекаемые запасы, объем которых 
вычисляется по формуле:
Здесь и далее 
- темп отбора нефти в
момент времени t из извлекаемых запасов 
, вводимых с начала 
го промежутка
планирования: 
.
Темп отбора 
является
хорошо известной нормированной функцией, т. е.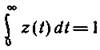 
, поскольку 
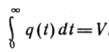. Она принадлежит к некоторому
однопараметрическому семейству функций, где параметром служит максимальный темп
отбора 
. Здесь 
- момент времени, в
котором темп добычи 
достигает
своего максимального значения.
Прогнозные значения уровня добычи нефти из запасов вычисляются по формуле:
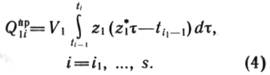
Очевидно, что 
. Находятся
скорректированные значения дефицита уровня добычи нефти:
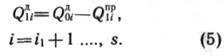
Допустим, что 
для
, а 
. Тогда, для восполнения дефицита уровня
добычи, образовавшегося в 
-ом промежутке планирования, с момента времени 
необходимо вводить в
разработку дополнительные извлекаемые запасы нефти в объеме V2:
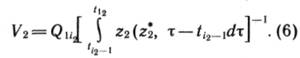
Вычисляются прогнозные значения уровня добычи нефти из запасов V2:
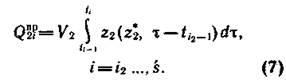
Очевидно, что 
.
Используя полученные из (5) и (7) значения, вычисляются скорректированные значения дефицита уровня добычи до конца планового периода:
Аналогично вычисляются значения всех этих величин на последующие промежутки планирования. Итак, обобщая сказанное, выпишем общие рекуррентные формулы, составляющие экономико-математическую модель, по которым вычисляются основные технологические показатели процесса прироста извлекаемых запасов нефти и добычи.
Предположим, что
вычислены скорректированные, после ввода в разработку 
числа извлекаемых запасов с объемами 
, значения дефицита
уровня добычи нефти:
где 
- прогнозное значение добычи нефти
из извлекаемых запасов 
за i-й
промежуток планирования.
Допустим, что уровень
добычи из этих 
числа
извлекаемых запасов полностью восполняет первоначальный дефицит за период 
и пусть в 
-ом промежутке планирования 
образуется дефицит
уровня добычи нефти, т. е. 
для 
и 
. Тогда, для восполнения этого дефицита с начала 
го промежутка, т. е. с
момента времени 
,
необходимо ввести в разработку извлекаемые запасы, объем которых вычисляется по
формуле:
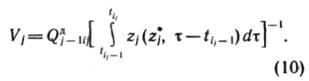
Прогнозные значения
уровня добычи из запасов 
за последующие промежутки планирования вычисляются
по формуле:
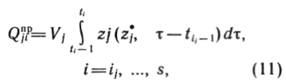
причем, очевидно, что 
.
Ввод дополнительных
извлекаемых запасов продолжается до 
го (p<=s) промежутка планирования включительно, когда добыча нефти
из запасов Vp полностью
восполнит дефицит до конца планового периода, т. е.
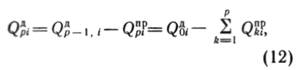
причем 
для всех 
Итак, нами приведены
рекуррентные формулы (9) - (11) для вычисления дефицита 
, уровня добычи 
,
и объемов извлекаемых запасов 
, которые с целью восполнения
первоначального дефицита добычи необходимо ввести в разработку в моменты
времени 
с законами
изменения темпа отбора нефти из них 
со значениями максимального темпа отбора 
соответственно. Здесь 
- множество допустимых
значений максимального темпа отбора нефти, которое принято в виде:
Очевидно, что при каждом
наборе значений параметров 
будут получаться цепочки из р - числа значений
объемов извлекаемых запасов 
и кривых изменения добычи 
из этих запасов. Выбор среди них оптимальной
осуществляется по следующему критерию:
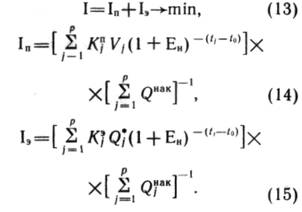
Здесь 
- отнесенные к единице добываемой
в плановом периоде продукции дисконтированные капитальные вложения,
соответственно, суммарные, на разведку и разработку; 
- накопленная за весь
плановый период добыча нефти (газа) из извлекаемых запасов 
; 
- максимальный в плановом периоде уровень
добычи из запасов 
;
Ен- нормативный коэффициент приведения разновременных затрат; 
- соответственно, коэффициенты
капитальных затрат на подготовку 1 т. извлекаемых запасов и на 1 т.
максимальной годовой добычи нефти (газа) из новых запасов.
Коэффициенты удельных
капитальных затрат 
и
в плановом периоде
могут расти с усилением сложности горно-геологических условий и уменьшаться с
ускорением НТП (в поисково-разведочных работах в технике и технологии
геофизических исследований и разведочного бурения, автоматизация интерпретации
геофизических данных и т. д.) и в отдельных процессах разработки месторождений
(строительство скважин и морских платформ; обустройство промыслов, техника и
технология добычи, сбор и транспорт продукции и т. д.). Известно, что с ростом
максимального темпа отбора 
растут и капвложения на разработку,
следовательно, и 
.
Итак, вышесказанное позволяет предложить следующие выражения для определения
коэффициентов удельных капитальных затрат:
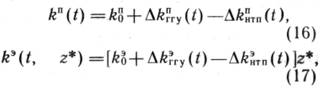
где 
- соответственно значение 
и 
к началу периода планирования, т.
е. при 
, 
коэффициенты, в
совокупности учитывающие соразмерно рост удельных капитальных вложений с
повышением сложности горно-геологических условий (ГГУ) и уменьшение их с
ускорением НТП. Прогнозные значения этих коэффициентов устанавливаются с
использованием данных ретроспективного анализа развития поисково-разведочных
работ и нефтегазодобычи в регионе и различных долгосрочных целевых программ НТП.
Таким образом, описанная
экономико-математическая модель, в соответствии с которой задача оптимального
планирования прироста запасов нефти (газа) и добычи из них заключается в
нахождении таких объемов новых запасов 
и добычи из них 
, а также параметров 
, при которых значение функционала I было бы минимальным.
Для численного решения рассмотренной задачи с помощью метода динамического программирования был разработан алгоритм, который реализован в виде программы на языке ФОРТРАН. Для простоты в рассматриваемом ниже примере принимается, что отбор нефти (газа) из всех начальных запасов V0 ведется с одинаковым темпом:
а из новых извлекаемых запасов 
с различными темпами:
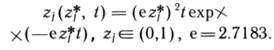
Предполагается также, что
коэффициенты удельных капитальных затрат 
и 
во времени изменяются по линейному закону:
Были проведены расчеты в
широком диапазоне изменения исходных параметров 
, а также законов изменения темпа отбора 
и коэффициентов
удельных капитальных затрат 
и 
. На основе анализа всех полученных результатов, в частности,
приведенных в таблице для данных: 
= 4 млн. т; V0
= 80 млн. т; 
= 2
руб/т; 
=2 500 руб/т;
s = 20,10,4; 
=-0,025;0,0; 0,025; Т = 20 лет; 
= -0,025; 0,0; 0,025 были
выявлены наиболее характерные особенности исследуемого процесса. Несмотря на
то, что расчеты проводились для самого простого случая изменения 
и 
без их структурной дифференциации, можно
отметить следующие основные моменты.
В плановом периоде, если
эффект НТП будет преобладать над отрицательным влиянием ГГУ, вследствие чего
коэффициенты 
и 
будут уменьшаться во
времени с одинаковыми или же с различными темпами, оптимальное развитие
подсистемы «Разведка - разработка» обеспечится при наименьших величинах
приходящихся на единицу добываемой в плановом периоде продукции капитальных
затрат как общих I, так и отдельных на
разведку и разработку. При этом, если изменение 
происходит более высоким темпом, чем 
, нормальное развитие
обеспечивается при меньших величинах снабжения добычи запасами 
, т. е. при относительно меньших
объемах, вводимых в разработку новых извлекаемых запасов за весь плановый
период 
или же в
отдельных его промежутках 
со сравнительно высоким максимальным темпом отбора 
и коэффициентом
использования новых запасов. Если же в плановом периоде происходит увеличение
обоих коэффициентов, то естественно, наблюдается обратное.
В общем случае, когда
направления темпов изменения коэффициентов 
и 
не совпадают, т. е. При уменьшении (увеличении)
одного из коэффициентов другой либо увеличивается (уменьшается), либо остается
постоянным, трудно сделать однозначные выводы. Между тем, достаточно четко
выражено более существенное влияние изменения в плановом периоде коэффициента 
на экономические и
технологические показатели долгосрочного планирования. Следовательно,
варьируя темпом ускорения НТП в отдельных процессах нефтегазодобычи при
установившейся тенденции изменения ггу можно выбрать наиболее рациональный путь
развития добычи нефти (газа) в регионе, а также установить приемлемые с точки
зрения реализации темпы ускорения НТП и уточнить объемы заданий для новой
техники и технологии.
Таким образом, предлагаемая модель прогнозирования на весь плановый период и на отдельные его промежутки оптимальных объемов прироста новых извлекаемых запасов нефти (газа) и добычи из них позволяет для конкретных условий на основе учета ускорения НТП в отрасли, региональных структурных особенностей (плановые задания, качество запасов, горно-геологические условия, дифференциация планового периода и т. д.) значительно улучшить и повысить надежность технико-экономических показателей долгосрочного планирования.
СПИСОК ЛИТЕРАТУРЫ
1. Желтов Ю.П. О математическом моделировании использования запасов полезных ископаемых / Экономика и математические методы.- 1971.-Т. VII.-Вып. 1.-С. 60-68.
2. Вопросы совершенствования планирования и экономического механизма управления отраслью / Труды ВНИИОЭНГ, вып. 32, М„ 1977.
3. Методы оптимального планирования добычи нефти.- М.: Наука.- 1978.
4. Определение уровней добычи газа на длительную перспективу / Гриценко А.П., Ермаков В.Н., Жабрев И.П. и др. // Газовая промышленность.- 1982.-№ 10.-С. 8-10.
5. Прогнозирование геолого-экономического качества ресурсов нефти и газа.- М.: Наука.- 1985.
6. Саттаров М.М., Гужновский А.Л. Обоснование оптимальных условий развития нефтяной промышленности / Экономика и управление нефтяной промышленности.- 1985.- № 8.- С. 30-34.
Таблица Оптимальное значение основных показателей прогноза за весь плановый период
|
Показатели |
|
|
||||||||
|
0,025 |
0,0 |
-0,025 |
||||||||
|
s=20 |
s= 10 |
s=4 |
s=20 |
s=10 |
s=4 |
s=20 |
s=10 |
s=4 |
||
|
I, руб/т |
0,025 |
15,8 |
20,5 |
30,8 |
15,1 |
19,7 |
29,7 |
14,3 |
18,4 |
28,5 |
|
0,0 |
14,5 |
18,8 |
28,2 |
13,8 |
18,2 |
27,2 |
13,2 |
17,4 |
26,1 |
|
|
-0,025 |
12,8 |
16,9 |
25,0 |
12,2 |
16,3 |
24,1 |
11,7 |
15,7 |
23,2 |
|
|
Iп, руб/т |
0,025 |
5,9 |
7,8 |
13,1 |
5,6 |
7,5 |
12,1 |
5,4 |
7,1 |
11,5 |
|
0,0 |
5,6 |
7,3 |
11,6 |
5,3 |
7,0 |
11,1 |
5,1 |
6,6 |
10,4 |
|
|
-0,025 |
5,2 |
6,6 |
10,0 |
4,9 |
6,3 |
9,6 |
4,7 |
6,0 |
9,1 |
|
|
Iэ, руб /т |
0,025 |
9,9 |
12,7 |
17,7 |
9,5 |
12,2 |
17,6 |
8,9 |
11,7 |
17,0 |
|
0,0 |
8,9 |
11,5 |
16,6 |
8,5 |
11,2 |
16,1 |
8,1 |
10,8 |
15,7 |
|
|
-0,025 |
7,6 |
10,3 |
15,0 |
7,3 |
10,0 |
14,5 |
7,0 |
9,6 |
14,1 |
|
|
|
0,025 |
80,3 |
106,2 |
176,6 |
82,6 |
110,3 |
179,5 |
87,2 |
115,2 |
186,0 |
|
0,0 |
75,8 |
99,1 |
156,1 |
78,3 |
102,3 |
163,7 |
81,5 |
106,7 |
168,6 |
|
|
-0,025 |
70,4 |
90,1 |
135,3 |
72,3 |
92,6 |
140,8 |
74,9 |
96,1 |
147,1 |
|
|
Коэффициент использования, % |
0,025 |
36,6 |
27,7 |
16,7 |
35,7 |
26,7 |
16,4 |
33,8 |
25,6 |
15,8 |
|
0,0 |
38,9 |
29,7 |
18,9 |
37,6 |
28,8 |
18,0 |
36,1 |
27,6 |
17,5 |
|
|
-0,025 |
41,8 |
32,7 |
21,8 |
40,7 |
31,8 |
20,9 |
39,3 |
30,6 |
20,0 |
|
