К оглавлению	УДК 539.217.1:553.98.061.4
	© В. М. Добрынин, 1991

Изучение пористости сложных карбонатных коллекторов

В.М. ДОБРЫНИН (МИНГ)

Комплекс двух методов пористости. В статье дано теоретическое обоснование способа изучения порово-трещинно-кавернозных коллекторов с помощью двух методов пористости (акустического и нейтронного, или акустического и гамма-гамма методов) и способа двух растворов в варианте акустического метода. Приведенные палетки построены теоретически с настройкой на карбонатные коллекторы месторождения Тенгиз, где они были опробованы с положительными результатами. Эти же способы могут быть использованы для построения палеток и для терригенных глинистых и трещинно-кавернозных коллекторов.

В гетерогенных средах с высокими показателями поглощения упругих волн существует объемная дисперсия скоростей, т. е. увеличение скорости волн с частотой. Однако исследования Ф.М. Ляховицкого [2] показывают, что применительно к горным породам величина максимальной дисперсии невелика. Для скорости поперечных волн в нефте- и водонасыщенных породах максимальная дисперсия существенно ниже 2 %, а для скорости продольных волн в тех же породах не превышает 3. В газонасыщенных породах дисперсия еще меньше. В низкопористых изверженных и крепко сцементированных породах дисперсия упругих волн практически не наблюдается.

Таким образом, если пренебречь дисперсией скоростей упругих волн в ультразвуковом диапазоне частот, то для описания кинематических характеристик поля упругих волн в многофазных моделях сред со сложным поровым пространством можно использовать обычные уравнения для скорости сплошных упругих тел. Однако в этих уравнениях должны быть учтены упругие характеристики (сжимаемость, плотность и коэффициент Пуассона), типичные для рассматриваемых горных пород. Наиболее сложным является определение коэффициента сжимаемости таких моделей.

На величину коэффициента сжимаемости влияют такие важнейшие факторы, как соотношение упругости скелета породы и порозаполняющих флюидов, структурно-литологические особенности породы и величина эффективного механического напряжения, которое испытывает порода на глубине ее залегания.

Воспользуемся понятием об изотермическом коэффициенте объемной сжимаемости  пористого тела [2]:

где V - объем тела; р - среднее нормальное напряжение (давление), испытываемое пористым телом на глубине его залегания; Т - температура.

Если учесть достаточно высокое гидравлическое сопротивление порового пространства у большинства сцементированных горных пород в естественном залегании, а также кратковременность действия колебательных напряжений (20-30 кГц), то можно допустить, что в пористых породах насыщающий ее флюид не может перетекать из одной поры в другую за время действия таких знакопеременных нагрузок. Следовательно, в этом случае поры можно рассматривать гидравлически изолированными друг от друга. Это предположение не является строгим и не может быть использовано для изучения динамических характеристик среды (затухания упругих волн), требующего учета влияния неравновесных термодинамических процессов в поровом пространстве породы. Однако при изучении кинематических характеристик (скорости упругих волн) это допущение можно принять, если учесть низкую дисперсию упругих волн.

В пористом теле с системой гидравлически замкнутых пор изотермическое изменение объема пор  под влиянием изменения среднего нормального напряжения dp должно быть равно изотермическому изменению объема заполняющего поры флюида - жидкости

Полный вывод уравнения для  с помощью допущения (2) приведен в работе [1]. Его окончательный вид таков:

где к_п - общая пористость;- коэффициенты сжимаемости соответственно пор породы, насыщающей жидкости и твердой фазы скелета;- коэффициент, учитывающий влияние сжимаемости включений (глинистых или других) в порах породы.

В частном случае для породы, не содержащей в порах глинистые или другие упругие включения,  =1, и уравнение (3) переходит в известное уравнение Ф. Гассмана (1951 г.).

Уравнение (3) можно также преобразовать к виду

Или, обозначив  получим

где- коэффициент упругой связи между фазами в породе, который для сцементированных пород может изменяться от 0,1 до 1.

Подставив полученное значение  в известные уравнения для скоростей упругих волн, будем иметь:

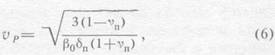
Или для интервального времени

где- коэффициент Пуассона,- плотность породы.

На рис. 1 изображены зависимости , рассчитанные по уравнению (6) для насыщенных минерализованной водой пород. Параметром этих кривых служит коэффициент сжимаемости пор

Коэффициент Пуассона изменяется в меньшей степени, чем коэффициент сжимаемости пор. При вычислениях было принято, что  варьирует: для известняков и доломитов от 0,30 (кальцит) до 0,35 (высокопористые разности), для песчаников от 0,10 (кварц) до 0,20 (высокопористые разности).

 для доломитов, известняков и песчаников приняты соответственно равными 1,16*10^-5, 1,34*10^-5 и 2,5*10^-5 МПа^-1.

Этим значениям  соответствуют: 142, 150 и 164 мкс/м. Коэффициент сжимаемости минерализованной воды

Плотности твердой фазы  для доломитов, известняков и кварцевых песчаников приняты соответственно равными 2,80*10³, 2,71*10³ и 2,65*10³ кг/м³.

На рис. 1 также изображены лабораторные данные изучения  на образцах разных пород с межзерновой пористостью, полученные в условиях, приближающихся к пластовым (эффективное напряжение 40-50 МПа), соответствующим глубинам залегания пластов около 3000-4000 м. При таких высоких напряжениях коэффициент сжимаемости пор пород с межзерновым типом пористости  почти на зависит от величины самой пористости [1]. Как видно из сопоставления, экспериментальные данные для доломитов с межзерновой пористостью приближенно осредняются кривой с параметром = 10*10^-5 МПа^-1, для известняков - кривой = 15*10^-5 МПа^-1 и для кварцевых низкоглинистых песчаников – кривой =20*10^-5 МПа^-1.

Усложнение строения порового пространства той же породы наличием трещин ведет к увеличению  породы, а при появлении каверн - к его уменьшению. Рассмотрим это явление подробнее.

Коэффициент сжимаемости породы, содержащей трещины каверны  и межзерновые поры, в общем виде определяется следующим выражением [1]:

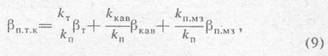
где Кт, Ккав, и Кп.мз - коэффициенты трещиноватости, кавернозности и межзерновой пористости соответственно:- коэффициенты сжимаемости трещин, каверн и межзерновых пор соответственно.

Для порово-трещинного типа коллектора уравнение (9) приобретает вид

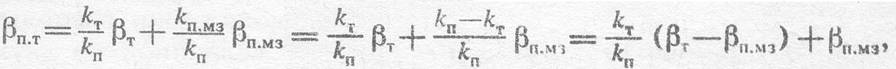
где- коэффициент сжимаемости пор порово-трещинного типа коллектора.

Посколькуто последнее равенство можно упростить:

Из работы [1] следует, что сжимаемость трещин можно оценить из условий прочности на сжатие минералов, заполняющих трещины.

где 25*10^-3 - коэффициент, полученный для мелкозернистого (золенгофенского) известняка, 135*10^-3 - то же для кварцита, р - среднее нормальное напряжение, р_пл - пластовое давление.

Мы не располагаем данными о прочности на сжатие рифогенных карбонатных образований. Поэтому в первом приближении воспользуемся средней арифметической величиной из двух крайних значений. Тогда

Для условий месторождения Тенгиз (h_ср=4500 м и P_пл=80 МПа) величина эффективного напряжения P-Рпл= 30 МПа. Для этого значения

что более чем на порядок выше коэффициента сжимаемости межзерновых пор (=15*10^-5 МПа^-1).

С учетом двух последних значений уравнение (10) примет вид

По этому уравнению можно рассчитать значение для различных величин к_т/к_п.

Для порово-кавернозной породы (к_т=0) уравнение (9) примет вид

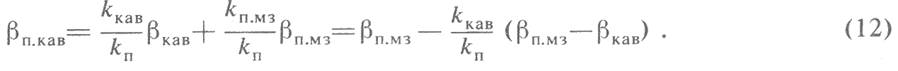
Теоретическая оценка показывает 11], что сжимаемость вторичных изометрических пор (каверн) равна

Где - сжимаемость вмещающей каверны породы (матрицы), содержащей гидравлически не сообщающиеся между собой поры; - коэффициент Пуассона матрицы.

Если принять для низкопористых карбонатных пород =0,3 Кп.мз=5%, =1,34*10^-5 МПа^-1, то при  и, согласно (13),~4*10^-5 МПа^-1.

Уравнение (12) в этом случае примет вид

Таким образом, как следует из рассмотрения уравнений (11) и (14), трещиноватость увеличивает коэффициент сжимаемости пор породы, а кавернозность уменьшает. Поэтому может возникнуть условие, при котором эти два фактора «уравновесят» друг друга.

Это условие «акустической прозрачности» можно записать:

Подставляя в это равенство значения  и  согласно уравнениям (10) и (12) и выполнив необходимые преобразования, для карбонатных пород получим:

Другими словами, коэффициент трещиноватости влияет на коэффициент сжимаемости в 23 раза больше, чем коэффициент кавернозности. Например, очень большая величина кавернозности (К_кав = 7 %) уменьшает сжимаемость пор пласта на такую же величину, на которую увеличивает ее трещиноватость с коэффициентом к_т- 0,3 %, т.е. одновременное наличие в пласте кавернозности и трещиноватости в определенных соотношениях может быть не замечено интерпретатором. Уменьшить эту неоднозначность можно, используя при интерпретации коэффициент затухания продольных волн.

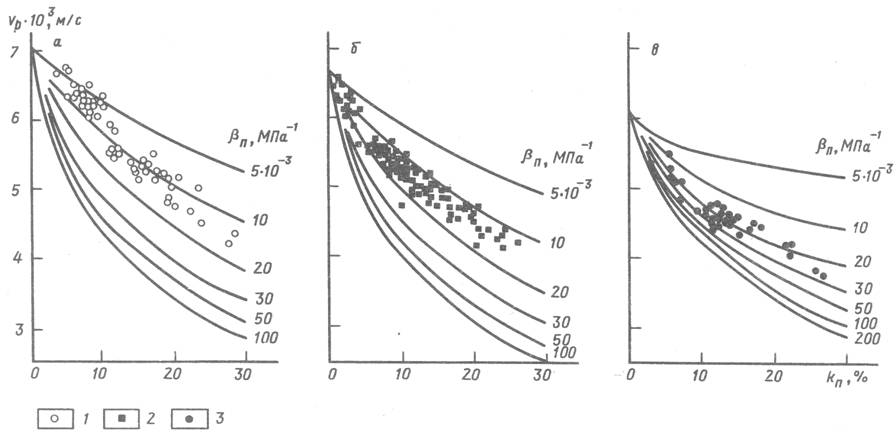
На рис. 2 изображены теоретические зависимости между интервальным временем  и общей пористостью к_п карбонатных пород, вычисленные по уравнениям (8), (11) и (14).

Рассмотренные палетки позволяют по данным двух геофизических методов (акустического и нейтронного, или гамма-гамма, методов) оценить межзерновую пористость или долю трещин и каверн в общей пористости в более сложном карбонатном коллекторе.

Следует иметь в виду, что  могут изменяться в зависимости от глубины залегания и типа породы. Это «настроечные» контакты в уравнении. Именно таким путем построены на рис. 2 палетки для доломитов и доломитизированных известняков месторождения Тенгиз.

Способ двух растворов в варианте акустического метода исследования скважин. Этот способ основан на значительном различии коэффициентов сжимаемости легкой нефти и фильтрата бурового раствора на водной основе (РВО). Выполняются два исследования акустическим методом: вначале при вскрытии пласта на нефильтрующемся буровом растворе (ИБР или РНО), а затем после замены ИБР на РВО. В зоне проникновения фильтрата бурового раствора происходит вытеснение нефти из проницаемых пластов. Это приводит к различию в показаниях акустического метода.

Согласно уравнению (8) отношение показаний прибора в рассматриваемых случаях можно представить в виде

Где  и - объемные коэффициенты сжимаемости соответственно нефтенасыщенного пласта и того же пласта в зоне проникновения фильтрата раствора; - плотности нефтенасыщенного пласта и того же пласта в зоне проникновения.

Уравнение (4) при сложном составе заполняющего поры флюида можно записать:

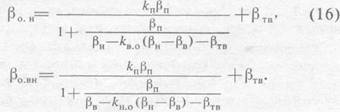
Плотность пластов также изменится:

где- плотности нефти, воды и минералов (твердой фазы) пласта,- коэффициенты остаточной водо- и нефтенасыщенности.

По уравнениям (15), (16) и (17) можно рассчитать величину отношенияв зависимости от коэффициента пористости и типа коллектора и представить ее в виде ,%.

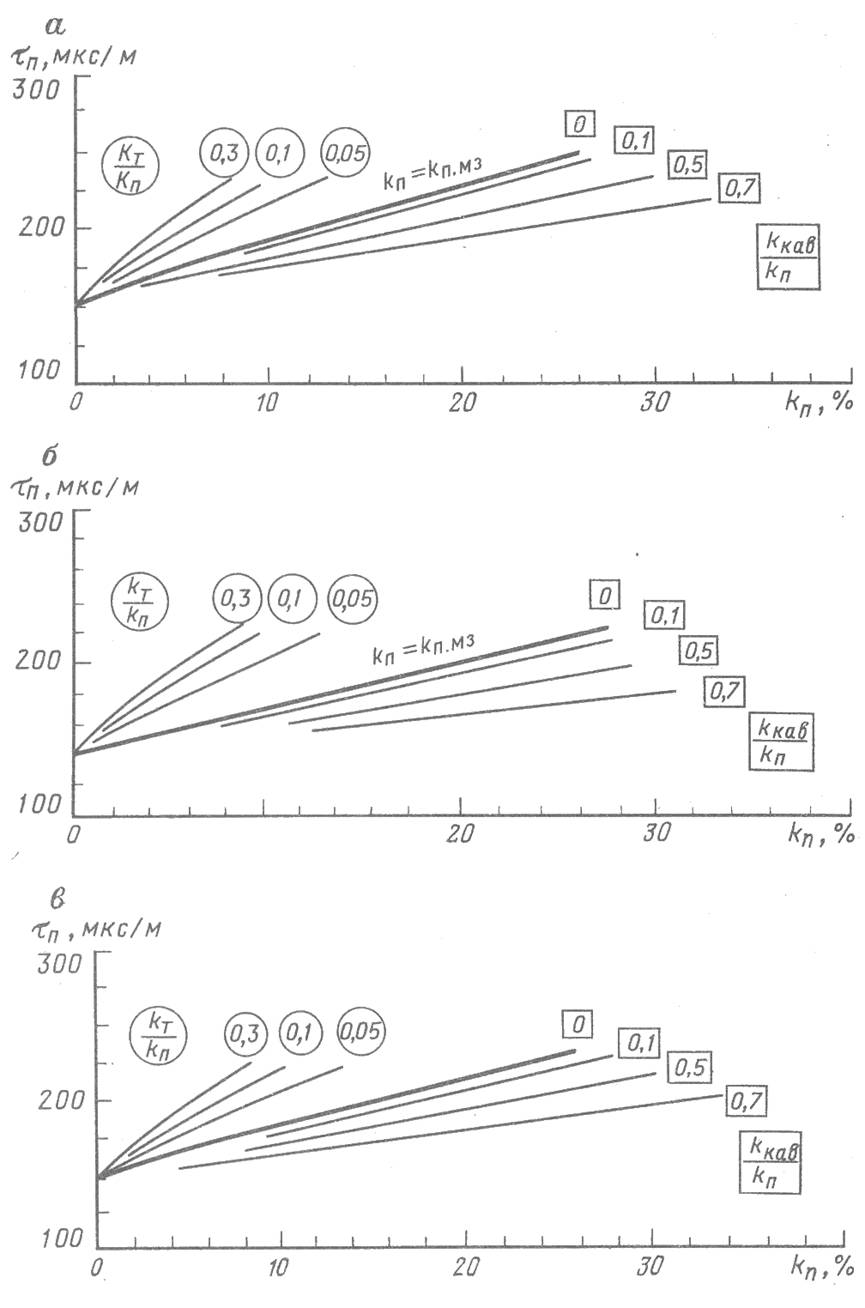
На рис. 3 представлены результаты этого расчета для условий месторождения Тенгиз: = 15*10^-5;= 185* 10^-5 МПа^-1 при T=107°С и р_пл=80 МПа (данные А.И. Брусиловского, 1990 г.); = 30*10^-5 МПа^-1,==0,66*10³,=1,1*10³ кг/м³, 0,06<K_BO<0,20. Сжимаемость нефти почти на порядок выше сжимаемости воды.

На полученной палетке четко выделяются четыре зоны: I - преимущественно трещинные коллекторы, II - преимущественно межзерновые коллекторы, III - порово-кавернозные коллекторы и IV - практически непроницаемые породы (Кно>0,40-0,50), возможно, битуминозные, вязкие нефти.

Учитывая, что эффект изменения интервального времени обусловлен проникновением в пласт фильтрата водного бурового раствора, на этой палетке можно приближенно наметить зоны высокой и низкой проницаемости пород.

Для зоны трещинных коллекторов используется известное уравнение для проницаемости пласта с системой линейных трещин трех взаимно перпендикулярных направлений:

где к_пр- коэффициент проницаемости, мкм²; b - величина раскрытости микротрещин в шлифах, мкм.

Если принять, что наиболее часто встречающиеся величины b, по данным разных авторов, в шлифах карбонатных пород составляют около 15 мкм, то получим приближенную связь проницаемости микротрещиноватых пород с коэффициентом трещиноватости

Зная величину к_т/к_п и значение к_п, по уравнению (19) можно в зоне трещинных коллекторов наметить области более высокой и более низкой проницаемости.

В зоне межзерновых коллекторов также возможно выделить области высоких и низких проницаемостей. Для этого используют корреляционную связь между Кво и Кп для месторождения Тенгиз и связь между Кпр и Кво для биоморфных известняков (Б.Н. Тульбович, 1979 г.).

Ниже зоны межзерновых коллекторов на палетке располагается зона порово-кавернозных пород, характеризуемая более высокими значениями Кно. В этих породах проникновение фильтрата затруднено, что свидетельствует о более низкой их проницаемости и более сложной структуре порового пространства. С данным обстоятельством связано и уменьшение коэффициента вытеснения нефти в этих породах.

Рассмотренные в настоящей статье способы изучения пористости коллекторов сложного строения были опробованы при изучении карбонатных коллекторов нефтяного месторождения Тенгиз (см. статью Н.В. Фармановой и В.А. Костериной в настоящем номере журнала) и при изучении юрских терригенных коллекторов Талинского нефтяного месторождения.

СПИСОК ЛИТЕРАТУРЫ

1. Добрынин В.М. Деформации и изменения физических свойств коллекторов нефти и газа.- М.: Недра.-1970.

2. Ляховицкий Ф.М. Сейсмические волны в гетерогенных средах. - М.: Изд. МГК АН СССР,- 1988.

Abstract

In this paper, we present a theoretical substantiation of our studies of cavernous-porous-fractured reservoirs with the help of two porosity methods (acoustic plus neutron or gamma methods) and by means of two solutions in a variation of the acoustic technique. Theoretical empirical charts provided are "set" to the conditions of investigating carbonate reservoirs of the Tengiz field where they have been successfully tested.

Рис. 1. Сопоставления теоретических зависимостей  с лабораторными определениями скорости и пористости кернов, насыщенных минерализованной водой (250 г/л) доломитов (а), известняков (б) и песчаников (в).

Шифр кривых: коэффициент сжимаемости пор, МПа^-1 Образцы в пластовых условиях: 1 - доломитов (по В.П. Потапову, И.С. Жуковой и др., 1973 г.); 2 - известняков (по данным тех же авторов); 3 - кварцевых песчаников (по В.М. Добрынину, Г.М. Авчяну и др., 1988 г.)

Рис. 2. Теоретические зависимости  для карбонатных пород с межзерновой (), порово-трещинной (в квадратах) и порово-кавернозной  пористостью (в кружках) и для водонасыщенных или продуктивных пород, вскрытых скважинами на РВО

а - известняки, б - доломиты, в - доломитизированные известняки

Рис. 3. Теоретические зависимости приращения интервального времени,%, от пористости к_п, остаточной нефтенасыщенности пласта в зоне проникновения к_но (в квадратах) и трещиноватости к_т/к_п (в кружках) известняков Тенгизского месторождения:

Пунктирные линии - линии равной проницаемости, к_пр-10 мкм²