К оглавлению	УДК 550.832
	© Коллектив авторов, 1991

Оценка характеристик зондов бокового микрокаротажа

А.Г. Барминский, Р.А. Кучеров, Н.И. Танцуренко, Ю.Я. Толмачев (нииги)

В комплексе геофизических исследований скважин на месторождениях нефти и газа видное место занимает боковой микрокаротаж (БМК), который позволяет оценить величину удельного электрического сопротивления прискважинной части пласта, что имеет важное значение для выяснения геологической характеристики пласта и его газонасыщения. Определение зависимостей показаний зондов БМК от параметров глинистой корки, зоны проникновения и неизменной части пласта является сложной задачей. Для оценки свойств БМК могут быть применены следующие методы: моделирование на электрических сеточных и электролитических моделях, а также математическое моделирование.

Моделирование на электрических сеточных моделях основано на замене изучаемого пространства, образованного скважиной и горными породами, плоской сеткой и успешно применяется при изучении осесимметричных задач электрического каротажа. Однако электрические сеточные модели трудно реализуемы для задач с нарушением осевой симметрии.

Обычно оценку свойств зондов БМК проводят на электролитических моделях, в которых среды с различным удельным электрическим сопротивлением заменяются растворами соответствующей концентрации, разделенными мембраной. Недостатками электролитических моделей являются сложность реализации электропроводящей мембраны и низкая в связи с этим точность моделирования.

Математическое моделирование для исследования характеристик зондов БМК стало использоваться лишь в самое последнее время. При этом, чем ближе математическая модель к реальному зонду, тем сложнее программа расчета на ЭВМ. Кроме того, при математическом моделировании трудно учесть контактное сопротивление электродов микроустановок.

Авторами разработана методика комбинированного способа расчета характеристик зондов БМК. Способ расчетно-экспериментальный, основан на использовании теоретической зависимости показаний зонда от удельного сопротивления породы при отсутствии глинистой корки на стенке скважины и результатов электролитического моделирования зонда в скважине и бесконечно высоком значении удельного сопротивления породы. Модель проста и представляет собой отрезок трубы из изоляционного материала диаметром 200 или 250 мм и высотой 1200 мм.

Известно, что основное искажающее влияние на показания зонда БМК оказывают удельное сопротивление  и толщина  слоя глинистой корки и промывочной жидкости между лицевой поверхностью электродов зонда и стенкой скважины. При отсутствии или малой толщине промежуточного слоя кажущееся удельное сопротивление равно удельному сопротивлению пласта или промытой зоны (). Информативным оказалось исследование зондов в упрощенной модели, когда скважину заменяют трубой из изоляционного материала. В этом случае моделируется одна среда - скважина с удельным сопротивлением. Удельное сопротивление пласта равно бесконечности. Регистрируемые значения кажущихся сопротивлений при заданной толщине промежуточного слоя являются предельными и могут использоваться для сравнения изучаемых зондовых установок.

Рассмотрим применяемый на практике двухэлектродный зонд БМК с равнопотенциальными центральным и экранным электродами. По измеренному значению тока центрального электрода при заданной толщине промежуточного слоя можно определить геометрический фактор промежуточного слоя. Геометрический фактор слоя по току центрального электрода определяется выражением

где- величина тока центрального электрода зонда при толщине промежуточного слоя h (мм), - величина тока центрального электрода зонда в однородной безграничной среде с удельным сопротивлением(в баке больших размеров при моделировании). Тогда геометрический фактор среды, расположенной вне слоя, равен

Отмеченные выражения позволили перейти к расчетно-экспериментальной модели для изучения поведения микроустановок в двух средах: скважине с удельным сопротивлением  и породе с удельным сопротивлением. В этом случае ток центрального электрода зонда определяется по формуле

где U₀ - потенциал системы электродов зонда при толщине промежуточного слоя, равной нулю; k - коэффициент зонда. Величина, обратная получаемому значению кажущегося удельного сопротивления, определяется выражением

где- потенциал системы электродов зонда при толщине промежуточного слоя, равном h. В формуле (4) все величины, за исключением, измеряются на упрощенной модели или задаются (). Также на упрощенной модели замеряются потенциал системы электродов зонда при толщине промежуточного слоя, равной нулю, и потенциал при толщине промежуточного слоя, равной h мм .

В реальных условиях потенциал U₀ изменяется от  при  до  при , а потенциал изменяется от  при до при . Диапазон изменения указанных потенциалов для реальных зондовых установок мал и не превышает двух. Поэтому для задаваемых значенийони могут быть рассчитаны по следующим приближенным формулам:

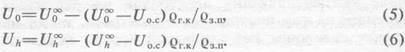
Кажущееся сопротивление для любых установленных значений  рассчитывается как обратная величина выражения (4) по измеренным в упрощенной модели значениям  и измеренным в баке большого размера значениям . Опыт показал, что для зондовых установок БМК, имеющих малую глубинность исследования, достаточно использовать бак диаметром 1200 и высотой 2000 м.

Предложенная методика оценки характеристик зондом БМК по результатам их испытания в упрощенной модели среды позволила перебрать много вариантов зондов в различных скважинных условиях. В результате работы предложен новый зонд БМК, который назван зондом компенсированного бокового каротажа (КБМК) в связи с используемым эффектом компенсации тока центрального электрода [2]. Этот зонд содержит изоляционный башмак, прижимаемый к стенке скважины. На рабочей поверхности башмака расположены центральный, экранный и два небольшого размера компенсирующих электрода, находящихся по вертикали симметрично относительно центрального и отделенных от экранного электрода тонким изоляционным промежутком. Потенциалы центрального и экранного электродов одинаковы. Потенциал компенсирующих электродов с помощью простой резистивной схемы автоматически устанавливается выше потенциала экранного электрода. Локальное поле компенсирующих электродов не оказывает влияния на ток центрального электрода, когда на стенке скважины нет глинистой корки. Когда на стенке скважины появляется глинистая корка, поле этих электродов оказывает компенсирующее влияние на величину тока центрального электрода, что снижает влияние глинистой корки на показания зонда по сравнению с обычным двухэлектродным зондом БМК.

Недостатком предложенной методики является то, что она не позволяет оценить глубинность зондов. Авторами разработана также программа расчета поля зондов БМК на ЭВМ при наличии в скважине глинистой корки и зоны проникновения в пласты. При этом использовался метод вторичных зарядов [1]. Тогда потенциал токовых электродов

где L - расстояния от точек, определяющих положения зарядов, до точки наблюдения а; - плотность зарядов на токовых электродах ;- плотность зарядов, индуцированных на поверхности изолятора башмака зонда .

А напряженность на поверхности изолятора будет равна:

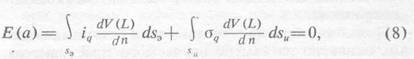
где V(L) выражение для потенциала точечного источника, смещенного с оси скважины [3].

При математическом моделировании сечение зонда плоскостью z=const было представлено в виде части сектора с углом  при вершине, заключенной между дугами концентрических окружностей с радиусами r₁ и r₂, центр которых совпадает с осью скважины, где r₁ - радиус внешней поверхности изолятора башмака, r₂ - радиус внутренней поверхности изолятора башмака. Центральный А₀ и экранный Аэ электроды расположены на внешней поверхности изолятора. Обратным электродом В является корпус прибора, который был представлен в виде тонкой проводящей нити достаточно большой длины (2,4 м), находящейся на оси скважины. Радиус цилиндрической поверхности электродов А₀ и А_э при расчетах принимался равным r₁. Поверхности электродов и изоляторов зонда разбивались плоскостями, проходящими через ось скважины, на 2k частей, плоскостями, перпендикулярными оси, на n частей с равным шагом  и Dz соответственно. Обратный электрод разбивался на N частей также с шагом Dz. Плотность зарядов принималась постоянной в пределах каждого элементарного участка поверхности электродов и изолятора.

Потенциал и напряженность определялись в середине каждого элемента поверхности зонда. В результате с учетом симметрии относительно плоскости  получалась система (3nk+N+2) алгебраических уравнений с таким же числом неизвестных, решая которую, определяли потенциал электродов А₀, А₃, В, ток центрального электрода и значение кажущегося удельного сопротивления .

На рис. 1, а приведены кривые поправочных коэффициентов за влияние глинистой корки на показания двухэлектродного зонда БМК серийной аппаратуры Э2, построенные по результатам расчетно-экспериментального метода и данным математического моделирования. Эти кривые представляют собой зависимости отношения удельного сопротивления зоны проникновения к кажущемуся сопротивлениюот отношения кажущегося сопротивления к удельному сопротивлению глинистой коркидля фиксированных значений толщины глинистой корки h. На рис. 1,б приведены аналогичные кривые для КБМК, имеющего как и зонд БМК поперечный размер 90 мм (увеличение ширины башмака зонда БМК и КБМК позволяет улучшить их характеристики по влиянию глинистой корки, но ограничивается требованием прохождения приборов в скважине). Данные математического моделирования хорошо совпадают с данными расчетно-экспериментального метода для двухэлектродного зонда БМК (см. рис. 1, а). Для зонда КБМК эти данные несколько отличаются между собой (в пределах 10 %). Это может быть вызвано влиянием контактного сопротивления электродов, которое не учитывалось при математическом моделировании, некоторым несовершенством математической модели зонда и экспериментальной модели среды, а также погрешностями экспериментальных измерений. На рис. 2 приведены псевдогеометрические факторы зондов БМК и КБМК, построенные по данным математического моделирования, которые представляют собой зависимость

Из приведенных данных видно, что существенное уменьшение влияния глинистой корки на показания зонда КБМК достигнуто за счет лишь небольшого увеличения радиуса исследования этого зонда по сравнению с зондом БМК.

Таким образом, разработаны два различных метода оценки характеристик зондов БМК. Расчетно-экспериментальный метод позволил преодолеть сложности непосредственного моделирования двух сред, перебрать много вариантов зондов в различных скважинных условиях и в результате разработать новый зонд КБМК. Метод математического моделирования подтвердил правильность результатов, полученных расчетно-экспериментальным методом, и позволил оценить глубинность исследования зондов БМК. Дальнейшее совместное использование этих методов несомненно повысит как оперативность в проведении исследований новых зондов, так и достоверность полученных характеристик этих зондов.

СПИСОК ЛИТЕРАТУРЫ

1. Альпин Л.М. Источники поля в теории электроразведки// Прикладная геофизика,- М.: Гостоптехиздат,- 1947.- Вып 3.- С. 56-100.

2. Барминский А.Г., Кулигин А.А., Толмачев Ю.Я. Устройство бокового микрокаротажа скважин. А. с. 1075212 (СССР) Б. И,- 1984,- № 7.

3. Кулинкович А.Е. Решение задачи теории электрического каротажа в случае смещения источников поля с оси скважины // Прикладная геофизика.- М.: Гостоптехиздат.- 1962,- Вып. 32,-С. 122-131.

Abstract

Experimental and mathematical ways to calculate the characteristics of lateral micrologging sondes are considered. The curves of correction coefficients for the effects of wall mud cake on lateral micrologging sonde readings constructed from the results of mathematical modeling and an experimental means of calculating are shown. An estimate of depth of the investigation of the lateral micrologging sondes is given.

Рис. 1. Поправочные коэффициенты за влияние глинистой корки на показания зондов БМК прибора Э2 (а) и КБМК (б).

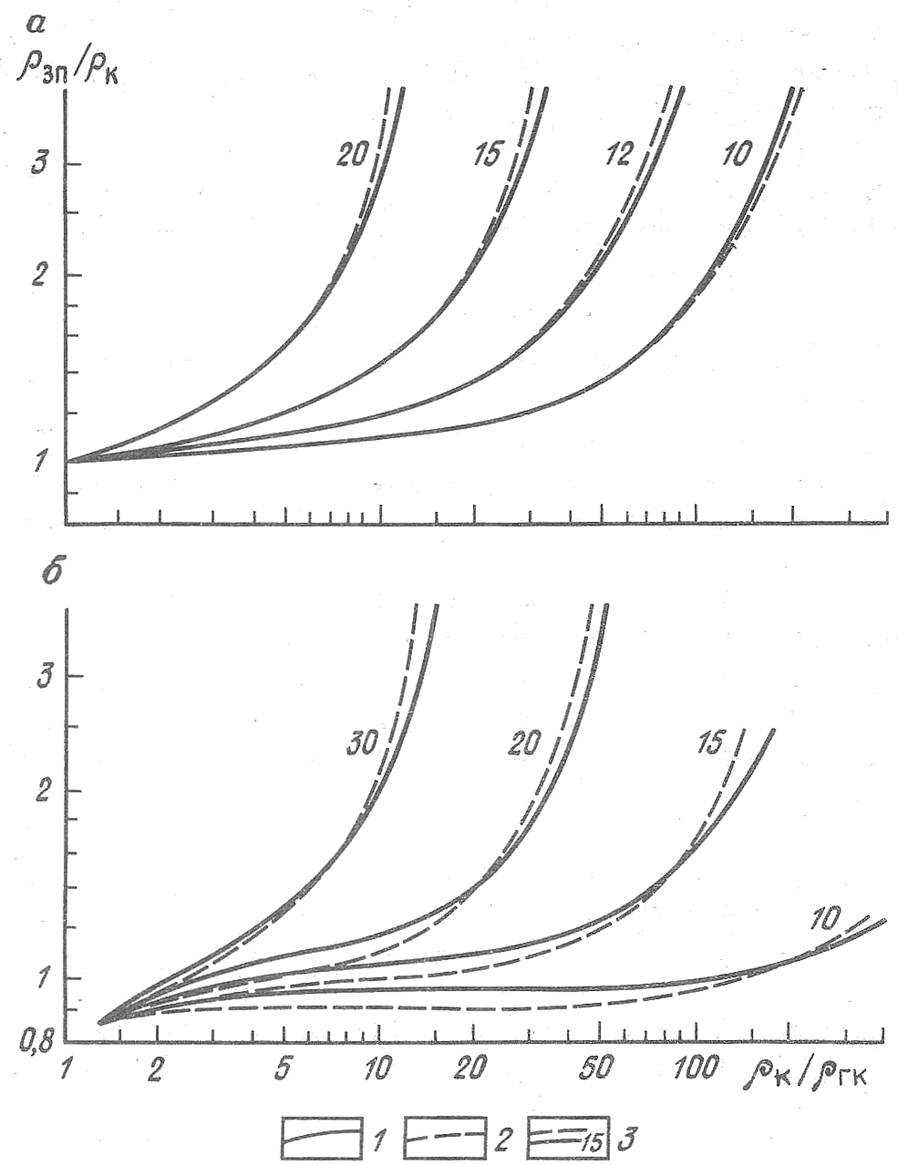
Кривые, построенные по результатам: 1 - расчетно-экспериментального метода, 2 - математического моделирования; 3 - толщина глинистой корки, мм

Рис. 2. Псевдогеометрические факторы зондов БМК и КБМК.

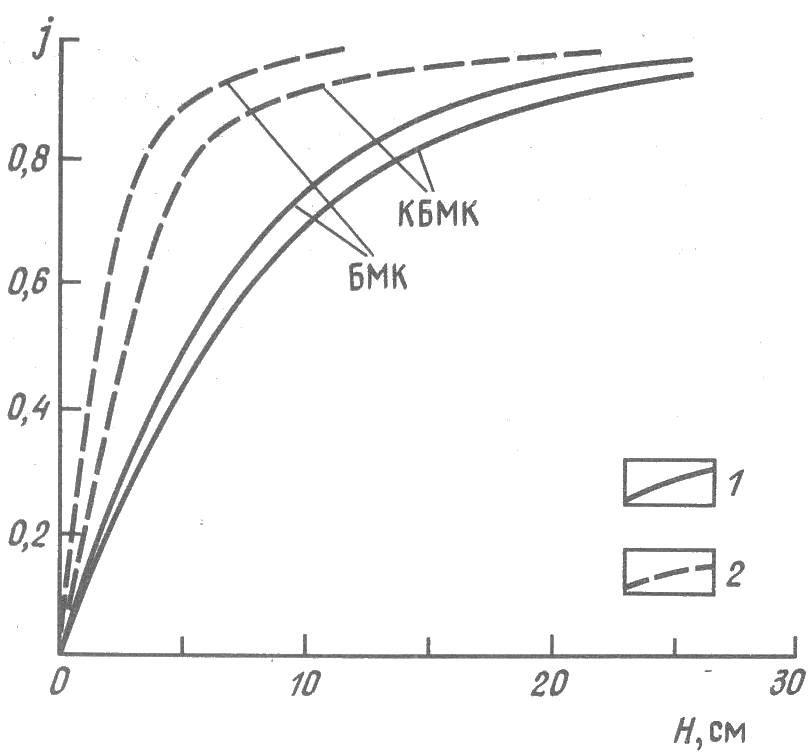
1 -; 2 -; Н - глубина проникновения, см