|
УДК 552.405.1+550.85 |
|
|
|
© P.X. Муслимов, Д. Б. Искандеров, 1991 |
Коррелируемость трещиноватости пород фундамента и выбуренного шлама
P. X. МУСЛИМОВ (Татнефть), Д. Б. ИСКАНДЕРОВ (ТВФ МИНГ)
Изучение залегающих под осадочным чехлом кристаллических пород фундамента, поиски в них скоплений УВ, термальных высоко минерализованных рассолов и вод, кондиционных концентраций редких элементов, благородных газов и других полезных ископаемых относятся к числу задач, решаемых современной глубинной геологией. Важнейшей из них является выяснение интервалов потенциального нахождения флюидов в разрезе кристаллических пород. Попытки ее решения предпринимаются, в частности, при бурении специальных скважин, в том числе и сверхглубоких, тем более что в последнее время возможность накопления и фильтрации флюидов при благоприятных условиях в фундаменте, судя по литературным данным, вовсе не исключается. Так, в работе [1] показана возможность обнаружения своеобразных ловушек для УВ на глубинах до 14 км, образованных сочетанием зон развития трещиноватых пород и арочно перекрывающих их плотных магматических и метаморфических покрышек.
С помощью бурения Новоелховской сверхглубокой скв. 20009 ведется поиск условий миграции и скоплений УВ и других флюидов в разрезе кристаллического фундамента Русской платформы. Однако из-за того, что отбор керна несплошной (трещиноватый керн интенсивней разрушается в керноприемной трубе), возникла идея о возможности выделения трещиноватых интервалов разреза сопоставлением качественных данных по кавернометрии и гранулометрии шлама. Такое предположение основано на том, что, с одной стороны, при прохождении трещиноватых пород выбуренный шлам является более крупным, нежели из соседних интервалов, сложенных монолитными породами, которые долотом тяжело и мелко истираются. С другой стороны, каверны в интервале фундамента образуются легче в трещиноватых породах, чем в монолитных. Следует оговориться, что часть крупных обломков в шламе образуется, особенно на значительных глубинах, за счет «отстреливания», т. е. разрушения отдельных участков пристеночной части вследствие упругости из-за уменьшения нагрузки на породы фундамента при их вскрытии. Однако характер обломков при разрушении долотом и за счет упругих сил различный. Так, частицы выбуренного шлама, как правило, изометрические по всем трем измерениям, а «отстрелянные» от стенок скважины экземпляры чаще всего плоские в виде пластин, толщина которых обычно не превышает 1-1,5 мм, а площадь нередко достигает нескольких квадратных сантиметров. Поэтому различать шлам того и другого происхождения не представляется сложным.
Для статистической проверки этой предпосылки была составлена корреляционная таблица (табл. 1), в которой сопоставляются качественные признаки: крупность шлама и характеристика ствола скважины по кавернометрии. Причем каждый образец шлама, отобранный при бурении с шагом в 1 м, при макроописании относится к одной из двух категорий: шлам считается крупным, если преобладающие размеры его обломков более 5 мм, и мелким - в случае преимущественного развития в нем частиц заметно менее 5 мм в поперечнике. Затем была дана оценка связи между этими признаками вдоль ствола скважины (рисунок) и рассчитана эта связь путем применения метода математической статистики (табл. 2).
Силу связи можно измерить с помощью коэффициентов связи [2]:
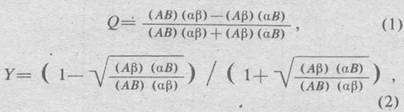
где А - наличие крупного шлама; В - наличие каверны в
стволе скважины, т. е. прохождение трещиноватых пород;
- наличие мелкого шлама; 
- отсутствие каверны в
стволе скважины, т. е. прохождение монолитных пород;
и т. д. представляют собой случаи попарного
совпадения перечисленных отдельных признаков.
Подставив результаты табл. 2 в формулы (1) и (2), вычислим оба коэффициента связи:
Q=(36*24-7*2)/(36*24+7*2)=0.98
По полученным значениям коэффициентов можно сделать вывод, что связь между крупностью шлама и кавернами в стволе скважины в его соответствующих интервалах сильная.
Коэффициент корреляции двух зависимых друг от друга качественных признаков А и В определяем по формуле
Подставив значения, получим 
Ввиду того, что коэффициент корреляции достаточно велик, можно сделать вывод: предпосылка о существовании связи выноса крупного шлама при бурении трещиноватых пород обоснована.
Для решения вопроса о том, насколько реально значение коэффициента корреляции и не определено ли оно одними только случайностями, рекомендуется вычислять среднюю квадратическую ошибку коэффициента корреляции [2] по формуле
где N - число наблюдений.
В нашем примере 
Если абсолютное значение коэффициента
корреляции не менее 
то
связь признаков реальная. Проверка 
убеждает, что это так.
Таким образом, статистическая обработка данных бурения Новоелховской скв. 20009 подтверждает наличие тесной связи между крупностью шлама и трещиноватостью пород соответствующих интервалов кристаллического фундамента. Этот вывод может быть полезен при выборе объектов испытания в разрезе подобных скважин.
СПИСОК ЛИТЕРАТУРЫ
1. Николаевской В.Н. Шведская сверхглубокая // Природа.- 1988,- № И.- С. 40.
2. Шарапов И.П. Применение математической статистики в геологии,- М.: Недра.- 1965.- С. 210-212.
A correlation of fractured zones of crystalline basement with a mode of cuttings carried up from the appropriate intervals is considered based on statistical data obtained from the investigation of the granulometry of cuttings and on the caliper logging data from the ultradeep well (Novo-Yelkhov No. 20009) being in drilling. A close link between coarsegrained cuttings and crystalline basement rock fracturing has been established by applying the method of mathematical statistics. The conclusion regarding the correlatability of these parameters may be used when selecting the test objects in similar wells.
Таблица 1. Корреляционная связь характеристик шлама и соответствующих интервалов ствола скважины
|
Образец |
Интервал отбора шлама, м |
Интервал ствола скважины по кавернограмме, м |
Порода |
Характеристика крупности шлама |
Характеристика соответствующего интервала ствола скважины |
|
1 |
1892 |
1892 |
Гранит розовый |
м |
н |
|
2 |
1895 |
1895 |
Мигматит |
м |
н |
|
3 |
1896-1897 |
1896-1897 |
Гнейс биотитовый |
м |
н |
|
4 |
1825 |
1924-1926 |
Гранитоид |
к |
Кв |
|
5 |
1938 |
1935-1945 |
» |
к |
Кв |
|
6 |
1941 |
1935-1945 |
» |
к |
Кв |
|
7 |
1947 |
1947-1952 |
Мигматит |
м |
н |
|
8 |
1951 |
1947-1952 |
» |
м |
н |
|
9 |
1968 |
1967-1975 |
Гранитоид |
к |
Кв |
|
10 |
2075 |
2075-2077 |
Мигматит |
к |
Кв |
|
11 |
2151 |
2150-2160 |
Гнейс биотитовый |
м |
Кв |
|
12 |
2236-2244 |
2230-2240 |
Гранитоид |
м |
н |
|
13 |
2325-2334 |
2225-2232 |
Гнейс биотит-пироксеновый |
к |
н |
|
14 |
2362 |
2358-2365 |
Гнейс гранат-биотитовый |
к |
Кв |
|
15 |
2392 |
2390-2410 |
» |
к |
н |
|
16 |
2407 |
2405-2410 |
» |
м |
н |
|
17 |
2465-2466 |
2460-2465 |
Гнейс биотит-пироксеновый |
к |
н |
|
18 |
2505-2511 |
2505-2511 |
Гнейс гранат-биотитовый |
к |
Кв |
|
19 |
2710-2715 |
2710-2715 |
Мигматит |
м |
Кв |
|
20 |
2794 |
2790-2802 |
Гранитоид |
к |
Кв |
|
58 |
4412-4430 |
4412-4430 |
Амфиболит |
к |
Кв |
|
59 |
4468 |
4440-4468 |
Гнейс гранат-биотитовый |
к |
Кв |
|
60 |
4481-4488 |
4480-4495 |
к |
Кв |
|
|
61 |
4504-4508 |
4500-4512 |
к |
Кв |
|
|
62 |
4511-4514 |
4500-4512 |
к |
Кв |
|
|
63 |
4517-4519 |
4515-4520 |
к |
Н |
|
|
64 |
4523-4528 |
4521-4528 |
к |
Кв |
|
|
65 |
4544-4562 |
4545-4562 |
Гнейс гранат-амфибол-биотитовый |
к |
Кв |
|
66 |
4564-4575 |
4564-4575 |
к |
Кв |
|
|
67 |
4576-4578 |
4576-4580 |
к |
Кв |
Примечание. Шлам: М - мелкий, К - крупный; Н - ствол скважины нормальный; Кв - каверна.
Таблица 2. Параметры расчета силы связи сопоставляемых признаков
|
Признаки |
B |
b |
Итого |
|||
|
А |
(АВ) |
36 |
(A b) |
7 |
(А) |
43 |
|
a |
(a В) |
2 |
(a b ) |
22 |
(a ) |
24 |
|
- |
(В) |
38 |
(b) |
29 |
|
67 |
Рисунок Пример сопоставления кавернограммы и шлама:
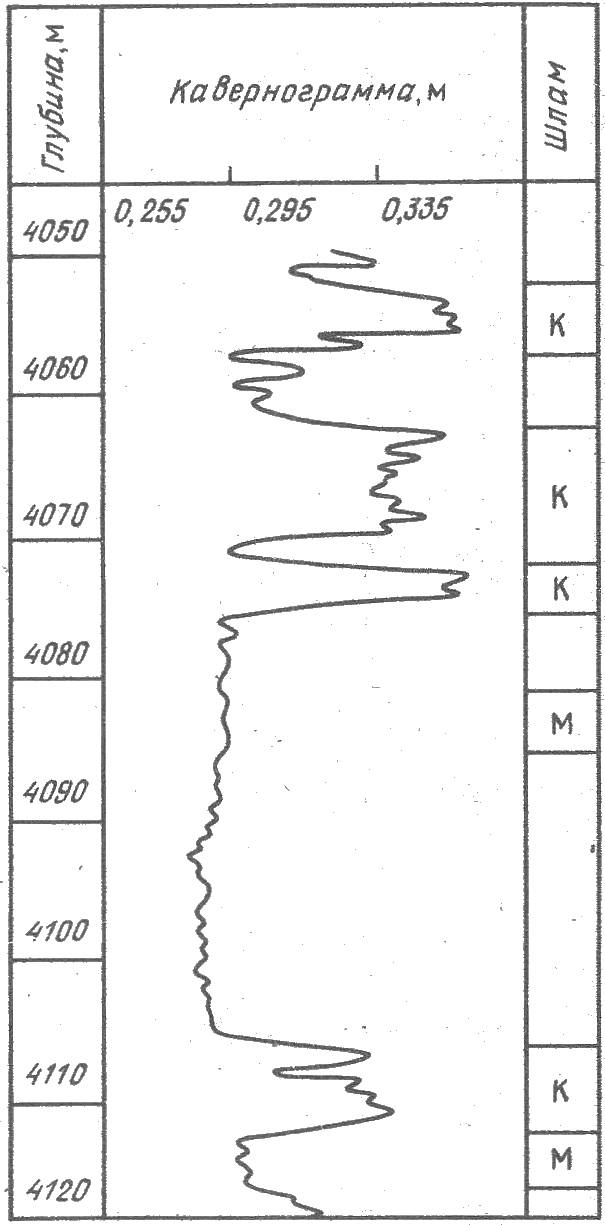
К - крупный, М - мелкий