
| К оглавлению журнала | |
|
УДК 553.98 |
cА.Г.Арье, В.С. Славкин, 1995 |
О МЕХАНИЗМЕ НЕФТЕГАЗОНАСЫЩЕНИЯ ПЕСЧАНЫХ ЛИНЗ В ГЛИНАХ
А.Г.Арье, В.С.Славкин
(ВНИГНИ)Конечная цель поискового этапа геолого-разведочных работ на углеводородное сырье состоит в обнаружении и оценке продуктивности природных ловушек нефти и газа. Как правило, она достигается путем проведения сейсморазведочных исследований с последующим разбуриванием выявленных структур. Очевидно, что возможность открытия залежи оказывается тем выше. чем с большей надежностью выполнена оценка вероятности заполнения ловушек углеводородными флюидами.
В некоторых случаях эта задача решается достаточно определенно в зависимости от структурно-геологических особенностей территории. Однако нередки ситуации, когда однозначное решение существенно затруднено. Особенно это актуально для локальных песчаных тел в глинистой толще.
Оставим за рамками анализа известные гипотезы о механизмах первичной миграции. Будем считать, что эти механизмы обусловливают выход углеводородного вещества из материнских глинистых пород в изолированный коллектор. Но такое предположение не снимает вопрос о том, каким образом и куда уходит замещаемая поровая жидкость,
Действительно, поскольку такое тело окружено со всех сторон непроницаемыми породами, в соответствии с традиционными представлениями подземной гидродинамики оно лишено возможности флюидообмена с вмещающими породами. Значит, поровый флюид не может выделиться из резервуара для высвобождения некоторого объема его порового пространства и последующего поступления в него соответствующего объема углеводородов, Другими словами, для образования залежи необходимо, чтобы седиментационные воды имели возможность выхода из резервуара. тогда как окружающие его глины, в силу выполнения ими роли покрышки, в соответствии с устоявшимися взглядами такую возможность полностью исключают,
Следовательно, в свете традиционных представлений суждение о присутствии в таких резервуарах нефти и газа должно быть однозначно отрицательным.
Тем не менее подобный вывод не всегда оправдан Например, в работе [3] показано, что по данным бурения клиноформные линзы песчаников, залегающие в толще непроницаемых глинисто-аргиллитовых пород неокома в пределах Приобского и Приразломного месторождений Западной Сибири, оказались насыщенными нефтью. При этом степень заполнения порового пространства резервуаров превышает 50 %. Значит, существенная часть воды. занимающая первоначально поровое пространство, мигрировала, несмотря на фильтрационное сопротивление глин.
В то же время для нефти это сопротивление оказалось непреодолимым и она сохранилась в коллекторе. Традиционные представления, опирающиеся на закон Дарси. не в состоянии дать удовлетворительное объяснение этому феномену.
Задача настоящей статьи - найти такое объяснение с помощью применения принципов нового направлений динамики подземных вод - геогидродинамики медленных потоков, разработке которого, хотя и в неявном виде, посвящались исследования Н.Н.Павловского (1922). П.А.Ребиндера (1940), Ф.А.Требина (1945), В.Энгельгардта и В.Тунна (1954) и многих других.
Работами этих исследователей показано, что применение закона Дарси в качестве базового для изучения региональной динамики подземных флюидов не всегда корректно вследствие чрезвычайно малых скоростей массопереноса. По их мнению, этот закон должен быть частным случаем более общего закона, справедливого для любых скоростей нетурбулентной фильтрации.
Региональные фильтрационные потоки характеризуются очень низкими скоростями, при которых отклонения от закона Дарси проявляются наиболее контрастно. Более того, если реальный градиент напора I = dP/dx, где Р - приведенное давление (напор), а x - расстояние, измеренное вдоль линии изменения напора, оказывается меньшим, чем величина начального градиента фильтрации Iо, процесс фильтрации в этом направлении прекращается. Такая ситуация в законе Дарси вообще не предусматривается, тогда как физически она вполне реальна.
Главная причина несовершенства закона Дарси состоит в том, что в нем не в полной мере учитывается взаимодействие жидкой и твердой фаз на границе поровая жидкость - минеральный скелет породы.
Между стенками перового канала и находящимися в нем молекулами жидкости существует физическое взаимодействие, ограничивающее подвижность молекул жидкости вплоть до того, что они образуют некоторую твердоподобную структуру, нечто похожее на жидкий кристалл. Однако прочность такой структуры падает по мере удаления от стенки порового канала к его центру. Поэтому при наличии некоторого градиента напора движение начинается в центральной части канала вследствие разрушения наименее прочного объема структуры. С увеличением градиента напора "живое сечение" потока возрастает. а с уменьшением - сокращается и обращается в нуль при достижении равенства I = Iо.
На основе этих идей в работе А.Г.Арье (1984) получено формульное выражение обобщенного закона фильтрации в виде
V=ko (l - Iо/I )2 * I (1)

Из формулы закона следует, что при
I ” Iо выражение (1) вырождается в закон Дарси V = kоI, а при I < Iо фильтрационное движение прекращается.Очевидно, что подход к проблеме заполнения углеводородами резервуара, изолированного в плане и разрезе глинами, не дает искомого решения и в случае использования с этой целью обобщенного закона фильтрации
(1). Дело в том, что вследствие низкой проницаемости глин значение начального градиента фильтрации для них обычно превышает единицы и даже десятки метров на 1 м. Значения же градиента напора природных флюидодинамических систем, как правило, не превосходят 0,01-0,10 м/м. И, поскольку в соответствии с уравнением (1) V = 0 при / < /о, фильтрационная изоляция такого резервуара обеспечена абсолютно.Справедливость изложенных соображений выдерживается лишь до той поры, пока процесс фильтрации рассматривается с позиции механики сплошной среды. Если же его проанализировать с точки зрения молекулярного строения жидкости. то проявляются особенности поведения ее отдельных молекул,
не фиксируемые математическим аппаратом Навье-Стокса. А именно, в каждом поровом объеме имеется как минимум одна точка, в которой равнодействующая поверхностных сил равна нулю. Совокупность таких точек в поровом канале образует некоторую линию. При I<=Iо весь объем порового пространства заполнен неподвижной желeподобной жидкостью. однако всякая молекула такой жидкости находится в броуновском движении и в момент пересечения указанной линии перестает испытывать на себе влияние поверхностных сил стенок канала. Вследствие этого она вынуждена отклоняться с наибольшей вероятностью в направлении снижения напора.По определению формула
(1) справедлива только до градиента / = /о, при достижении которого процесс фильтрации прекращается. Необходимо подчеркнуть, что под фильтрацией подразумевается только такое движение жидкости в поровом канале, когда в нем принимает участие число молекул, достаточное, чтобы сформировать эпюру скоростей, описываемую уравнением Стокса-Пуазейля.Однако, как было замечено, массоперенос не прекращается и при
/ < /о. Молекулы жидкости в результате тепловых флуктуации пересекают ось порового канала. Это вынуждает их дрейфовать в сторону меньшего значения напора. Движение в таком режиме названо файлюацией для того. чтобы отличить его от движения в режиме фильтрации. Массовая скорость файлюации связана с градиентом напора выражениемv=l I при I < Iо, (2)
где
v - скорость массопереноса;l
- коэффициент файлюации (Арье А.Г„ 1984).В той же работе А.Г Арье показано, что

Важно, что коэффициент файлюации в явном виде зависит от температуры жидкости и индивидуальной подвижности ее молекул, выраженной периодом трансляции. В этом заключается его принципиальное отличие от коэффициента фильтрации, зависящего, как известно, только от кооперативной подвижности молекулярной массы, выражаемой коэффициентом вязкости
* в соответствии с соотношением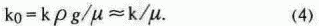
Основываясь на указанном отличии коэффициентов файлюации и фильтрации, по аналогии с
(4) выражение (3) можно представить а виде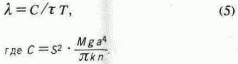
Как видно из формулы
(5), коэффициент файлюации обратно пропорционален периоду трансляции молекул жидкости и ее абсолютной температуре, а формула (4) показывает, что коэффициент фильтрации обратно пропорционален вязкости молекулярной массы.Если нормировать коэффициенты фильтрации Кт и файлюации
lT , по их значениям при какой-то выбранной температуре То, то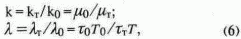

Формулы
(2) и f3) получены исходя из теоретических представлений о процессе фильтрации и .поэтому требуют экспериментальной проверки.В качестве такой проверки использованы результаты уникальных экспериментов по изучению фильтрации через специально приготовленное тонкопористое стекло
[I]. В пластинке стекла толщиной 2*10-4 м были сделаны цилиндрические круглые отверстия диаметром 20*10-10 м. Затем через них при перепаде давления от долей мегапаскаля до 10 МПа (градиент напора 5*104- 5*106 м/м) просачивалась дистиллированная вода при разных температурах. Исследовалась зависимость объемной скорости жидкости от градиента напора в изотермических условиях при температурах 293 К (20 °С), 313 К (40 °С), 333 К (60 °С) и 343 К (70 °С), Такая зависимость изучалась на каждой ступени изменения температур.Результаты экспериментов показали, что на каждой из выбранных ступеней зависимость скорости от градиента напора носит прямолинейный характер, причем все прямые исходят из нулевой точки графика в координатах скорость
- градиент напора. Уклон их возрастает с ростом температуры. Отсюда в работе [1] сделан вывод о том, что закон Дарси выполняется при любых скоростях нетурбулентной фильтрации, а начальный градиент фильтрации (как минимальное значение градиента напора, при котором прекращается физический массоперенос в пористой среде) отсутствует **.Однако авторы эксперимента обратили внимание на то обстоятельство, что с увеличением температуры от
20 до 70 °С скорость массопереноса возрастает несколько быстрее, чем уменьшается вязкость флюида (расхождение расчета с экспериментом составляет 10-25 %), Необходимо напомнить, что если реализуется процесс фильтрации, то скорость в соответствии с уравнением (4) должна возрастать так же, как снижается вязкость, т.е. отмеченного расхождения быть не должно. Но поскольку оно имеется, авторы работы [1] предположили, что с повышением температуры от 20 до 70 °С увеличивается пропускная способность поровых каналов, т.е. проницаемость пористой среды. Относительная величина такого изменения по результатам проведенных экспериментов максимально достигает 25 %. Увеличение "живого сечения" поровых каналов происходит за счет того. что при нагревании часть слоя молекул воды, удерживаемого стенкой канала, "плавится" и переходит в поток, что вызывает изменений проницаемости среды.Такая точка зрения представляется недостаточно обоснованной по следующим соображениям.
1. Вследствие особенностей технологии изготовления анализируемая пористая среда представлена цилиндрическими прямыми каналами. Поэтому "плавление" связанного флюида может приводить к вовлечению в поток как минимум одного мономолекупярного слоя, толщина которого составляет ~ 3-10-10 м. Максимальное число таких слоев в цилиндрическом канале радиусом 10 •10-10 м не может быть более трех. При этом важно помнить, что при температуре 20 °С течение в каналах наблюдалось, следовательно, стенка канала могла удерживать не более двух мономолекулярных слоев. Если это так, то непонятно, за счет чего могло увеличиваться "живое сечение" канала при переходе на третью температурную ступень 70 °С, поскольку возможности роста проницаемости были исчерпаны на первых двух ступенях 40 и 60 °С.
2. Если бы механизм, предполагаемый авторами эксперимента, реализовался, проницаемость менялась бы минимум в 2-3 раза, тогда как на самом деле это изменение не превышало 25 %.
По-видимому, дело здесь в другом. В работе А.Г.Арье
(l984) получена формула, позволяющая определить для прямолинейных цилиндрических каналов круглого сечения величину начального градиента фильтрации как градиента, характеризующего вырождение фильтрационного потока в файлюационный. Применение ее к рассматриваемому случаю, абсолютно адекватному условиям вывода формулы, показывает, что начальный градиент фильтрации воды для поровых каналов радиуса 10-9 м составляет 109 - 1011. Данный же эксперимент проводился при градиентах напора не выше 5106, т.е. существенно меньших, чем начальный градиент фильтрации. Но тогда по определению файлюации должна выполняться зависимость (2), что, как будет показано, и имеет место в эксперименте. Поэтому справедливо предположить, что колебание температурного режима опыта закономерно должно приводить к изменению коэффициента файлюации за счет вариаций периода трансляции и температуры жидкости. Значения вариаций периодов трансляций молекулы воды под действием температуры измерены с высокой точностью [4]. Если подставить их в формулы (6). то не составляет труда спрогнозировать по выражению (2) относительное изменение скорости массоперенаса в результате изменений температуры. Такой расчет был выполнен, результаты его сопоставления с данными эксперимента и предполагаемым изменением скоростей фильтрации и файлюации приводятся в таблице.Из
таблицы видно, что расчет относительной скорости, реализованный в соответствии с предположением о файпюационном характере движения. дает более близкие к экспериментальным результаты. Максимальное расхождение не выходит за пределы 1.5 %. тогда как предположение о фильтрационном механизме приводит к ошибке расчета более 25 %. На этом основании предпосылка о файлюационном массопереносе представляется доказанной,Необходима отметить, что В.И.Порядин
[2] независимо от авторов настоящей статьи получил формулы скорости файлюации и коэффициента файлюации, совпадающие с аналогичными, обоснованными еще в 1982 г. А.Г.Арье В работе [2] наличие явления подтверждается теоретически,На основании изложенного можно считать файлюацию третьим, ранее неизвестным режимом гравитационного движения подземных флюидов. отличающимся от ламинарного и турбулентного тем, что в его реализации участвует малое число молекул, вследствие чего интенсивность массопереноса в таком режиме контролируется не кооперативными свойствами молекулярной массы, а индивидуальными характеристиками отдельных молекул. В этом режиме, как правило, происходит движение подземных вод глубоких частей артезианского бассейна, а также поровых вод в глинах и других малопроницаемых породах при отсутствии в них очагов интенсивного пьезометрического возмущения.
В свете представлений о процессе файлюации затруднения при решении поставленной в начале статьи задачи с очевидностью отпадают.
Действительно, глины, обладающие обычно весьма высокими начальными градиентами фильтрации, полностью экранируют фильтрационный массоперенос. Однако файлюационный обмен с окружающей средой при этом не прекращается. Более того, формула
(3) показывает, что чем больше удельная поверхность глины, т.е. чем более она дисперсна и, следовательно, менее проницаема для фильтрации, тем выше ее файлюационная проницаемость. Но файлюация - свойство однородного флюида. Наличие фазового раздела прекращает процесс для одной из фаз. Если какая-либо из них образует молекулярный континум в объеме другой, то она может передвигаться в последней только кооперативно. В противном случае она не может называться фазой по определению. Нефть (или газ) и поровая вода образуют между собой фазовую границу, т.е. углеводородное вещество в воде может двигаться только континуально. Однако водой заполнено и поровое пространство глин, которые составляют непреодолимое препятствие для фильтрации, т.е. континуального течения. Следовательно, через покрышку проникает только вода, причем отдельными молекулами путем файлюационного просачивания.Важно отметить, что участки глин, контактирующие с углеводородным флюидом, непроницаемы для молекул воды, даже в режиме файлюации.
Все изложенное позволяет обосновать выделение полностью изолированных нефтегазонасыщенных линз коллекторов как самостоятельных и весьма своеобразных с точки зрения разведки и эксплуатации объектов. Разумеется, такого рода объекты и ранее
встречались в практике поисково-разведочных работ. Однако в силу неясности механизма их генезиса они нередко искусственно приводились к "нормальному" виду, т.е. путем некоторых натяжек в корреляции разреза эти объекты относили к виду пластовых залежей и им приписывалась прямая гидравлическая связь с общей флюидодинамической системой бассейна. Отсюда вытекают, по крайней мере, два весьма отрицательных следствия.Во-первых, их разведка нередко затягивалась и сопровождалась большими и нецелесообразными затратами на обнаружение водонефтяной зоны и обоснование отметки "водонефтяного контакта" там, где его и не может быть.
Во-вторых, необоснованное объединение изолированных нефтегазонасыщенных линз с общей флюидодинамической системой приводит к выбору принципиально неверных схем разработки. Ошибки еозникали вследствие попыток некорректной организации заводнения таких залежей.
Понятно, что "законтурное" заводнение в принципе не может оказать какого-либо влияния на изолированный продуктивный пласт. Реальным средством поддержания пластового давления в таких условиях является только закачка воды в тело залежи.
Рекомендуется при построении окончательных моделей геологического строения залежей рассматривать (в сложных случаях
) как равноправный вариант существования гидродинамически изолированных нефтегазонасыщенных линз.*Вязкость
и подвижность молекул, отражая одно и то же свойство жидкости, не аддитивны по отношению друг к другу.**Прямолинейнан связь между скоростью фильтрации и градиентом напора свидетельствует о постоянстве значения множителя перед I в формуле (1) и его зависимости от m, как это показано в формуле (4).
ЛИТЕРАТУРА
1.
Дерягин Б.В., Чураев Н.В., Муллер В.М. Поверхностные силы. - М.~. Наука, 1985.2.
Порядки В.И. Термодинамические и молекулярно-кинетические аспекты формирования порового пространства осадочных пород. - Алма-Ата, 1986. - Деп. в ВИНИТИ, № 5465-В.3
Сейсмолитологические модели неокомских клиноформ Приобско-Салымской зоны/ В.С.Славкин, Н.С.Шик, А.А.Гусейнов и др. // Геология, геофизика и разработка нефтяных месторождений. - 1994. - № 5-6. - С. 47-52.4.
Эйзенберг Д., Кауцман В. Структура и свойства воды. - М.: Гидрометеоиздат, 1975.
|
Расчетные данные |
|||||
|
фильтрация |
файлюация |
||||
|
Т, К |
W, % |
m, 10-3 Па -с |
V, % |
t , 10-12с |
v,% |
|
293 |
100 |
1,00 |
100 |
10,00 |
100 |
|
313 |
167 |
0,65 |
154 |
5,94 |
168 |
|
333 |
244 |
0,47 |
213 |
4,04 |
247 |
|
343 |
305 |
0,41 |
244 |
3.30 |
303 |
Примечание.
W — Wt/W20 - относительная скорость течения воды в эксперименте (отнормированная по скорости при 20 °С); V = Vt/V20 и v - vt/v20 - соответственно относительная скорость фильтрации и файлюации.