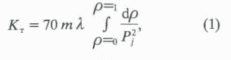
|
УДК 553.98.061.4 |
© И.В.Шершуков, 1995 |
НОВЫЙ МЕТОДИЧЕСКИЙ ПОДХОД К ОЦЕНКЕ ТЕОРЕТИЧЕСКОЙ ПРОНИЦАЕМОСТИ ПО ПОРОМЕТРИЧЕСКОЙ КРИВОЙ
И.В. Шершуков (ГАНГ им. И.М.Губкина)
При исследовании пустотного пространства коллекторов нефтегазоносных карбонатных пород применяются различные методы. Принципиальная основа выбора комплекса методов определяется подразделением карбонатных коллекторов на поровый и трещинный типы. Существенные отличия в содержании и характере распределения остаточной воды в порах и трещинах, а также несоразмерность этих типов пустот обусловливают специфику методического подхода к оценке порового и трещинного типов коллекторов. Сложный тип коллектора характеризуется различным долевым участием пор, каверн и трещин в строении пустотного пространства карбонатных пород. Методика изучения и оценки выбирается в зависимости от преобладающей роли тех или иных видов пустот в создании емкостных свойств и фильтрации.
Поровый тип коллектора надежно оценивается рядом параметров (пористость, проницаемость, остаточная водонасыщенность и др.), связанных тесными корреляционными зависимостями [1].
Изучение карбонатных пород по большим образцам кубической формы (с гранью 5 см) позволяет оценить тип коллектора по существенно различному характеру изменения ориентированной проницаемости. Анизотропия проницаемости в трех взаимно перпендикулярных направлениях, свидетельствующая об усложнении структуры порового пространства за счет развития каверн или трещин, свойственна сложным типам коллекторов.
Поровый тип коллектора, как правило, характеризуется изотропностью фильтрационных свойств. Критерием оценки типа коллекторов является геометрия порового пространства, определяющая фильтрационные свойства пород и количество остаточных флюидов.
Наиболее полную информацию дает метод вдавливания ртути в образец при различных давлениях. Особенности структуры порового пространства, а именно:
размеры поперечного сечения, извилистость и форма каналов, распределение их в поровом объеме, степень сообщаемости между собой – предопределяют фильтрационные свойства пористых сред.Исследованиями, проведенными во ВНИГНИ, выявлено значительное расхождение между величинами проницаемости, теоретически рассчитанной по формуле Пурцелла при обработке ртутной порометрической кривой и экспериментально измеренной на образцах большого размера. Наибольшие отклонения отмечены для коллекторов порового типа с проницаемостью от 0,001 до 0,5 мкм
2 , при этом расчетная проницаемость значительно превышает экспериментальную.Расчет фильтрационной способности пористой среды при обработке данных ртутной порометрии, как правило, проводится способом Пурцелла на основе модели с прямолинейными протяженными капиллярными трубками различного сечения. Однако пористые среды в карбонатных породах отличаются более сложным строением и характеризуются сочетанием длинных и коротких по протяженности поровых каналов, а также значительной изменчивостью их поперечного сечения. За счет этого в реальных средах нарушается связанность некоторой части поровых каналов наиболее крупных размеров, в результате чего они сообщаются только через мелкие поры.
Обработка большого числа порометрических кривых по формуле Пурцелла позволила получить кривую распределения фильтрующих пор, из которой видно, что для обеспечения экспериментально измеренной величины фильтрации через эти породы было бы достаточно незначительного числа пор крупного размера (
рис. 1). Распределение всей совокупности пор по размерам показано на гистограммах; кумулятивная кривая позволяет оценить неоднородность структуры и средний радиус пор; на графике отражены диапазон фильтрующих пор и долевое участие их в фильтрации.Сравнение величин теоретической и экспериментальной проницаемостей доказывает несостоятельность вывода о существенном вкладе самых крупных пор в фильтрацию (
рис. 2). Полученное расхождение объясняется большей сложностью геометрии порового пространства карбонатных пород и неучетом степени связанности пор между собой.С целью получения более достоверных значений теоретической проницаемости автором в 1986 г. был разработан новый методический прием математической обработки результатов ртутной порометрии, позволяющий учитывать извилистость и сообщаемость поровых каналов при расчете фильтрации. Как отмечалось, поровые каналы реальных сред существенно отличаются от модели Пурцелла. В пористых карбонатных средах поровые каналы различных радиусов сообщаются друг с другом и образуют сложную систему проводящих элементов. Фильтрационная способность системы трубок определяется "пропускной" способностью наименьшего по размерам элемента. Более крупные элементы в этой системе, составляя малую часть ее объема, не могут сформировать свою самостоятельно связанную и протяженную систему, т
.е. оказываются не способны обеспечить фильтрацию.Модель строения перового пространства, предложенная автором [4,5], более точно соответствует реальным пористым средам и представляет собой набор пересекающихся капиллярных трубок переменного сечения. Существенное отличие предложенной модели от использованной Пурцеллом заключается в необходимости учитывать связанность проводящих элементов. Для этого следует рассматривать извилистые капилляры переменного сечения как ряд прямолинейных отрезков, соединенных друг с другом.
На необходимость введения поправок за извилистость указывалось и ранее (Бурдайн Н.Т. и др., 1950; Амикс Дж. и др., 1962), но работ по достоверному учету этого параметра не было. В.
Энгельгард (1964) отмечал, что для полного описания геометрической структуры перового пространства надо определить пористость, проницаемость, удельную поверхность твердого вещества, функцию распределения пор и извилистость.В формулу Пурцелла для расчета теоретической проницаемости входит литологический коэффициент
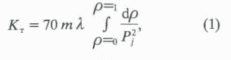
где
m - пористость, %; r доля объема капилляров, заполненных ртутью при давлении Pj; l - литологический коэффициент.Для карбонатных пород значение
l принято равным 0,071. Этот коэффициент соответствует более сложной, чем пучок прямолинейных капиллярных трубок, конфигурации порового пространства. Однако сложность геометрической структуры порового пространства литологическим коэффициентом полностью не учитывается. Система проводящих элементов образует "кластер", т.е. является связанной, если выполняется условиеnl3 > Рс , (2)
где
n - концентрация или число капиллярных трубок данного радиуса в единице объема (например, в 1 см3); l - длина капиллярной трубки, см; Рс - некоторое число, которое называется пороговым значением. Пороговое значение Рс зависит от пространственной организации проводящих элементов. При данных расчетах использовано пороговое значение 0,25, характеризующее расположение проводящих элементов в трех взаимно перпендикулярных направлениях. Таким образом, граничное значение длины элементов lс определяется из условияnlc3 = 0,25. (3)
С точки зрения связанности пор значение
lс характеризует относительно прямолинейный отрезок извилистого капилляра, на конце которого в результате перегиба происходит как бы переход к другому капилляру длиной lc.Длина поровых капилляров в карбонатных породах превышает их диаметр в 2-6 раз, что было установлено автором данной статьи при использовании метода электронной микроскопии в режиме
катодной люминесценции [2,3]. Для поровых каналов с радиусом 10-32 мкм длина не более 100 мкм; для крупных пор радиусом 40-50 мкм она составляет 100-150 мкм, реже до 300 мкм. Для ртутного поромера "Поромер-70Н" значения радиусов пор 50 мкм являются максимальными, поэтому для учета связанности поровых капилляров выбрано критическое значение lс = 100 мкм.Для расчета условия связанности поровых каналов по данным метода ртутной порометрии автором настоящей статьи выведены следующие формулы.
Объем пор данного радиуса в единице объема (1 см3 )
Vi=m*mi/100 <4>
где
m - пористость, %; mi - насыщенность или содержание пор, %, данного радиуса Ri, см.Суммарная длина всех капиллярных трубок данного радиуса в 1 см
3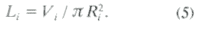
Для трубок критической длины концентрация в 1 см
n = Li/lc. (6)
Тогда согласно формулам (3)-(6) определим критические значения длины капилляров
lс при данной их концентрации, необходимые для образования "кластера" в объеме 1 см3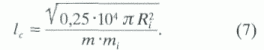
Для системы, состоящей из капиллярных трубок различных радиусов
Ri при насыщенности mi, используя выбранное значение 1С= 100 мкм, с учетом формул (2), (7) получаем условие связанности:
Результаты расчетов по предложенным формулам свидетельствуют, что в сложных пористо-кавернозных средах поры крупного размера не образуют самостоятельно связанной системы, если в 1 см
3 породы их суммарная длина составляет менее 2500 см. Например, связанность системы пор радиуса R1 будет достигаться при включении в нее пор меньшего радиуса R2, величина которых и определит значение фильтрации.При расчете проницаемости необходимо принимать во внимание, что за счет крупных пор радиуса
R1 увеличивается число пор в системе, образованной более мелкими порами радиуса R2.Если
L1 и L2 – суммарные длины пор соответственно радиусов R1 и R2, то увеличенное значение насыщенности (т2*), подставляемое в формулу Пурцелла (1), составит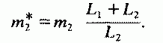
Аналогично, если связанность достигается позднее, лишь при включении в систему пор радиуса
Ra, значение насыщенности mа рассчитывается по формуле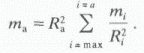
Применение указанного подхода к учету связанности пор при расчете проницаемости по данным ртутной порометрии позволило оценить истинный диапазон пор, обеспечивающих фильтрацию флюидов в этой системе, и определить величину среднего радиуса фильтрующих пор (
рис. 3). Сопоставление значений теоретической проницаемости с учетом связанности с данными экспериментальных измерений на образцах большого размера выявило хорошую сходимость (рис. 4). Корреляционная зависимость между параметрами возросла, стала более тесной, что выразилось в оценке коэффициента корреляции (0,96). В случае установленного распределения поровых капиллярных трубок разных радиусов по длинам (при их предельной протяженности) условие связанности по аналогии с выводом формулы (8) можно записать в виде: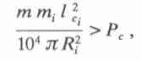
где
lСi - предельная длина капиллярных трубок данного радиуса Ri. Новый методический подход к оценке фильтрационных свойств пористых сред наглядно демонстрирует необходимость учета связанности проводящих элементов порового пространства в единую систему. Количественными показателями особенностей геометрии порового пространства являются: средний радиус всей совокупности пор, отражающий неоднородность строения порового пространства; диапазон радиусов пор, развитых в породе и определяющих фильтрацию, долевое участие пор различного радиуса в фильтрации и средний радиус фильтрующих пор (таблица). Проведенная интерпретация порометрических кривых позволяет выделить две подсистемы в структуре порового пространства: емкостную и фильтрационную.ЛИТЕРАТУРА
Criterion to estimate resevoirs' type and classes is considered to be the pore space geometry controlling filtration properties of rocks and quantity of residual fluids. When processing mercury poromet-ric data, calculation of filterability in pore media is generally performed using Purtzell method based on the model with extensive rectilinear capillary tubes of variable section. However, pore media in carbonate rocks are distinguished by more complex structure and characterized by combination of long and short pore channels and to a great extent by their cross section's changeability, resulted in disturbance in real media of coherence for some part of pore channels having the most large sizes. The model of pore space structure proposed by the author more exactly complies with real pore media and represents a set of intersecting capillary tubes of variable section. The significant difference of proposed model as compared with the model used by Purtzell consists in the necessity to account the conductive elements coherence. For this purpose the sinuous capillaries of variable section should be regarded as a set of rectilinear segments connected with each other. The author inferred a set of formulas to calculate conditions of pore channels coherence based on the mercury poro-metry data. New methodical approach to evaluate filtration properties of pore media witnesses that account of conductive elements coherency into a single system within the pore space is of great importance. The quantitative indicators of the pore space geometry are the following: medium width of all the sum total of pores reflecting the porous space structure heterogeneity; a spectrum of pore widths developed in rock and controlling filtration, various pore width sharing in filtration and medium width of filtrating pores. The proper interpretation of porometric curves allows to distinguish two subsystems within the pore space structure, i.e. porosity and permeability.
Структурные характеристики карбонатных пород, полученные на различных моделях (нефтегазоконденсатное месторождение Жанажол,
KT-I, скв.19)|
Глубина, м |
Пористость, % |
Экспериментальная газопроницаемость, n· 10 мкм2 |
Остаточная вода, % |
Содержание пор с радиусом менее 0,1 мкм, % |
Средний радиус пор, мкм |
Модель без учета связанности пор |
Модель с учетом связанности пор |
|||||||||
|
I |
II |
III |
эффективная |
Поры, определяющие фильтрацию |
Теоретическая проницаемость, n·10-3 мкм2 |
Поры, определяющие фильтрацию |
Теоретическая проницаемость, n·10-3мкм2 |
|||||||||
|
диапазон радиусов, мкм |
средний радиус, мкм |
содержание, % |
диапазон радиусов, мкм |
средний радиус, мкм |
содержание, % |
|||||||||||
|
2572-2575 |
18,6 |
15,1 |
22,8 |
23,6 |
11,6 |
21,6 |
- |
2,5 |
5-16 |
6,7 |
30,0 |
48,2 |
3,75-16,0 |
6,7 |
43,0 |
39,0 |
|
2577-2585 |
13,1 |
4,5 |
9,5 |
8,8 |
7,8 |
19,0 |
8,0 |
1,25 |
5-16 |
8,0 |
28,0 |
38,3 |
3,75-16,0 |
6,7 |
37,0 |
27,9 |
|
2577-2585 |
13,1 |
4,5 |
9,5 |
8,8 |
7,8 |
19,0 |
11,3 |
2,0 |
10-32 |
16,0 |
24,0 |
133,4 |
6,7-32,0 |
12,5 |
33,0 |
43,4 |
|
2593-2601 |
24,0 |
313,8 |
385,2 |
262,5 |
366,5 |
13,1 |
- |
10,0 |
12,5-32,0 |
20,0 |
44,0 |
602,4 |
10-32 |
16 |
52,0 |
352,5 |
|
2601-2610 |
21,8 |
154,2 |
157,2 |
141,4 |
124,0 |
16,7 |
10,0 |
5,0 |
10-50 |
16,0 |
28,0 |
302,2 |
6,8-50,0 |
12,5 |
41,0 |
165,0 |
|
2601-2610 |
22,6 |
95,2 |
103,9 |
127,0 |
101,9 |
16,6 |
4,0 |
3,75 |
8-25 |
12,5 |
36,0 |
223,5 |
6,7-25,0 |
12,5 |
42,0 |
144,0 |
|
2615-2622 |
14,8 |
0,9 |
3,95 |
1,0 |
Не опр. |
30,9 |
13,0 |
0,375 |
0,75-6,7 |
1,0 |
24,0 |
2,1 |
0,75-6,7 |
1,0 |
24,0 |
1,7 |
|
2615-2622 |
18,7 |
3,7 |
Не опр. |
602,6 |
Не опр. |
Не опр. |
8,0 |
5,0 |
6,7-25,0 |
10,0 |
43,0 |
154,2 |
6,7-25,0 |
10,0 |
43,0 |
83,3 |
|
2615-2622 |
13,6 |
49,5 |
60,4 |
44,5 |
49,9 |
18,9 |
10,0 |
2,5 |
6,7-25,0 |
10,0 |
30,0 |
73,2 |
5-25 |
8,0 |
38,0 |
33,6 |
|
2615-2622 |
13,3 |
64,7 |
63,1 |
83,8 |
62,6 |
19,6 |
13,3 |
5,0 |
16-50 |
25,0 |
27,5 |
404,5 |
8-50 |
20,0 |
44,4 |
85,2 |
|
2667-2675 |
14,5 |
0,44 |
0,67 |
0,53 |
0,21 |
24,2 |
5,0 |
10,0 |
12,5-50,0 |
20,0 |
47,5 |
195,2 |
8-50 |
16,0 |
63,0 |
50,4 |
|
2675-2682 |
14,8 |
2,9 |
5,0 |
6,0 |
0,9 |
19,6 |
9,2 |
1,5 |
1,5-5,0 |
2,0 |
60,3 |
5,4 |
1,5-5,0 |
2,0 |
60,3 |
5,2 |
|
2691-2694 |
20,9 |
293,1 |
303,5 |
Не опр. |
Не опр. |
15,3 |
5,6 |
8,0 |
10-50 |
16,0 |
41,6 |
420,2 |
8-50 |
12,5 |
50,0 |
237,0 |
|
2691-2694 |
17,8 |
3,98 |
9,3 |
27,0 |
- |
30,4 |
6,0 |
3,75 |
3,75-10,0 |
5,0 |
52,0 |
43,4 |
3,75-10,0 |
5,0 |
52,0 |
43,4 |
|
2738-2743 |
10,9 |
2,5 |
2,3 |
2,6 |
- |
30,2 |
18,9 |
0,75 |
2,0-12,5 |
2,5 |
30,4 |
7,1 |
1,5-12,5 |
2,5 |
39,6 |
4,5 |
|
2787-2794 |
4,3 |
1,6 |
9,5 |
0,001 |
- |
Не опр. |
63,0 |
0,05 |
1,25-3,75 |
2,0 |
14,0 |
0,42 |
1,0-3,76 |
1,5 |
17,0 |
0,3 |
Рис.1. КРИВЫЕ РАСПРЕДЕЛЕНИЯ ПОР ПО ВЕЛИЧИНЕ РАДИУСОВ И ИХ УЧАСТИЕ В ФИЛЬТРАЦИИ (МЕСТОРОЖДЕНИЕ ТЕНГИЗ)
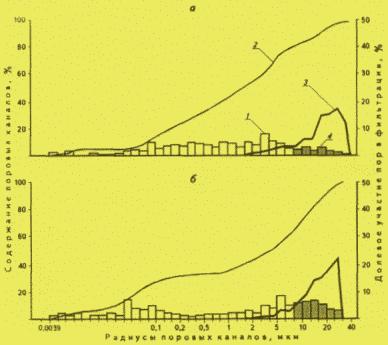
а - образец 5885, скв. 7, интервал 4015-4021 м, известняк реликтово-оолитовый; К = 0,013 мкм
2; Кт - 0,057 мкм2; m = 14,0 %; г = 1 мкм; rф = 20 мкм, где К, Кт - экспериментальная и теоретическая газопроницаемость; т - открытая пористость; r - средний радиус всей совокупности пор; гф - средний радиус фильтрующих пор;б - образец 6128, скв. 44, интервал 4141-4148 м, известняк водорослевый; К - 0,051 мкм
2; Кт - 0,120 мкм2; m = 15,6 %; r = 2; rф = 25;1 - гистограмма распределения всей совокупности пор по величине радиусов; 2 - кумулятивная кривая; 3 - долевое участие пор в фильтрации; 4 - величина радиусов пор, участвующих в фильтрации
Рис.2. СООТНОШЕНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ И ТЕОРЕТИЧЕСКОЙ (БЕЗ УЧЕТА СВЯЗАННОСТИ ПОР) ПРОНИЦАЕМОСТИ
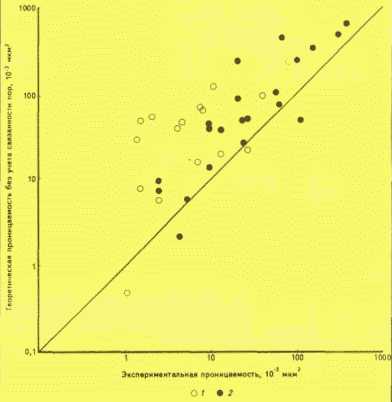
Месторождения:1 - Карачаганак, 2 - Жанажол
Рис.3. ИЗМЕНЕНИЕ ДОЛЕВОГО УЧАСТИЯ ПОРОВЫХ КАНАЛОВ В ФИЛЬТРАЦИИ ПРИ УЧЕТЕ СВЯЗАННОСТИ ПОР В СИСТЕМУ (МЕСТОРОЖДЕНИЕ ТЕНГИЗ)
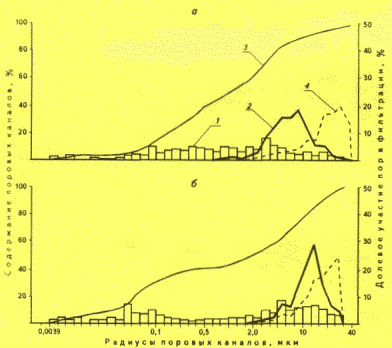
а - образец 5885, Ктс = 0,013 мкм ,
rф - 6,7 мкм, где Ктс - теоретическая проницаемость с учетом связанности пор в систему, б - образец 6128; Ктс - 0,058 мкм2, rф = 12,5 мкм; остальные параметры см. на рис. 1; 1 - содержание пор данного размера, %; 2 - кривая долевого участия пор в фильтрации с учетом связанности пор; 3 - кумулятивная кривая; 4 - кривая долевого участия пор в фильтрации по ПурцеллуРис.4. СООТНОШЕНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ И ТЕОРЕТИЧЕСКОЙ (С УЧЕТОМ СВЯЗАННОСТИ ПОР) ПРОНИЦАЕМОСТИ
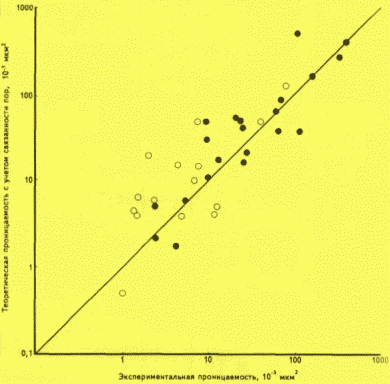
Усл. обозначения см. на рис. 2