К оглавлению	УДК 550.834:553.98.061.4
	© Е.А. Копилевич, 1995

ИЗМЕНЕНИЕ СКОРОСТИ РАСПРОСТРАНЕНИЯ ПРОДОЛЬНЫХ ВОЛН В СВЯЗИ С ЕМКОСТНЫМИ СВОЙСТВАМИ КОЛЛЕКТОРОВ

Е.А. Копилевич (ВНИГНИ)

Известно, что скорость распространения продольных волн в коллекторах постоянного или слабо меняющегося минерального состава зависит в основном от пористости. Это нашло свое отображение при методе отраженных волн в виде зависимости, показанной Н.Н. Пузыревым (1959), а при определении пористости по данным акустического каротажа (АК) - в форме широко применяющегося уравнения среднего времени [3.

Однако при практическом изучении емкостных свойств нефтегазовых коллекторов сталкиваются не со сплошными однородными коллекторами, а с продуктивной толщей, состоящей из i коллекторов, характеризующихся способностью принимать и отдавать флюид и имеющих пористость m_ki выше определенного порога и эффективную толщину hэф_i., а также j неколлекторов, не способных принимать и отдавать флюид с пористостью m_нкj, меньшей заданного порога по сравнению с m_k (m_HK < m_K). В таком случае суммарная эффективная толщина коллекторов будет равна

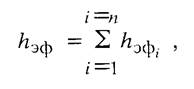
а суммарная толщина неколлекторов определяется разностью (Н - hэф), где Н - толщина всей продуктивной толщи, которую примем постоянной, поскольку на практике Н если и меняется, то в значительно меньшей степени, чем hэф. Как и в случае с коллекторами, условимся о постоянстве минерального состава продуктивных отложений, поскольку в реальной геологической среде это или песчаники, или карбонаты (известняки, доломиты), т.е. породы в минералогическом плане более или менее однородные.

Такая постановка задачи правомерна с геологических позиций и к тому же соответствует разрешающей способности среднечастотной (< 90 Гц) сейсморазведки, поскольку отдельные тонкие пласты коллекторов не могут быть изучены, тогда как продуктивная толща, состоящая из коллекторов и неколлекторов, при Н > 15 м доступна для разнообразной се характеристики сейсмическим методом.

Величина средней пористости такой продуктивной толщи, определяемая на качественном, а иногда и количественном уровне по данным сейсморазведки в межскважинном пространстве [2], хотя и характеризует емкостные свойства изучаемых отложений, однако не может быть использована для установления объема залежи и подсчета запасов УВ. Для этого необходимо знать пористость коллекторов m_k и их эффективную толщину hэф.

В работе [4] впервые предложен и реализован универсальный принцип наилучшего отображения в вариациях сейсмических параметров продольных отраженных волн, характеризующих продуктивную толщу изменения емкостных свойств коллекторов в виде параметра их эффективной удельной емкости q, представляющего собой произведение пористости коллекторов mk на эффективную толщину hэф -

q = mk* hэф.

На основе выявленной зависимости акустических (Δt_AK, ΔV_AК) и псевдоакустических (Δt_ПАK, ΔV_ПАК) параметров, характеризующих продуктивную толщу карбонатов башкирского яруса среднего карбона Астраханского газоконденсатного месторождения, от q(Δt_ПАK, ΔV_ПАК) = f(q) впервые построена карта q с количественным определением этого параметра в межскважинном пространстве по данным сейсморазведки [4].

Подобные зависимости были установлены затем в существенно иных сейсмогеологических условиях: в пределах Соль-Илецкого выступа, Тимано-Печорской НГП, на Каймысовском (Западная Сибирь) и Камовском (Восточная Сибирь) сводах, в Туркменистане. Имеются многочисленные подтверждения правильности определения q при последующем бурении (83 скважины) в пределах прогнозируемой точности (~ 2-20 %).

На основании большого объема сейсмического моделирования различных сейсмогеологических объектов США, Мексики и Ближнего Востока сделан вывод и показано, что ни пористость, ни эффективная толщина не определяются достаточно устойчиво по значениям сейсмических амплитуд, но произведение пористости на эффективную толщину (эффективная удельная емкость коллекторов) хорошо коррелируется с сейсмической амплитудой для всех изученных многочисленных типов разреза. Этот результат, полученный независимым путем на других территориях, подчеркивает универсальность избранного подхода.

Теоретические аспекты обоснованности и необходимости использования произведения q = mk*hэф как универсального фактора, главным образом определяющего изменение скорости распространения продольных волн в продуктивных карбонатных и терригенных отложениях, до сих пор не рассмотрены, что, конечно, сдерживает дальнейшее развитие и внедрение разработанных во ВНИГНИ методики и технологии определения емкостных свойств коллекторов в межскважинном пространстве по данным сейсморазведки МОГТ (Е.А. Копилевич, В.С. Славкин и др., 1988; 1989; 1993; 1994).

Задача настоящей статьи состоит в попытке восполнить этот пробел и обосновать полученный экспериментальный феномен с позиций современной теории распространения продольных сейсмических волн.

Для однородной абсолютно упругой изотропной среды известно уравнение, связывающее скорость распространения продольных волн V_p с модулем Юнга Е, коэффициентом Пуассона σ и плотностью ρ (Гурвич И.И., 1962):

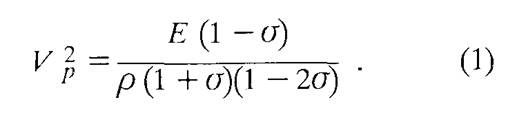
Это уравнение справедливо для большинства горных пород, если деформации и напряжения не слишком велики, поскольку чем меньше величина наблюдаемых деформаций, тем ближе реальная горная порода по своим сейсмическим свойствам к абсолютно упругому телу.

Будем считать, что при проведении сейсморазведочных работ по современным многократным системам наблюдений на некотором реальном расстоянии от источника возбуждения упругих колебаний это условие выполняется.

Нефтегазоперспективные осадочные терригенные и карбонатные отложения отличаются от сплошной абсолютно упругой изотропной среды прежде всего наличием пористости, занимающей часть объема породы.

Зерна породы независимо от их формы, соприкасаясь друг с другом, образуют минеральный скелет, для которого при указанном допущении о существующих реально слабых напряжениях и деформациях справедливо уравнение (1).

По определению модуль Юнга Е = F/S, где F - растягивающая (сжимающая) сила; S - поперечное сечение испытуемого образца. Для пористой породы значение модуля Юнга запишем как Е₀ = F/S₁, где E₀ - некоторое приведенное значение модуля Юнга; F - та же сила; S₁ - площадь сечения того же образца, занятая сплошной средой минерального скелета породы. При этом очевидно, что S₁ = S - S*m, где S - поперечное сечение испытуемого образца; m - пористость.

Тогда

F = E₀S₁ =E₀S(1-m) (2)

Если в выражение Е = F/S подставить значение F из уравнения (2), получим

Е =E₀S (1 -m)/S =Е₀ (1 - m). (3)

Подставляя значение Е из уравнения (3) в уравнение (1), получаем

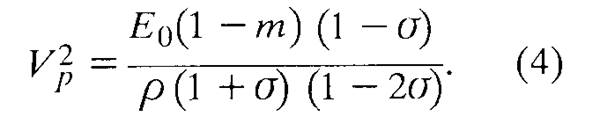
Для простоты дальнейшего изложения обозначим

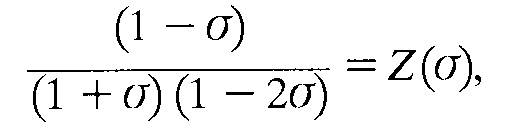
тогда уравнение (4) будет иметь вид

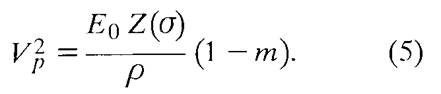
Очевидно, что в сплошной среде m = 0 и, следовательно, Е₀ = Е, тогда уравнение (5) записывается в виде исходного уравнения (1).

Из уравнения (5) следует, что скорость распространения продольной волны определяется не только упругими свойствами пористой горной породы, но и ее общей пористостью. Поскольку исходная геологическая модель продуктивных отложений предполагает постоянство их минерального состава, т.е. неизменность скелета породы, характеризующие его компоненты уравнения (5) E₀, Z(σ) и ρ можно считать постоянными и тогда справедливо записать

E₀Z(σ)/ρ = А = const.

Отсюда

Общая пористость продуктивных отложений m, входящая в уравнение (6), является некоторой усредненной величиной и ее можно представить как

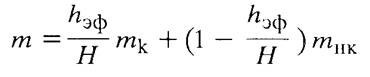
или

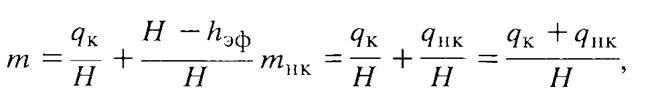
где q_К - эффективная удельная емкость коллектора;

q_нк - удельная емкость неколлектора.

Или то же, но по-другому:

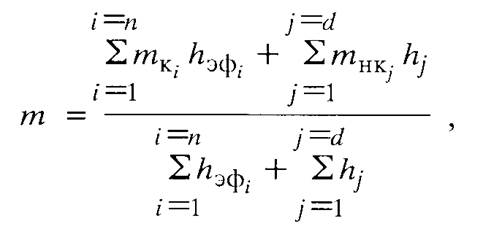
где hj - толщина j-го пласта неколлектора.

Имея в виду тот же смысл величин q и Н, запишем:

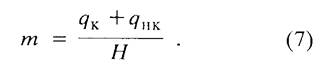
В неколлекторе из-за малого размера пор поровый флюид тесно связан поверхностными силами с поверхностью скелета. Это заставляет его колебаться под воздействием сейсмического возбуждения с частотой, близкой к частоте колебаний твердой фазы. Поэтому флюид, заполняющий поровое пространство неколлектора, ведет себя аналогично твердому телу и не создаст дополнительных препятствий для прохождения сейсмической волны. Напротив, флюид в поровом пространстве коллекторов ведет себя как истинная жидкость или газ, что существенно влияет на волновое сопротивление в насыщенной им пористой среде [1].

Следовательно, величина V_p зависит главным образом от q_к, поэтому, игнорируя q_нк, последнюю можно отнести к разряду констант.

В таком случае уравнение (7) запишем в виде

m = (qk+B)/H  (8)

где В = const = q_нк.

Подставляя уравнение (8) в уравнение (6), получим

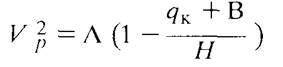
или

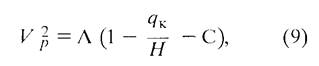
где С = В/H = const.

Отсюда из уравнения (9)

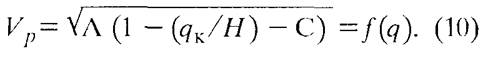
Поскольку при геологической интерпретации сейсморазведочных данных абсолютные значения детальной (псевдоакустической) характеристики разреза особого значения не имеют, а важны ее изменения, т.е. Δv относительно минимальных (Vmin) или максимальных (Vmax) значений скоростей, которым соответствуют повышенные или пониженные емкостные свойства коллекторов, примем, что Vp⁰ соответствует qk⁰, a V_p = qk.

Тогда

Уравнения (10) и (11) хорошо объясняют выявленный в работах [3, 4] факт наилучшего отображения в сейсмических параметрах Δt, ΔV не отдельно пористости или эффективной толщины коллекторов, а их произведения, т.е. параметра эффективной удельной емкости.

При hэф = Н, т.е. сплошном однородном коллекторе, что в геологической практике встречается не так часто,

Таким образом, сплошной однородный коллектор и в геологическом, и в аналитическом плане - частный случай рассматриваемой геологической модели продуктивных отложений, практически решенный ранее (Пузырев Н.Н., 1959). Действительно, в этих условиях скорость распространения продольных волн есть функция пористости коллекторов. Когда коллектор не сплошной, а имеет место продуктивная толща, состоящая из коллекторов и неколлекторов, скорость есть функция произведения пористости на эффективную толщину. При фактическом несоблюдении сделанных допущений в процессе получения уравнений (10) и (11), когда на скорость распространения продольных волн оказывают влияние другие факторы, главным образом изменение минерального состава продуктивных отложений (карбонатизация, глинизация), при установлении зависимости скорости от емкости, в случае низкочастотного характера этих помех относительно более высокочастотного влияния емкости, имеется средство их подавления в виде корреляционного метода (В.С. Славкин, 1994).

Принципиальная важность уравнений (10) и (11) заключается в том, что они достаточно строго с точки зрения теории распространения упругих колебаний и геологических понятий связывают изменения скорости распространения продольных волн не со средней пористостью продуктивных отложений, а с величиной, которая непосредственно используется при установлении объема залежи УВ и подсчете запасов, - эффективной удельной емкостью коллекторов в виде q = m _к *hэф. Это в свою очередь является теоретическим обоснованием методики и технологии определения емкостных свойств коллекторов в межскважинном пространстве по данным сейсморазведки, значительно повышающим достоверность емкостных моделей месторождений нефти и газа.

ЛИТЕРАТУРА

1. Арье А.Г. Физические основы фильтрации подземных под. - М.: Недра, 1984.

2. Крылов Д.Н. К оценке определения литологии и коллекторских свойств по данным сейсморазведки //Геология нефти и газа. - 1992. - № 3. - С. 27-32.

3. Нур А. Использование сейсмических свойств горных пород для изучения и мониторинга пластов-коллекторов. Сейсмическая томография /Пер. с англ. Под ред. Г. Нолета. - М.: Мир, 1990. - С. 213-250.

4. Е.Л. Копилевич, В.С. Славкин, К.С. Шарапова и др. Определение параметра удельной емкости коллектора в межскважинном пространстве // Геология нефти и газа. - 1988. - № 8. - С. 37-40.

5. Neff D.B. Amplitude map analysis using forward modeling in sandstone and carbonate reservoirs //Geophysics. - 1993. - Vol. 58. - № 10. - Р. 1428-1441.

 

ABSTRACT

In the majority of cases, studying of porosity and permeability properties of oil/gas reservoirs is concerned not with continuous uniform reservoir but with productive strata consisting of reservoirs and nonreservoirs. Average porosity value of such productive strata which is estimated by seismic survey data in interwell space, even if provides a characteristic of its properties, cannot be used in determining of pools volume and in reserve calculation. This requires to know about porosity of reservoirs and their effective thicknesses. At the same time, neither porosity nor effective thicknesses are failed to be rather stable estimated by seismic amplitude values, however, the product of porosity by effective thicknesses, that is reservoirs's effective storage capacity, is well correlated with seismic amplitude of all the numerous types of sections studied. Nevertheless, theoretical aspects of validity and necessity to use the product of porosity by effective thicknesses as an universal factor when determining the change in velocity of longitudinal waves propagation in productive carbonate and terrigenous deposits up to now have not been considered. The present article is an attempt to fill the gap and to substantiate the obtained experimental phenomenon from the viewpoint of modern theory of longitudinal seismic waves propagation. The author presents a number of equations supporting the fact that the velocity of longitudinal waves propagation in discontinuous reservoir is a func tion of the product of porosity by effective thickness.