|
УДК 519 553.98 |
© А .В. Долгунин, 1996 |
РОЛЬ ФРАКТАЛЬНЫХ ПОНЯТИЙ В ИССЛЕДОВАНИЯХ ПО ГЕОЛОГИИ НЕФТИ И ГАЗА
А.В.
Долгунин (Институт геологии СО РАН)Одно из понятий о фракталах, которое ввел в современную науку французский математик Бенуа Мандельброт
(Mandelbrot В В The Fractal Geometry of Nature - San Francisco Freeman, 1983), следующее: фракталы характеризуются сосуществованием различимых черт любого допустимого линейного масштаба, от нуля до размера самого объекта или его части, заключенной в рассматриваемом объеме. Это понятие созвучно представлениям о мире, в котором явления различных пространственных и временных масштабов, от самых микроскопических до самых гигантских, отличаясь в частностях, повторяют друг друга в своих главных чертах. Самоподобие, атрибут фрактальной геометрии, встречается в природе повсюду.Фрактальные понятия "наводят мосты" между науками о Земле, математикой и другими отраслями знаний, которые в совокупности изучают с разных сторон одно и то же: природу – единую в многообразии своего проявления.
Ключ к разрешению многочисленных проблем наук и технологий – в применении новых научных подходов, важной частью которых является фрактальная геометрия, тесно переплетающаяся со всем тем, что ныне называется "нелинейная наука" и даже "новая научная парадигма". Американский институт физики в Нью-Йорке
(AIP) издает специальный журнал "Chaos" с подзаголовком "Междисциплинарный журнал нелинейной науки".За рубежом в области наук о Земле вышло несколько сборников статей [4,5], охватывающих широкий круг вопросов, в который, однако, пока не входит геология нефти и газа. В нашей стране можно отметить значительный прорыв в применении фракталов в газонефтяной технологии (Хисамутдинов Н.И. и др., 1994). В докладах Академии наук вышли статьи по нефтегазовой геологии, позволяющие утверждать, что такие исследования начаты [1,3]. Вместе с тем еще в 80-х гг. проведены исследования и построена теория протекания [2], которая может быть использована для фрактального моделирования нефтегазоносных структур.
В местах скоплений углеводородов имеются, как правило, три среды – газ, нефть и вода, заполняющие пустоты пористой среды – породы, обладающей фрактальными свойствами. Границы между средами – ГНК и ВНК – проходят каждая примерно на одной и той же глубине. При более детальном рассмотрении обнаруживается их фрактальная структура со сложными взаимопроникновениями граничащих сред друг в друга. Образующиеся при этом формы можно уподобить изрезанным береговым линиям материков с многочисленными островами и островками разных размеров, мысами и фиордами. Равновесие, в котором находится эта система, локально устойчивое, т.е. нарушается, когда воздействие извне превышает некоторое свое критическое значение. Это может произойти при разработке месторождения, и тогда объект ведет себя малопредсказуемым образом. Но и при разведке месторождений, пока не будет выполнен определенный объем геолого-геофизических исследований, т.е. поставлено большое число очень дорогостоящих экспериментов, трудно составить достоверную модель залежи. При изучении фрактальных свойств объектов обнаруживаются неожиданные
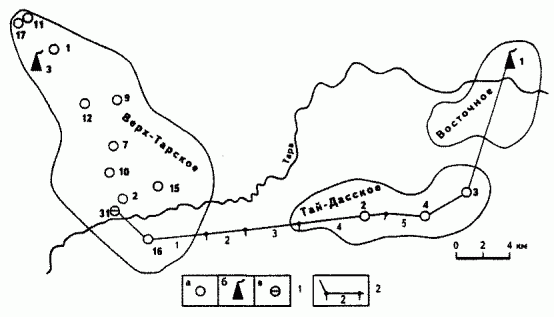
закономерности, объединяющие иногда самые различные процессы и тут же как бы "предлагающие" простые и изящные математические и физические модели для их описания.Примером может служить исследование фрактальной размерности верхней части палеозойских отложений по сейсмическому профилю, проходящему через месторождения Верх-Тарское, Тай-Дасское и Восточное в Новосибирской области (
рис. 1).Фрактальная размерность – величина, имеющая много определений и способов вычисления [2]. В данном случае важным ее свойством является то, что она входит в соотношения вида
f(e) = СeD,
где
f - некоторая величина, зависящая от e, обычно характеризующей линейный размер;С - некоторый постоянный коэффициент пропорциональности;
D - фрактальная размерность.Если прологарифмировать это равенство, то в логарифмическом масштабе по
e и f мы получим линейную зависимость с коэффициентом пропорциональности D:1n f(e) = 1nС + D lne.
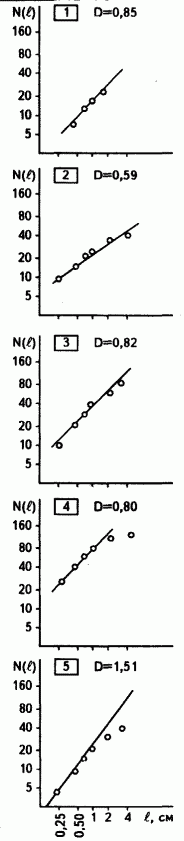
Это свойство и использовалось в расчетах. По сейсмическому профилю (
рис. 2) в пределах выделенных блоков палеозойского фундамента проводился подсчет отражающих площадок разных размеров. Результаты обработки пяти из этих блоков представлены в виде графиков (рис. 3). Четыре и более точек, соответствующих разным размерам площадок, лежат на одной прямой, наклон которой в каждом случае и дает значение D.При анализе полученных значений выяснилось, что
D резко меняется от участка к участку, если имеется предполагаемый разлом или профиль делает достаточно крутой поворот, и остается примерно тем же, если отсутствуют оба эти фактора. Кроме того, если между двумя блоками с близкими значениями D находится третий, имеющий другое значение D, то есть основания предполагать наличие синклинальной складки, объединяющей первые два блока (см. рис. 2, блоки 1 и 3 – эту структуру можно проследить в виде дуги в сейсмической записи).Можно предположить, что значение
D связано с динамикой процессов, происходивших в толще пород, и в связи с этим использовать близость численных оценок D как один из критериев сходства или различия участков.Более того, если рассматривать размер
l отражающей площадки на профиле как характерный линейный размер проходящего в этом месте фрактального кластера размерности v, то масса, или количество субстанции, которая его образует, пропорциональна lv . Тогда количество кластеров этого размера пропорционально Ml/lv, где Мl – суммарная масса субстанции, из которой образовались кластеры размера l. Причем Мl может характеризоваться кубической зависимостью от l, т.е. вещество собрано в кластеры с некоторого кратного l3 объема породы, а v может быть одним и тем же даже для разных веществ, из которых образуются кластеры, в силу единообразия динамики процессов перемешивания. Тогда характеризуемое таким способом значение D равняется 3 - v и все полученные значения хорошо укладываются в диапазон, фигурирующий в теории протекания (v < 1,89 для р < рс = 0,59, где р в нашем случае – характеристика проницаемости пород, а рс – критическое ее значение, когда возникающий кластер начинает заполнять весь отводимый ему объем; интервал 1,89-2,50 указывает на постепенный переход от преобладания плоских кластеров к трехмерным [1]). Необходимо отметить, что теория протекания была разработана как на газожидкостных моделях (вода, заполняющая решетку из ячеек, из которых откачан воздух; воздух, вытесняющий глицерин; вода, вытесняющая несмачиваемую жидкость, например нефть и др.), так и компьютерных, причем все перечисленные процессы обнаружили удивительное сходство своих фрактальных свойств. Вместе с тем эту теорию можно применить и для процессов в твердых телах, поскольку при достаточно больших масштабах времени твердые тела проявляют себя как пластичные и "текут" подобно жидким. Что же касается масштабов пространственных, то здесь для фрактальных исследований доступен и микро- , и макроуровень, что явствует из самой сути фрактальных понятий.ЛИТЕРАТУРА
There are generally exist three media in areas of hydrocarbon accumulations - oil, gas and water filling up the cells of porous medium displaying fractal properties, with two interfaces -gas-oil contact and water-oil contact, each passing roughly at the same depth, however under more detailed examination - having a fractal structure with complicated interpenetrations of bordering media.
Studying of fractal properties allowed to reveal some unexpected regularities which sometimes combine a great variety of processes and simultaneously "offering" a simple and elegant mathematical and physical models to describe them. This may be exemplified by studying of fractal dimensionality of upper Paleozoic deposits by seismic profile running across the Verkh-Tarskoje, Tai-Dasskoye and Vostochnoye fields in Novosibirsk area. One may assume that the blocks divided by faults have different values of fractal dimensionality. These values are expected to be connected with dynamics of processes in rocks formation and may be used as one of criteria of similarity or difference of the sites. An attempt was made for rough description of results in terms of fractal clusters and percolation theory being generalized for large time intervals in case of solids interaction.
Рис.1. СХЕМА РАСПОЛОЖЕНИЯ МЕСТОРОЖДЕНИЙ

1 -
скважина а - глубокая, б - продуктивная палеозойская, в - проектная, 2 - линия сейсмопрофиля с номерами условных блоковРис.2. СЕЙСМИЧЕСКИЙ ПРОФИЛЬ ПО ЛИНИИ СКВАЖИН 16 ВЕРХ-ТАРСКАЯ - 4 ТАЙ-ДАССКАЯ
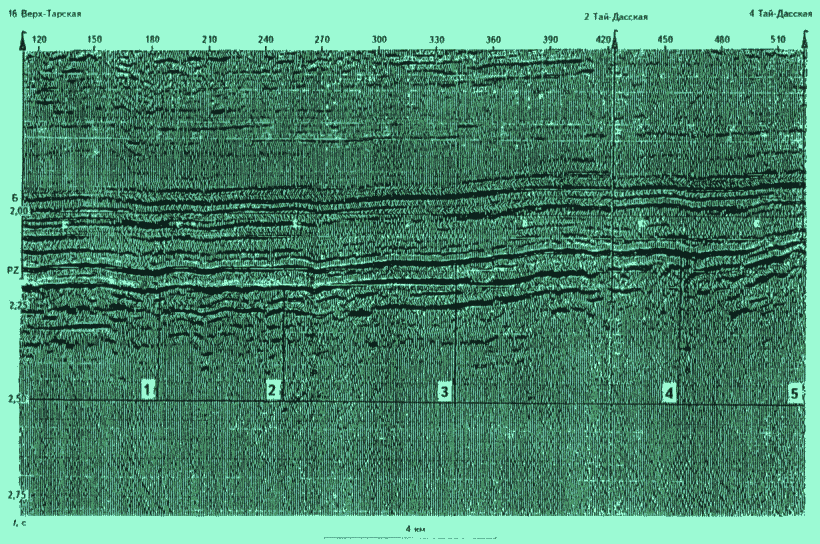
1-5 -
номера условных блоковРис.3. ГРАФИКИ ЗАВИСИМОСТИ ЧИСЛА ПЛОЩАДОК N УСЛОВНОГО БЛОКА ОТ РАЗМЕРА
l