
УДК
550.831.015:553.98.061.4 © П.А.Петренко, С.А.Варягов, А.А.Ярошенко, 1997ПРОГНОЗИРОВАНИЕ НАЧАЛЬНОГО ПЛАСТОВОГО ДАВЛЕНИЯ
П
.А. Петренко (ИГиРГИ), С.А.Варягов, A.A. Ярошенко (Ставропольский ГТУ)Установление роли различных природных факторов в формировании потенциальной энергии геофлюидодинамических систем способствует разработке надежной модели прогнозирования термобарической обстановки недр. Наиболее актуальное значение эти сведения приобретают для регионов, в которых флюидоносные горизонты характеризуются сверхгидростатическими пластовыми давлениями (СГПД), поскольку последние часто приводят к аварийным ситуациям в процессе бурения скважин.
На сегодняшний день разработано значительное число гипотез генезиса начальных пластовых давлений (НПД), в частности сверхгидростатических. Влияние гравитационного фактора обычно рассматривается исследователями как переход (трансформация) геостатической нагрузки (давления) в НПД без учета изменения гравитационного поля во времени и пространстве, т.е. g(x, у, z, t) = const (Александров Б.Л., 1987; Аникиев К.А., 1971; Добрынин В.М., Серебряков В.А., 1989; Магара К., 1982; Фертль У.Х., 1980; Mouchet J.-P, Mithell A., 1989; [5]). Воздействие неоднородного гравитационного поля на НПД впервые проанализировано в работе [1].
Рассмотрим поведение геофлюидо-динамической системы (ГФДС) в гравитационном поле, одним из параметров которого является ускорение свободного падения (У СП).
Под ГФДС авторы данной статьи понимают совокупность взаимосвязанных и взаиморегулирующихся пространственно-временных элементов Земли с заключенными в них динамически активными флюидами, характеризующимися общими условиями создания и раз вития потенциальной энергии, величина которой определяется НПД в единице объема рассматриваемой системы. При выводе зависимости НПД от УСП используется равенство силы потенциальной энергии ГФДС силе тяжести
dFп = dFg,
(1)где
dFп - единичная сила потенциальной энергии флюида.
Тогда, подставляя уравнения
(2) и (3) в выражение (1), получим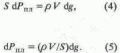
В уравнении
(5) плотность флюида является функцией от Рпл.
Подставляя уравнение
(6) в выражение (5) и обозначая r0Кр V/S через K' , получимdPпл/Pпл = K'dg
. (7)Уравнение
(7) является исходным положением физической генетической модели — метода пропорциональных эффектов, применявшегося ранее весьма успешно для решения физических, биологических, геологических и других задач (Буряковский Л.А., Джафаров И.С., Джеваншир Р.Д., 1982; Миддлтон Г.С., 1968). Полагая в соответствии с методом пропорциональных эффектов, что бесконечно малое изменение НПД (dPпл) при бесконечно малом изменении УСП (dg) пропорционально НПД (Рпл), достигнутой при g, получимdPпл/Pпл(Рм - Рпл) = Кg dg,
(8)где Рм
- максимально возможное НПД ГФДС, принимаемое равным пределу прочности пород, МПа. (Значение этого давления можно установить в соответствии с вещественным составом пород или определить по образцам керна в результате лабораторного эксперимента);Кg,
- коэффициент пропорциональности (МПа*м/с2 )-1 , т.е. имеет размерность, обратную размерности скорости изменения интенсивности энергии (скорости изменения энергии, приходящейся на единицу площади в единицу времени, Дж/м2*c2).Величина (Рм
— Рпл) введена для ограничения возрастания НПД некоторой максимальной величиной, выше которой происходит разрядка потенциальной энергии, т.е. флюидоразрыв. Из уравнения (8) после интегрирования по Рпл в пределах от p0 до Рпл при изменении УСП от g0 до некоторого фиксированного значения g, получим:
Преобразовав уравнение
(9), получим в окончательном виде уравнение взаимосвязи НПД и УСП:
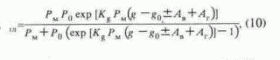
где р
0 - минимально возможное НПД, равное атмосферному (0,1 МПа);g - значение УСП в недрах, м/с ;
g0 - минимальное значение УСП на поверхности Земли в рассматриваемом районе, м/с2;
Ав, Аг - мгновенное ускорение перемещения ГФДС соответственно вертикальное и горизонтальное, м/с
.УСП отражает не только непосредственное влияние неоднородного гравитационного поля на потенциальную энергию ГФДС, но и воздействие других факторов формирования НПД, таких как напряженно-деформированное состояние коллектора, фильтрационно-емкостные свойства пород и др.
[2, 4 ].В уравнение
(10) Aв входит со знаком плюс, если его вектор сонаправлен с вектором УСП, при противоположном направлении — со знаком минус. (±Ав + Аг) представляет собой поправку, вносимую в УСП за счет ускоренного движения ГФДС, на необходимость которой указывают исследования И.М.Михайлова. "На Северосохском месторождении (опускающаяся часть впадины) давления вод в пластах палеозойского, юрского и нижнемелового возраста примерно на 2,5 МПа выше расчетных гидростатических. В тех же самых отложениях на месторождении Андижан-Ходжиобад (воздымающаяся адырная зона) они на 0,8-1,0 МПа ниже расчетных гидростатических.., на других месторождениях Ферганы зависимость изменения пластовых давлений от направленности новейших движений земной коры аналогичная" [5, с. 22 ]. Коэффициент пропорциональности (Kg) между ускорением и НПД, выполняющий роль "подгонки" абстрактной физико-математической модели к природной, содержит информацию о латерально-вертикальной раскрытости ГФДС, тектонической и сейсмологической обстановках, структурных особенностях пустотного пространства породы-коллектора, морфологии формационных комплексов и др.Внешнее гравитационное поле, интерферируясь с внутренним, трансформирует структуру флюида, что отражается в незначительной вариации радиальной функции распределения молекул воды
G(r), изменение которой от температуры приведено на рис. 1. В свою очередь это оказывает влияние на давление в системе, которое чрезвычайно чувствительно к колебанию G(r) (Темперли Г., Роулинсон Дж., Раушбрук Дж., 1971). Жидкости, находящиеся в естественных условиях земных недр, можно рассматривать как квазиполимерные вещества, молекулярные цепи которых создают дальнодействующие корреляции. В связи с этим для таких систем характерны сильные флуктуационные эффекты, аномально малая энтропия и соответственно аномальная восприимчивость к внешним воздействиям. Кроме того, необходимо учитывать, что присутствие в воде различных веществ (ионы, газы, органические и коллоидные вещества) вносит существенные изменения в физико-химические свойства подземных вод в природных условиях, перестраивая их структуру и поле потенциальной энергии взаимодействия молекул (рис. 2).Компоненты Ав и Аг можно разложить на четыре составляющие: тектоническую, техногенную, приливную, сейсмическую. В этом ряду продолжительность их воздействия убывает в порядке перечисления. Надежные сведения о них в настоящее время не получены. Оценочные данные об ускорениях при землетрясениях (
рис. 3, таблица) свидетельствуют о том, что сейсмическая компонента вносит значительный, правда, кратковременный вклад в изменение НПД, носящего черты гидроудара и могущего приводить к флюидоразрыву. Характер затухания ускорения в пространстве показывает, что на расстоянии 100 км от эпицентра землетрясения ускорение перемещения грунта составит около 100 мкм/с2 (рис. 4). Остается без ответа вопрос о реакции подземных вод на кратковременные воздействия ускорений перемещения ГФДС, так как жидкости в подобной обстановке могут проявлять черты квазитвердого тела.На
рис. 5 показаны зависимости НПД от УСП без учета ускорений перемещения ГФДС на примере Лесной, Махач-Аульской, Южно-Ачикулакской, Ямангойской, Кунайской площадей, расположенных на южном склоне Прикумской системы поднятий Восточного Предкавказья. Значения НПД замерялись глубинными манометрами в водоносной части какого-либо горизонта, а значение УСП определялись из уравнения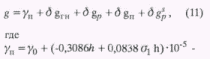
где
h - превышение поверхности Земли над поверхностью геоида, м;s1
- средневзвешенная плотностьпород в интервале 0-h, кг/м3 ;g
о - нормальное значение УСПна поверхности геоида [3].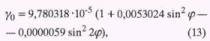
где
j - географическая широта, град;d
gгн - наблюденная аномалия УСП на поверхности Земли, м/с2 ;

Формулы
(13), (15) основаны на замене верхней части разреза плоскопараллельным слоем. В них не учтено изменение нормального вертикального градиента в зависимости от широты. Для учета этого изменения используется следующее выражение [3 ]: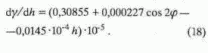
Для повышения точности редуцирования гравитационного поля необходимо принимать во внимание также аномальный вертикальный градиент (Hammer
S., 1970). В районах со сложным геологическим строением (при наличии в разрезе контрастных плотностных границ со сложной геометрией поверхности) редуцирование производится дискретно на каждую структурную поверхность с последующим введением поправки за глубинный рельеф этой поверхности. Введение этой поправки преобразует модель со сложным геологическим строением в модель плоскопараллельных слоев. Сложные по форме и распределению масс тела в случае непостоянства плотности по площади одного горизонта разбиваются на части таким образом, чтобы их влияние можно было определить аналитически, затем суммируют влияния частей тела и находят поле, создаваемое всем телом.Значения
Kg получали из заданных Pм, p0, замеренных g0, Рпл* и расчетных g*, полученных на площадях, изученных бурением и характеризующихся сходным геологическим строением: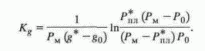
По характеру зависимости потенциальной энергии от УСП выделяются два типа ГФДС:
ГФДС-1
— НПД с возрастанием УСП увеличиваются (см. кривую 5 на рис. 5);ГФДС-2
— НПД по кровле горизонта с увеличением УСП уменьшаются (см. кривую 1 на рис. 5), но в каждой конкретной точке площади НПД по разрезу с увеличением УСП возрастают (см. кривые 2-4 на рис. 5). Кривые 2-4 иллюстрируют зависимость НПД от УСП по разрезу в точках площади, для которых характерно равенство g на глубине залегания кровли горизонта. Потенциальная энергия ГФДС двух типов описывается одним и тем же уравнением (10), но коэффициент пропорциональности Kg входит в уравнение со знаком плюс для ГФДС-1, ГФДС-2 (по разрезу) и со знаком минус для ГФДС-2 (по кровле горизонта). ГФДС-1 отличается от ГФДС-2 большей способностью релаксировать по площади НПД в случае их изменения и, следовательно, большей латеральной раскрытостью. ГФДС-2 — это инжекционные системы с резко неоднородной по площади проницаемостью.УСП можно представить функцией времени
g(t), отвечающей полигармоническому процессу и определяемой суперпозицией синусоидальных колебаний: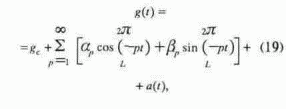
|
|
постоянное значение УСП, при котором происходит неприливная вариация исходной зависимости g(t) |
|
амплитуды гармоник (коэффициенты Фурье); |
|
|
номер гармоники |
|
|
текущее значение времени |
|
|
максимальное время наблюдения |
|
|
случайная функция, отражающая негармоническое кратковременное влияние различных факторов (например, сейсмичности) |
Анализируя формулы
(10), (19), можно сделать вывод, что НПД должны испытывать гармонические вариации с сопоставимыми частотами или периодами. Это подтверждается режимными наблюдениями за изменениями уровня подземных вод и УСП на поверхности Земли (рис. 6). Временные вариации НПД ГФДС-1 синфазны вариациям УСП. Для гармонических колебаний НПД (по кровле горизонта) ГФДС-2 характерна антифазность (скв. 324). Локальные несоответствия объясняются постановками различных задач при вариационных наблюдениях за НПД и УСП, различиями в методологии проведения работ.Рассмотренная физико-математическая модель позволяет объяснить следующие факты, для описания которых ранее создавались отдельные модели:
2) НПД на одной и той же глубине выше на тех площадях, разрез которых сложен менее плотными породами, например передовой прогиб и платформа, что хорошо видно из уравнения (14);
3) зависимость НПД от структуры перового пространства породы-коллектора учитывается (V/S);
4) временные полигармонические колебания уровня подземных вод (уравнения (10) и (19).
Необходимо отметить, что изучение влияния неоднородного гравитационного поля на потенциальную энергию ГФДС требует постановки исследований НПД и УСП на единой целевой и методологической базе с привлечением данных гравиметрического каротажа.
Методика прогнозирования НПД в водоносных горизонтах, построенная на основе вышеописанной модели, заключается в следующем.
На площади, не изученной бурением, проводят гравиметрическую съемку и сейсморазведку, что позволяет получить морфологические параметры и глубину залегания различных горизонтов. Плотность пород определяется по сейсморазведочным данным из корреляционного уравнения:

Средневзвешенная по разрезу плотность находится как
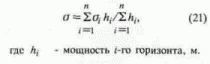
Например, для территории Татарстана средние значения коэффициентов регрессии следующие: а
= 1,750; b = 0,266; с = -0,015. Ошибка определения плотности для трех слоев (промежуточного между дневной поверхностью и уровнем моря, между уровнем моря и жесткой сейсмической границей — кровля сакмарского яруса нижней перми, между последней границей и кровлей ассельского яруса нижней перми) соответственно составила ±0,04, ±0,03, ±0,02 г/см3. В дальнейшем, используя эти данные и уравнения (11)-(18), рассчитывают УСП по разрезу и площади, а НПД находят из выражения (10), в котором Kg определен для площадей, изученных бурением и характеризующихся сходным геологическим строением с прогнозируемой площадью. Для ГФДС нижнемеловых — палеозойских отложений Лесной, Махач-Аульской, Южно-Ачикулакской, Ямангойской, Кунайской площадей зависимость Kg от УСП имеет следующий вид:

ЛИТЕРАТУРА
1.
Влияние гравитационного поля на потенциальную энергию флюидодинамических систем / Ш.Ф.Мехтиев, З.А.Буниат-Заде, Ю.А.Стерленко и др. // Азербайджанское нефт. хоз-во. - 1990. - № 6. - С. 24-28.2.
Гидродинамическая реакция водоносного горизонта на изменение его напряженного состояния / Г.С.Вартанян, В.И.Башмаков, В.О.Волейшо и др. // Сов. геология. - 1987. -№ 7. - С. 110-115.3.
Гравиразведка: Справочник геофизика / Под ред. Е.А.Мудрецовой, К.Е.Веселова. -М.: Недра, 1990.4.
Локальные вариации силы тяжести в результате вибровоздействия / Ю.Д.Буланже, Т.В.Гусева, Т.Е.Демьянова и др. // Докл. АН СССР. - 1990. - Т. 311, № 4. - С. 835-838.5.
Михайлов И.М. Потенциальная энергия пластовых флюидов. - М.: Наука, 1987.
I -
Н2О; II - Cl; 111 - Li; расстояния между ядрами: 1 - О-Н2; 2 - O-O; 3 - O-Cl; 4 - O-Li (возле кривых показаны соответствующие им ориентации молекул Н2О)Количественные параметры интенсивности колебаний (по Джибладзе Э.А.,
1980)|
Интенсивность, балл |
Интервал максимальных ускорений грунта, см/с 2, при периоде 0,1 с и более |
Интервал максимальных скоростей колебаний грунта, см/с |
Интервал максимальных смещений центра тяжести маятника сейсмометра СБМ, мм |
|
6 |
30-60 |
3,0-6,0 |
1,5-3,0 |
|
7 |
61-120 |
6,1-12,1 |
3,1-6,0 |
|
8 |
121-240 |
12,1-24,0 |
6,1-12,0 |
|
9 |
241-480 |
24,1-48,0 |
12,1-24,0 |
Изменение ускорения свободного падения:
I - в Севре ( по данным А.Сакумы), II - на пунктах Ледово -Потсдам - Новосибирск по измерениям гравиметром ГАБЛ (Буланже Н.Д., 1983); 1-3 - осредненные кривые изменения среднегодового уровня вод по скв. 324, 2/51, б соответственно (Гавич И.К., Ковалевский B.C., Язвин Л.С., 1983)
On the basis of consideration of a geofluiddynamic system behavior in non-uniform non-stationary gravity field a relationship of potential energy of geo-fluiddynamic system versus gravity acceleration including gravity field distribution in the subsurface, instant vertical and horizontal accelerations of geofluiddynamic system movement was obtained.
A value of gravity acceleration reflects not only a direct influence of non-uniform gravity field on potential energy of geofluiddynamic system but the effect of other factors in forming initial formation pressures such as stressed-defonned state of reservoirs, porosities and permeabilities properties of rocks.
Two types of geofluiddynamic systems by a character of relationship of potential energy versus gravity acceleration are distinguished. Shown is a comparability of temporary variations of ground water levels and gravity acceleration on the Earth's surface.
A procedure to forecast initial formation pressures in aquiferous horizons based on geological, petrophysical data and on the results of gravity and seismic survey was proposed.