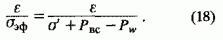
|
УДК 551.2.02 |
© И.Ф. Радковец, 1997 |
ОБ ЭФФЕКТИВНОМ НАПРЯЖЕНИИ И ОПЫТАХ ТЕРЦАГИ
И.Ф.
Радковец (ЗапСибНИИгеофизика)Связь между горным давлением Ргор, напряжением в скелете породы Рск (иначе его называют эффективным) и давлением в насыщающей жидкости Рпл описывается широко известной формулой [1,2,4]
Ргор
= Рск + Рпл (1)(здесь и далее Ргор и Рск означают вертикальные составляющие указанных параметров) .
При записи уравнения (1) обычно рассуждают следующим образом. Пластовое давление жидкости способствует уменьшению нагрузки, передающейся на скелет породы от массы вышележащих отложений (если кровля пласта непроницаема) [1, с.67]. Тогда давление на скелет породы будет равно:
Рск
= Ргор – Ррпл (2)Параметры Ргор и Рпл определяются выражениями
Pгор=dГПgH, (3)
Рпл
=dвgН, (4)где
dГП и dВ - плотность насыщенных горных пород и воды соответственно;g - ускорение свободного падения; Н - глубина до точки определения параметров.Отсюда легко находят Рск
:Рск
=gH(dгп-dВ). (5)Однако значение параметра Рск, вычисленное по формуле (5), значительно меньше фактически существующих напряжений в природе. Видимо, поэтому было решено, что не вся величина пластового давления направлена на разгрузку горного, и поэтому при параметре Рпл в уравнении (1) справедливо появляется коэффициент
n, а формула (2) принимает видРск = Ргор
- n Рпл (6)Однако подлинной причиной нарушения равенств (1) и (2) явилось то, что они записаны вопреки законам физики. Дело в том, что пластовое давление противодействует горному не по всей площади сечения горной породы, а лишь на участках, занятых жидкостью. Поэтому в уравнении (2) давления необходимо выразить через силы и потом уже производить операцию сложения (или вычитания).
Пусть на некотором участке отложений вся площадь горизонтального поперечного сечения пород равна
S, а часть сечения, приходящаяся на пористую среду, равна Sп. Тогда вместо уравнения (2) следует записать:Рск
(S – Sп)= Ргор S - Рпл Sп (7)откуда после ввода нового параметра
– коэффициента просветности, равногоKS=Sп/S, (8)
и после преобразований получим:
Pгор=Рск(1-Ks)+PплKs. (9)
Если произвести вычисление напряжения Рск исходя из формулы (9), то окажется, что оно не только не меньше горного давления, но даже больше него, поскольку противодействующая массе вышележащей толщи сила
FПЛ=РплSп (10)
меньше силы, создаваемой на этих же площадках массой пород
Fгор =Pгор Sп (11)
Fпл не компенсирует Fгор полностью, и эта нескомпенсированная часть в результате будет приходиться на твердую фазу пород, увеличивая в ней напряжение.
Для того чтобы объяснить причину возникновения формул (1) и (2), необходимо рассмотреть их происхождение.
Немецкий исследователь Терцаги на основании лабораторных опытов Рендулика и своих собственных [3] пришел к выводу, что если на пористый образец, помещенный в непроницаемую оболочку, окаймляющую его боковую поверхность, сверху давит столб воды, то при отсутствии разделяющей пластины это давление не вызывает деформации грунта (рисунок). При действии каких-нибудь иных механических сил (например, эквивалентных действию массы свинцовой дроби) слой грунта окажется заметно сжатым. На основании этого Терцаги предположил, что сжимающее напряжение в водонасыщенном грунте включает в себя две составляющие – нейтральное гидростатическое давление Pw и эффективное sэф. Сумму этих давлений он назвал полным
s
= sэф+Pw. (12)Для того чтобы можно было подтвердить это замерами, были произведены испытания образцов по следующей схеме: в дополнение к осевому давлению
s', действующему посредством пластины, было добавлено всестороннее Рвс с помощью сжатого воздуха или глицерина (см. рисунок). К жидкости, насыщающей поры, через фильтрующий камень подсоединены манометр и кран. Так как обе составляющие создают напряженное состояние образца, то было решено, что каждое его горизонтальное сечение испытывает вертикальное напряжение, равное сумме осевого давления и всестороннегоs
г=s'+Рвс, (13)а каждое вертикальное сечение
– только всестороннее давлениеs
II= sIII = рвс (14)На основании таких лабораторных опытов Терцаги и Рендулик сделали вывод, что деформация образца
e и сопротивление сдвигу с зависят от разницы между полным напряжением и давлением в порах Pw, т.е. от эффективного давления:e
=f(sэф) (15)c =f (sэф) , (16)
где
sэф = s'+Pвс-Pw. (17)Получение такого результата лабораторными опытами можно подтвердить и теоретически.
С учетом уравнения (17) найдем частное от деления деформации на эффективное напряжение:
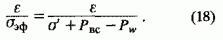
Из определения коэффициента упругости относительная объемная деформация образца
e может быть найдена по формулеe
= s0b0. (19)Назовем породы пропорционально сжимающимися, для которых
e
= eск , (20)В этом случае давление в насыщающей жидкости (Радковец И.Ф., Радковец Н.Л., 1990) определяется уравнением
Pw=s0=b0/bж, (21)
где
b0, bж - коэффициенты упругости горной породы и жидкости соответственно; s0 - среднее напряжение в образце (находится согласно теории упругости), равное: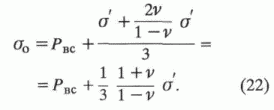
Подставляя выражения (19), (21) и (22) в правую часть уравнения (18), получим:
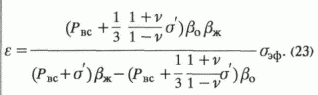
Для прямой пропорциональности между
e и sэф необходимо и достаточно, чтобы соблюдалось условие: e/sэф = const. (24)Найдем предел отношения (24) при V-> 0,5:
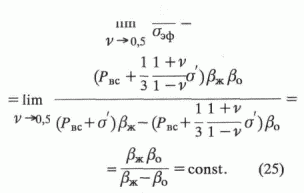
Из уравнения (25) видно, что при коэффициентах Пуассона, равных 0,5, существует прямая пропорциональная зависимость между
e и sэф. С уменьшением значения v зависимость (15) отклоняется от прямой линии.Если относительные деформации
eск и e не равны между собой, то давление в порах может быть представлено общим уравнением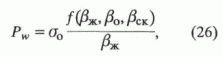
где
bск - коэффициент упругости скелета.Решая аналогичным образом при
V = 0,5, получим также: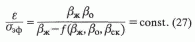
Терцаги и Рендулик работали с грунтами
– песком и глиной. Коэффициенты Пуассона для таких пород довольно велики, поэтому они могли с достаточной степенью точности получить прямую пропорциональную зависимость между eи sэф в некотором небольшом диапазоне изменения внешних сжимающих сил, пока упругие свойства образцов сохранялись постоянными. В других случаях (небольшие значения v, изменяющиеся коэффициенты упругости) зависимость e =f(sэф) должна отклоняться от прямолинейной, но эти случаи не характерны для грунтов, поэтому Терцаги обнаружил только прямую пропорциональность. И поскольку при этом значение e не зависит от Pw, то он и предложил уравнение (12), которое впоследствии было использовано в геологии.Насколько правомерно переносить результаты лабораторных исследований в условия естественного залегания горных пород, в настоящей статье не рассматривается. Но поскольку этот перенос уже осуществлен, уточним, что определяет
sэф для отложений в земной коре. Обратимся к первому опыту Терцаги, когда при отсутствии металлической пластины сверху непосредственно на образец давит столб жидкости (см. рисунок). Отсутствие деформации грунта в этом случае можно объяснить тем, что вода заполняет все поры образца и ее давление, распределяясь по всем направлениям, действует на каждую частицу в отдельности. Последние, деформируясь, уменьшаются в размерах. Следует полагать, что настолько же увеличивается и пористое пространство, поэтому общие размеры образца остаются без изменений. На этом основании Терцаги назвал давление воды нейтральным. Такое же действие оказывает на горные породы в земной коре насыщающая их жидкость. Поэтому пластовое давление также можно назвать нейтральным. Давление же твердой ненасыщенной вышележащей толщи отложений, аналогичное действию свинцовой дроби на образец, деформирует залегающие породы и поэтому его следует называть эффективным. Полное напряжение в этом случае в соответствии с формулой (12) будетs
= sэф+Рпл. (28)Параметр
sэф можно выразить уравнениемs
эф=dскgН, (29)где
dck - средняя плотность скелета вышележащих отложений.Уравнение (28) выражает не суть формулы (1), записанной вначале: параметр
s вовсе не равен Ргор. Это видно из следующего.Для определения
sэф плотность скелета породы можно найти из системы уравнений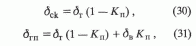
где
dТ - плотность твердой фазы породы Kп - коэффициент пористости,решая которую, получим:
d
ск = гп -ВКП. (32)По известной плотности
ck определяются эффективное и полное напряжения: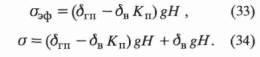
Сравнивая уравнения (5) и (33), (3) и (34), приходим к выводу, что
s
эф>Pск, (35)s
>Ргор. (36)Эти различия, казалось бы, в одинаковых параметрах произошли вследствие того, что общее напряжение, создаваемое массой насыщенной горной породы, не равно полному напряжению, т.е. сумме обеих составляющих, существующих в каждой фазе отдельно. Терцаги лишь ввел понятия полного и эффективного напряжения. Рассмотрим теперь физический смысл каждого из них.
Если толща отложений до некоторой глубины состоит из одних коллекторов, то эффективное напряжение создается только твердой фазой вышележащих пород и действует как вне каждой частицы, сдавливая их между собой, так и внутри частиц. Образуется некоторое среднее напряжение на контакте и внутри всех частиц, вместе взятых. Поэтому оно и оказывает влияние на деформацию и сопротивление сдвигу.
Гидростатическое давление образуется насыщающей жидкостью и действует на каждую частицу в отдельности, не прижимая их друг к другу. Поэтому внутри частиц создается напряжение, равное сумме обеих составляющих, т.е. полное напряжение, а на контакте между ними
– только одно, эффективное.Горное же давление Ргор создается смесью породы с водой и определяется плотностью этой смеси, которая равна не сумме составляющих плотностей, как это следует из уравнений (1)-(5), а сумме их долей. Для определения Ргор необходимо прежде найти суммарную плотность по формуле (31). Тогда
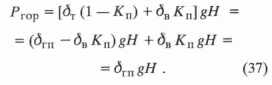
Горное давление (вернее, его вертикальная составляющая) создается под плотным слоем. В этом случае эффективное давление в скелете залегающего ниже пласта-коллектора будет определяться исходя из формулы (9):
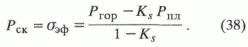
Таким образом, на основании опытов Терцаги можно сделать следующие выводы.
Эффективное напряжение формируется в твердой фазе пористого пласта и определяется двумя факторами:
1. Массой скелета вышележащей толщи, если последняя также пористая; в этом случае
эф находится по формуле (33).2. Массой всей вышележащей толщи, если в кровле коллектора залегает плотный пласт; тогда эф вычисляется по формуле (38).
Сумма эффективного напряжения с пластовым давлением составляет полное напряжение (не равное горному) и соответствует выражениям (28) и (34).
Горное давление Ргор определяется формулой (3) и меньше полного, в результате чего выражение (1) является неравенством
Ргор < Рск + Рпл и должно быть исключено из учебной литературы по физике пласта. Вместо него следует пользоваться уравнением (28).ЛИТЕРАТУРА
The present article deals with the known formula in petrophysics describing a relationship between rock pressure, rock skeleton stress and saturated liquid pressure. Author proves that this formula is against the physics laws and therefore a rated rock skeleton stress appears to be too low, and suggests to exclude it from petrophysics text-books. Considering that formation pressure counteracts rock pressure not over the whole area of rock section but only at localities occupied by a liquid, the author suggests his own solution of the problem and derives a formula complying with physical reality.
СХЕМА ТЕРЦАГИ ДЛЯ ИСПЫТАНИЯ ГРУНТОВ
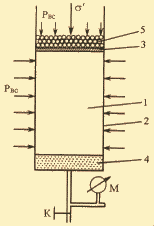
1
- образец; 2 - резиновая оболочка; 3 - металлическая пластина; 4 - фильтрующий камень; 5 - свинцовая дробь; К - кран; М - манометр