УДК 550.344.094.5:553.98.061.4
ОБОСНОВАНИЕ ВОЗМОЖНОСТИ ОПРЕДЕЛЕНИЯ ПРОНИЦАЕМОСТИ ПОРОД ПО СКОРОСТИ ПРОХОЖДЕНИЯ СЕЙСМИЧЕСКИХ ВОЛН
А.Г.
Арье (ВНИГНИ)Проблема определения фильтрационно-емкостных свойств в межскважинном пространстве подземной гидросферы методами сейсморазведки является кардинальной для поисков и разведки нефтяных и газовых залежей. Ей посвящено большое число публикаций как в отечественной,
так и в мировой специальной литературе. К их числу можно отнести работы Н.Н. Пузырева (1959),Е.А. Копилевича, В.С. Славкина, Е.С. Шараповой (1988), Д.Н. Крылова (1992), А. Нура (1990), Д.В. Неффа (1993), Е.А. Копилевича (1995) и многие другие.В этих работах, как правило, затрагивается только одна сторона проблемы, а именно: определение емкостных свойств пород — показателя необходимого, но не исчерпывающего до конца ее содержания. Несмотря на то,
что задача определения емкостных свойств отложений решалась на базе анализа прохождения псевдоакустического возбуждения в водонасыщенной пористой среде, само это обстоятельство — водонасыщенность среды — как правило, оставалось за рамками рассмотрения.Впервые в своих построениях это обстоятельство попытался учесть Е.А.Копилевич [2]. Так, он считает, что в слабопроницаемых отложениях сейсмическая волна
ведет себя как в непористом твердом теле, и на этом основании выделяет емкостную составляющую, относящуюся исключительно к пластам-коллекторам. Тем самым он косвенно показывает, что скорость прохождения сейсмической волны в принципе зависит от проницаемости пористой среды. В качестве основания для такого утверждения использован широко известный факт удержания слабопроницаемыми породами поровых жидкостей в связанном состоянии, по консистенции близком к твердому. Понятно, что предшественники, не учитывавшие этого обстоятельства, имели все основания считать, что скорость прохождения сейсмического возбуждения в геологической пористой среде определяется исключительно пористостью среды и не зависит от ее проницаемости [3].Тем не менее задача оценки проницаемости в межскважинном геологическом пространстве не теряла своей актуальности и вследствие этого работа над ее решением продолжалась. Как правило, главным направлением исследований служила попытка прямого коррелирования параметров пористости и проницаемости. При этом исследователи почему-то упускали из виду, что рассматриваемая корреляция должна учитывать и величину
удельной поверхности, как это следует из известного соотношения Козени — Кармана. Иногда такая корреляция реализуется, но вследствие приведенных соображений это, скорее, частный случай, особенно в тех ситуациях, когда коррелятивная связь оказывается прямолинейной. На основании изложенного это направление исследований нельзя признать теоретически обоснованным и, следовательно, перспективным для достижения поставленной цели.Ближе к решению задачи подошли авторы публикации [4]. В ней на базе измерения эффективной удельной емкости отложений с помощью полевой сейсморазведки в межскважинном пространстве, оценки коэффициентов продуктивности скважин и лабораторного определения усредненных радиусов поровых каналов по керну разведочных скважин показана возможность оценки гидропроводности продуктивного пласта и ее вариаций в соответствии с изменениями эффективной удельной емкости в латеральном направлении. Предложенный подход оказался достаточно результативным. Тем не менее он не лишен некоторых недостатков, подвергающихся, в общем, справедливой критике. Эта критика касается главным образом следующих двух позиций: 1) всегда ли реализуется прямолинейная корреляция между приведенным удельным дебитом скважин и квадратом усредненного радиуса поровых каналов вскрытой ими породы; 2) какова погрешность от экстраполяции значений радиуса поровых каналов, полученных в отдельных точках бурения, в межскважинное пространство. Если по первой позиции можно всегда ответить утвердительно (при корректных измерениях расхода и давления и не слишком больших дебитах скважин), то по второй подобной ясности нет. Действительно, при разнесении значений радиуса поровых каналов по площади распространения коллектора присутствует известная доля субъективизма. Поэтому такой метод решения задачи, несмотря на его достаточную теоретическую мотивированность и безусловную практическую полезность, следует отнести к разряду паллиативных.
Отмеченный недостаток можно исключить, если иметь надежный ориентир, выраженный в измеряемых характеристиках пласта, чтобы с его помощью получить количественное обоснование принципа размещения дискретной информации (например, сведений о величине усредненного радиуса поровых каналов, привязанных к точкам бурения) по всем точкам геологического пространства, в которых выбранный ориентир может быть отслежен.
Таким ориентиром мог бы служить параметр изменения скорости распространения сейсмической волны, выраженный через вариации интервального времени — величины, обратной значению скорости. Преимущество выбора именно этого параметра состоит в том, что интервальное время является единственным непосредственно измеряемым параметром при проведении сейсмического возбуждения пласта, характеризующим процесс прохождения сейсморазведочных волн в геологической среде. Этот показатель фиксируется достаточно густой сетью пунктов наблюдения в межскважинном пространстве и, следовательно, дает возможность оценить "привязанную" к нему характеристику пласта, известную в точке бурения, на всей площади проведения сейсморазведочных работ.
Как упоминалось, скорость сейсмической волны в заполненной жидкостью пористой среде в традиционной постановке задачи, т.е. в неявном предположении о том, что движение поровой жидкости подчиняется закону Дарси, определяется пористостью среды и не зависит от ее проницаемости. Такое утверждение справедливо только для сред, характеризующихся относительно высокими значениями проницаемости
[1]. В общем же случае такая постановка задачи оказывается недостаточно корректной, так как в ней не в полной мере учитывается влияние взаимодействия жидкой фазы с поверхностью скелета минеральной составляющей среды. Если же такое взаимодействие принять в расчет, то вывод о независимости скорости распространения упругой волны в водонасыщенной пористой среде от ее проницаемости оказывается недостаточно убедительным. Рассмотрим этот процесс, используя традиционный алгоритм анализа, применяемый обычно для решения такого рода задач.В рамках выбранного подхода для удобства построений рассматривают время прохождения волны механического возбуждения
t0 через образец длиной l флюидонасыщенной пористой среды, которое определяется выражением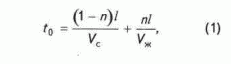
где
n — пористость образца; Vc, Vж — скорость прохождения волны через материал скелета и жидкости соответственно.Если обе части формулы
(1) поделить на l, то в соответствии с определением понятия "интервальное время" получим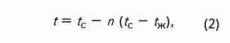
где
t — интервальное время, характерное для всей системы в целом; tc, tж - то же для материала скелета и жидкости соответственно.Из теоретической физики (Китайгородский А.И., 1959) известно, что
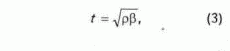
где р — плотность среды, в которой распространяется волна; β - коэффициент ее объемной сжижаемости.
На этом основании формула (2) может быть записана в виде
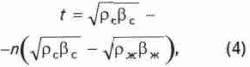
где индексами с и ж отмечены показатели, характеризующие скелет и поровую жидкость соответственно.
Если решать задачу в традиционной постановке, т.е. без учета межфазового взаимодействия, то формула (4) показывает, что, действительно, значение интервального времени,или скорости прохождения сейсмической волны, определяется только свойствами материала скелета и жидкости и пористостью породы.
Рассмотрим эту задачу с учетом сил межфазового взаимодействия поровой жидкости со стенками поровых каналов. С этой целью запишем (4) в виде
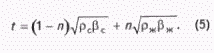
Относительно первого слагаемого формулы можно утверждать, что его значение при прочих равных определяется пористостью горной породы.
Второе слагаемое целесообразно рассмотреть более детально. По определению пористость среды — константа, а вот величина
βζ, по существу, являющаяся коэффициентом упругоемкости пласта (Щелкачев В.Н., 1959), может быть выражена через фильтрационные характеристики пласта, такие как коэффициент проницаемости, коэффициент пьезопроводности среды и вязкость фильтрующейся жидкости:
Такой вид выражение (6) имеет, если считать.что процесс фильтрации подчиняется закону Дарси. Если иметь в виду, что этот закон является частным случаем обобщенного закона фильтрации (Арье А.Г.,
1981)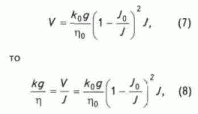
где
V— скорость фильтрации; k0 — коэффициент проницаемости по Дарси, т.е. при J>>J0; J- градиент давлений, развиваемый источником колебаний; J0 - начальный градиент фильтрации пористой среды.Из формулы (8) следует, что величину вязкости можно представить в виде
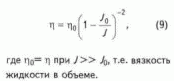
Очевидно
, что при J = J0 вязкость жидкости возрастает и приближается по значению к вязкости твердого тела, так как закон справедлив только в интервале J0<J<=JкрПодстановка (9) в (6) дает:

Этот, казалось бы, физически парадоксальный вывод означает, ЧТО при УСЛОВИИ
J = j0 поровая жидкость целиком переходит в связанное состояние и сжимаемость ее становится "неотличимой" от сжимаемости твердого тела *.Подставляя выражение
(10) в формулу (5), будем иметь: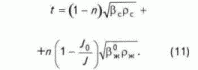
Все компоненты полученной формулы за исключением параметров начального градиента фильтрации и пористости являются константами. Сомнение вызывает лишь градиент давления (напора)
J, физически представляющий собой потенциал, вызывающий движение сейсмической волны в водной составляющей водозаполненной пористой среды. Но, как следует из формулы (3), скорость распространения волн в гомогенной среде определяется двумя постоянными, характеризующими физическое состояние этой среды — в данном случае поровой воды — ее плотностью и сжимаемостью. Следовательно, и скорость прохождения волны через жидкую составляющую системы является константой. В то же время в соответствии с уравнением состояния конденсированных сред Ван-дер-Ваальса процесс передачи давления из точки в точку таких сред, являющийся физической сущностью распространения сейсмической волны, обусловлен перемещением объемов этой среды по тем же ее точкам, по которым проходит волна. Скорость распространения волны тождественна скорости таких перемещений. Поэтому, если она является константой, это значит, что процесс передачи давления реализуется с постоянной скоростью. В пористой среде такое перемещение поровой жидкости подчиняется законам нетурбулентной фильтрации, согласно которым его скорость пропорциональна градиенту давления (напора). Из сказанного ясно, что если указанная скорость постоянна, то это является следствием постоянства градиента давления.С учетом изложенного представляется реальным, каков характер колебания интервального времени в зависимости от изменения пористости отложений. Для этого необходимо продифференцировать формулу
(11) по параметру пористости. Результат дифференцирования имеет вид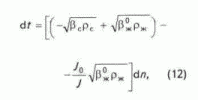
что после перехода к конечным разностям дает
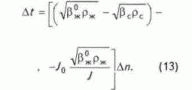

где Сз — некоторая постоянная;
R — усредненный радиус поровых каналов, определяющий значение проницаемости. Следовательно, окончательно можно записать, что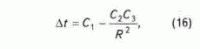
причем
C1, C2, C3 — постоянные величины.Полученное выражение показывает, что вариации интервального времени прохождения сейсмической волны в водозаполненной пористой среде обусловлены изменением усредненной величины радиусов поровых каналов или косвенно проницаемостью такой среды. Это дает основание искать эмпирическую связь между названными показателями как физически оправданную и имеющую выражение в виде формулы
(16).В заключение представляется важным проанализировать физический смысл формулы
(11) с учетом выражения для начального градиента, представленного уравнением (15). Из нее видно, что при достаточно низком начальном градиенте фильтрации, характерном для пород с относительно высокой проницаемостью, как это следует из (15), формула (11) вырождается в зависимость (5) или тождественную ей (1). Другими словами, при достаточно высокой проницаемости традиционные представления о зависимости интервального времени только от пористости породы достаточно справедливы; вернее, зависимостью этого показателя от проницаемости 'можно пренебречь без заметного ущерба для точности оценок.Напротив, при весьма низкой проницаемости в соответствии с формулой (5) начальный градиент фильтрации становится соразмерным градиенту напора, вызванному сейсмическим возбуждением, и при
jq = J второй член двучлена (11) обращается в нуль. Физически это означает, что поровый флюид жестко связан стенками пор и, следовательно, по деформационным характеристикам и агрегатному состоянию приближается к свойствам твердого тела, т.е. становится квазижестким. В такой ситуации пористость, фигурирующая в качестве слагаемого в первом члене выражения (11), становится "равной" нулю или мало от него отличной. Тогда формула (11) вырождается в соотношение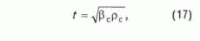
характерное для интервального времени прохождения сейсмической волны в собственно скелете породы, что типично для глинистых разностей. Во всех остальных случаях зависимость
(16) должна проявляться с той или иной долей контрастности. На самом деле сжимаемость связанной жидкости не равна сжимаемости твердого тела; здесь имеется в виду, что βж << βж0Литература
© А.Г.Арье, 1998
It is generally accepted that seismic velocity propagation in fluid-saturated porous media (for example, terrigenous sediments) is a function of their porosity and does not depend on filtration characteristics of these media.
Studies show that there are insufficient grounds for such statement when referred to the system: natural reservoir - condensed fluid (oil or water).
For deposits with good permeability, traditional ideas are proved to be correct with a negligible error. In comparatively low permeable rocks containing large volumes of associated fluid, seismic velocity, among other things, depends on permeability.
A possibility to use the above conditions for estimating rocks permeability by the values of interval time being measured while passing the artificial seismic stimulation through the rock massif is discussed.