|
УДК 001.57:553.98 |
|
|
|
© Э. Багиров, И. Лерч, 1998 |
ВЕРОЯТНОСТНЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ БАССЕЙНОВОГО МОДЕЛИРОВАНИЯ
Э. Багиров, И. Лерч (Университет Южной Каролины)
Успешность проведения поисково-разведочных работ зависит не только от качества и количества геологической, геофизической и геохимической информации, но и от методов обработки и использования этих данных. На сегодняшний день один из наиболее эффективных методов прогноза - воссоздание истории геологического развития бассейна, связанной с процессами генерации, миграции и аккумуляции УВ. В соответствии с этим методом строятся различные компьютерные модели развития бассейна. На основе имеющихся геолого-геофизических данных и геохимических показателей эти модели воссоздают процессы седиментации, палеотермобарические условия в осадочных комплексах и описывают процессы, связанные с преобразованием в этих условиях ОВ в УВ с последующей их миграцией в места скоплений. Математические уравнения, лежащие в основе этих моделей, описывают реальные физические процессы, протекающие в бассейне, а использование современной компьютерной техники позволяет учитывать максимально большее число факторов, влияющих на эти процессы. Вместе с тем процессы и явления, происходящие в земной коре и, в частности, в осадочном чехле, слишком сложны и многогранны, чтобы точно и аккуратно быть описанными математическими формулами и моделями. В то же время независимо оттого, насколько точно модель описывает процесс, результаты любого моделирования зависят от задаваемых входных величин и параметров. Здесь нужно условно различать два типа входных параметров.
Первый тип параметров характеризует непосредственно район исследования. К таким параметрам относятся возраст и глубина залегания стратиграфических комплексов; глубина несогласий и мощность эрозии; геометрия, положение и амплитуда смещения разломов; вещественный состав пород; тип и количество ОВ; современные и палеотепловые потоки и поверхностные температуры; палеобатиметрия; движение фундамента и др. В одномерном бассейновом моделировании все эти переменные задаются в исследуемой точке, в то время как в двухмерном моделировании они определяются в различных точках вдоль линии профиля. Однако очень трудно и, как правило, невозможно однозначно и точно определить значения этих параметров в заданных точках. Дисперсия геологических параметров обусловлена как ошибками измерений, так и случайной природой геологической неоднородности.
Другой тип входных переменных - это параметры, описывающие динамические тепловые и химические процессы. Они обычно входят в динамические уравнения в виде коэффициентов или играют роль начальных и краевых условий. Эти параметры (плотность осадков и флюидов, взаимная растворимость флюидов, теплопроводность матрицы пород, энергия активации и генерационный потенциал керогена и др.), как правило, не привязываются к какому-либо конкретному региону, а являются общими характеристиками процесса в целом. Но, естественно, и эти параметры имеют неопределенность в своих значениях, т.е. не могут быть однозначно заданы некоторым конкретным значением.
Тем самым неопределенность входных параметров обусловливает неопределенность выходных параметров модели, таких как давление, температура, зрелость ОВ, скорости генерации и миграции УВ, их содержание в осадочных комплексах в растворенном и свободном состоянии. Таким образом, задача заключается в выявлении степени этой неопределенности.
Согласно определению модели геологического пространства [1] изменчивость каждого параметра в геологическом пространстве может быть описана некоторым случайным полем. Тогда в каждой пространственно-временной точке изучаемая переменная может быть описана случайной величиной. Таким образом, оценив распределение этой случайной величины, можно, во-первых, в каждой точке определить степень неопределенности данного параметра и, во-вторых, задать значения исследуемого параметра в вероятностных терминах (кумулятивных вероятностей, доверительных интервалов и т.п.).
В принципе для решения этой задачи может быть применен метод Монте-Карло. Для этого на основе априорных соображений каждый из входных параметров описывается некоторой случайной величиной с известным распределением (равномерным, треугольным, нормальным, логнормальным и т.д.). Затем генерируются случайные числа из этих распределений и модель прогоняется много раз с различными наборами входных параметров, составленными из сгенерированных значений. После этого на основе статистического анализа результатов каждой прогонки оцениваются распределения случайных величин, описывающих различные выходные параметры в каждой точке пространства в отдельные моменты времени. Для простых моделей такой подход приемлем. Однако для моделей, одновременно описывающих различные взаимосвязанные процессы, этот метод оказывается бесполезным. Так, одна реализация двухмерной модели GEOPET-II по линиям профилей в Южно-Каспийской впадине [3,4] на рабочей станции SUN занимает около 30 ч. Следовательно, для решения поставленной задачи (с сотней прогонок) потребуется около года. Кроме того, информация, содержащая результаты моделирования вдоль одного среднего профиля, часто занимает несколько мегабайт внешней памяти. И поэтому хранение такого объема информации по результатам десятков прогонок модели, что необходимо при применении метода Монте-Карло, зачастую проблематично.
Таким образом, возникает задача оценки распределений случайных величин, описывающих значения выходных параметров моделирования в каждой точке пространства в различные временные моменты, по результатам минимального числа реализаций модели. В данной статье предлагается метод решения задачи на основе всего двухкратной прогонки программы. Для решения задачи на распределения параметров накладываются дополнительные условия, которые на практике приемлемы и довольно близки к реальности.
Обозначим через р вектор
входных параметров, которые рассматриваются как случайные и взаимно
независимые. Допустим, что каждый элемент, составляющий этот вектор, имеет
треугольное распределение, определенное тремя значениями параметра: минимально
возможным, максимально возможным и наиболее вероятным (соответственно ![]() ). Обычно на практике
значение каждого геологического показателя можно задать таким образом. Тогда
среднее значение (математическое ожидание) и дисперсию этих параметров можно
определить по правилу Симпсона [2]:
). Обычно на практике
значение каждого геологического показателя можно задать таким образом. Тогда
среднее значение (математическое ожидание) и дисперсию этих параметров можно
определить по правилу Симпсона [2]:
![]()
и
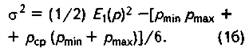
Обозначим через R выходные значения модели. В целом R - это вектор, так как современные бассейновые модели
рассчитывают не одну, а целый набор взаимосвязанных переменных. Не ограничивая
общности, будем рассматривать R как
некоторый отдельно взятый параметр, рассчитываемый моделью (т.е. каждую
выходную характеристику будем оценивать в отдельности). Значения R вычисляются для различных моментов
геологического времени и в каждой точке изучаемого геологического пространства
(например, если это одномерная модель - то вдоль ствола подразумеваемой
скважины, если двухмерная - то в каждой точке профиля и т.д.). Таким образом, R есть функция от
пространственно-временной переменной![]() и от случайного вектора р входных параметров
и от случайного вектора р входных параметров ![]()
![]() . В дальнейшем для простоты изложения
будем записывать ее только как функцию R (р). Однако
надо помнить, что значения этой функции вычисляются во всех точках
. В дальнейшем для простоты изложения
будем записывать ее только как функцию R (р). Однако
надо помнить, что значения этой функции вычисляются во всех точках![]() и
и![]() при реализации модели.
при реализации модели.
Представим каждое значение входных параметров в виде
![]()
где ![]() - случайные отклонения
(флуктуации) от среднего значения
- случайные отклонения
(флуктуации) от среднего значения ![]() при
при![]() Тогда, разлагая
Тогда, разлагая ![]() в ряд Тейлора, имеем
в ряд Тейлора, имеем
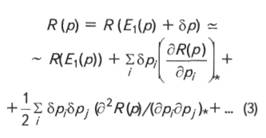
где![]() - значение функции, соответствующее
среднему значению аргумента, т.е. при р = Е1(р) и суммирование идет
по всем входным параметрам. Отсюда следует
- значение функции, соответствующее
среднему значению аргумента, т.е. при р = Е1(р) и суммирование идет
по всем входным параметрам. Отсюда следует
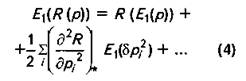
и далее момент второго порядка можно выразить как
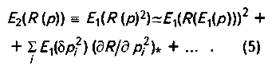
Допустим теперь, что все выходные параметры имеют логнормальное распределение, что близко к действительности. Распределение многих геологических параметров, принимающих только положительные значения, близко к логнормальному. Что касается таких параметров, которые по своей природе не могут быть описаны логнормальным распределением (показатели с ограниченными значениями), то с помощью различных преобразований их также можно свести к логнормальному. Так, пористость меняется от 0 до 1 и поэтому она не может описываться логнормальным распределением, значения которого должны быть положительными и меняться от нуля до бесконечности. Вместе с тем значение пористость/(1 - пористость) вполне соответствует данному условию.
Приведем некоторые условия и свойства логнормальных распределений, которые будут использованы в дальнейшем.
Обозначим через![]() квадратичное отклонение и
квадратичное отклонение и![]() - значение параметра,
соответствующее значению функции распределения
- значение параметра,
соответствующее значению функции распределения![]() (квантиль распределения). Тогда при заданном
(квантиль распределения). Тогда при заданном![]() и медиане
и медиане ![]() функция распределения будет иметь
вид [2]
функция распределения будет иметь
вид [2]
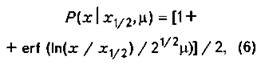
где
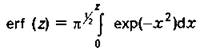
с математическим ожиданием
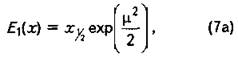
модой
![]()
и дисперсией ![]() ,
равной
,
равной
![]()
Из (7в) следует, что
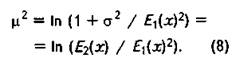
Отметим также, что при ![]()
![]()
![]()
а при ![]() , определенной (16),
, определенной (16),
![]()
Как отмечалось, ![]() соответствует медианному
значению Р = 1/2, в то время как в точке математического ожидания
соответствует медианному
значению Р = 1/2, в то время как в точке математического ожидания ![]()
![]()
Вернемся теперь к численным процедурам. На основании (8) с учетом (4) и (5) имеем:
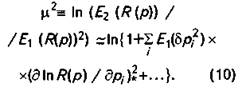
В линейном приближении можно принять
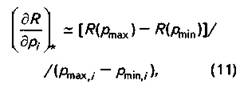
в то время как
![]()
Обозначив
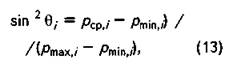
из (1а) и (1б) в
применении к![]() следует
следует
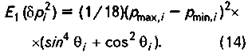
Подставляя (11) и (14) в (10), получим
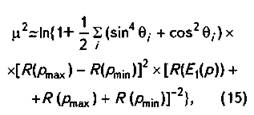
где
![]()
Таким образом, используя (15) и (16), можно оценить среднее значение и дисперсию, которые полностью определяют распределение случайных величин, описывающих данный выходной параметр модели в каждой пространственной точке и различных временных моментах, на основе трех реализаций модели соответственно по минимальным, наиболее вероятным и максимальным данным.
Вместе с тем процедуру
можно еще больше усовершенствовать. Допустим в самом первом приближении, что![]() и
и ![]() представляют собой значения моделируемой
величины, соответствующие 84%-м и 16%-м значениям функции распределения. Тогда
легко показать, что
представляют собой значения моделируемой
величины, соответствующие 84%-м и 16%-м значениям функции распределения. Тогда
легко показать, что
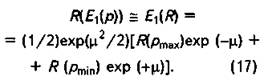
Подставляя (17) в (15),
можно получить итерационную формулу для вычисления ![]() :
:
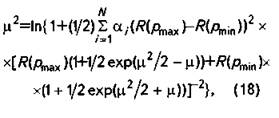
где![]()
Таким путем можно найти оценки распределения множества выходных параметров в каждой пространственной точке, используя результаты только двухкратной реализации модели, что существенно сэкономит компьютерное время.
Численная процедура решения проблемы заключается в следующем:
1. Создаются три входных
файла, содержащих соответственно все минимальные, наиболее вероятные и все
максимально возможные значения параметров. Эти три файла необходимы для
обеспечения соответствующих значений ![]() .
.
2. Программа бассейнового
моделирования прогоняется дважды (один раз с файлом минимально возможных
входных параметров и второй раз - максимально возможных) и создаются два файла
выходных параметров![]() и
и![]() .
.
3.Если в некоторой точке ![]()
![]() , тогда
, тогда![]() в этой точке для заданного параметра принимается
равным нулю. В противном случае в качестве первого приближения
в этой точке для заданного параметра принимается
равным нулю. В противном случае в качестве первого приближения![]() оценивается равным
оценивается равным![]() . Это первое приближение затем
используется в итерационной процедуре, определенной (18), до тех пор, пока не
достигается необходимая степень сходимости.
. Это первое приближение затем
используется в итерационной процедуре, определенной (18), до тех пор, пока не
достигается необходимая степень сходимости.
4. С помощью (17)
оценивается среднее значение![]() , приблизительно соответствующее вероятности Р= 0,68,
а используя (7), (8) и (9), можно вычислить значения параметров (квантили),
соответствующие значениям кумулятивной вероятности (функции распределения) Р=
0,16; 0,5; 0,84. Далее легко найти значения кумулятивных вероятностей для отдельных
значений параметров и наоборот. Дело в том, что если распределение некоторого
параметра в точности подчиняется логнормальному закону, то все точки
, приблизительно соответствующее вероятности Р= 0,68,
а используя (7), (8) и (9), можно вычислить значения параметров (квантили),
соответствующие значениям кумулятивной вероятности (функции распределения) Р=
0,16; 0,5; 0,84. Далее легко найти значения кумулятивных вероятностей для отдельных
значений параметров и наоборот. Дело в том, что если распределение некоторого
параметра в точности подчиняется логнормальному закону, то все точки![]() в интервале значений P от 0,1 до 0,9 будут лежать на одной прямой. На практике
распределение R часто в какой-то
степени отличается от логнормального. Поэтому для ее аппроксимации строим
регрессионную прямую по четырем точкам
в интервале значений P от 0,1 до 0,9 будут лежать на одной прямой. На практике
распределение R часто в какой-то
степени отличается от логнормального. Поэтому для ее аппроксимации строим
регрессионную прямую по четырем точкам ![]() ,
, ![]()
Таким образом, строится функциональная зависимость между значениями параметра в каждой пространственно-временной точке и кумулятивными значениями вероятности, соответствующими этим значениям, причем зависимость достаточно проста, чтобы быстро пересчитывать на компьютере многочисленные варианты.
Для реализации метода были составлены программы SAPAM и RISK2D на языке С для работы на рабочей станции SUN. Программы рассчитаны для вероятностного анализа результатов одномерного и двухмерного бассейнового моделирования GEOPET и GEOPET-II.
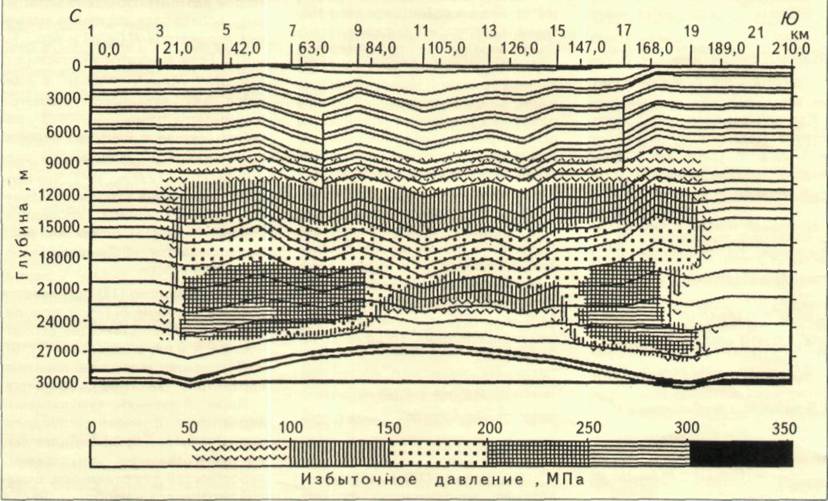
Проиллюстрируем метод на следующих примерах. На рис. 1 показаны прогнозные значения избыточного пластового давления на больших глубинах по результатам бассейнового моделирования в Южно-Каспийской впадине [4] (отсутствие давления на краях профиля и вдоль фундамента объясняется краевым эффектом модели). Наибольшие значения избыточного давления (250-300 МПа) приурочены к глубинным (20-25 км) частям бассейна. Эти высокие значения объясняются преимущественно глинистым составом отложений, затрудняющим отток флюидов. Для использования представленного выше метода были определены границы неопределенности для каждого входного параметра [4]. На рис. 2 представлены значения среднеквадратичных отклонений, характеризующих неопределенность избыточного давления в каждой точке профиля. При сопоставлении рис. 1 и 2 видно, что большие значения неопределенности в моделируемых значениях соответствуют большим значениям давления, т.е. большим глубинам. Это объясняется недостатком информации с этих глубин, и поэтому степень неопределенности входных параметров, относящихся к этим глубинным зонам, гораздо выше, чем в приповерхностной зоне, по которой имеется скважинная информация.
Противоположная картина наблюдается для выходных параметров, связанных с большим числом факторов или процессов. Так, на рис. 3 показаны значения свободного газа в осадочных комплексах. Как видно, основные потенциальные залежи газа приурочены к большим глубинам (свыше 10 км), где концентрации свободного газа могут достигать 20 мг/г породы. В верхней же части разреза лишь местами в продуктивной толще наблюдаются скопления с концентрацией до 8-12 мг/г породы. В целом же концентрации свободного газа здесь незначительны. Если же обратиться к неопределенности (рис. 4), то именно в этой относительно неглубокой зоне она максимальна. Значения соответствующих среднеквадратичных отклонений в плиоценовых и четвертичных отложениях местами превышают 2,4 и почти повсеместно 1,6, в то время как на глубине 10-25 км эти значения, как правило, находятся в пределах 0,8-1,6 при относительно больших значениях самого параметра. Это объясняется тем, что концентрация газа как выходной параметр модели зависит от многих параметров и факторов. И поскольку газ в основном генерируется на больших глубинах, а затем мигрирует вверх по разрезу, то неопределенность в значениях искомого параметра на меньших глубинах включает в себя неопределенность в значениях концентрации газа в глубинной части плюс неопределенность в пропускных свойствах вышележащих комплексов. Таким образом, неопределенность как бы кумулируется вверх по разрезу. Большой эффект здесь, по-видимому, накладывают два хорошо прослеживающихся на сейсмических временных разрезах разлома. Не имея никакой информации о проводящих способностях этих разломов, при построениях модели использовали критические значения для проницаемости этих разломов: в одном случае предполагалось, что разлом непроводящий, а в другом - с высокой (несколько микрометров) проницаемостью. Естественно, что это наложило свой отпечаток на значения неопределенности в содержании свободного газа в вышележащих комплексах.
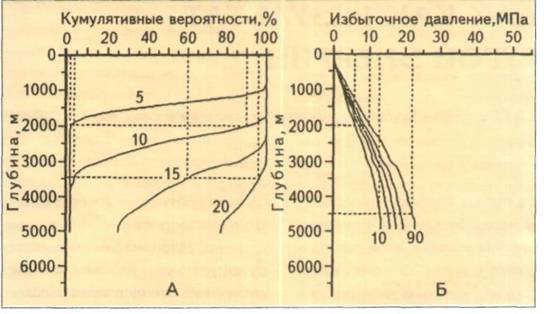
Покажем теперь результаты одномерного моделирования в вероятностных терминах для одной из площадей в Северном море. На рис. 5, А показаны значения избыточного давления в виде изолиний, соответствующие значениям кумулятивных вероятностей. Так, на глубине 3,5 км в точке, для которой строилась модель, избыточное давление не превышает 10 МПа с 5%-й вероятностью, 15 МПа с вероятностью 60 % и 20 МПа с вероятностью 95 %. Аналогично на глубине 2 км с вероятностью 2 % избыточное давление будет меньше 5 МПа и с вероятностью 90 % не превысит 10 МПа. Следовательно, на этой глубине избыточное пластовое давление окажется в интервале 5-10 МПа с вероятностью, близкой к 90 %.
Эти же результаты можно представить в другом виде. На рис. 5, Б представлены значения кумулятивных вероятностей в виде изолиний, соответствующие значениям избыточных давлений.
Подобный анализ можно проводить и для результатов двухмерного моделирования, только для визуализации полученных результатов понадобится большее число рисунков. В первом случае нужно строить профили с изолиниями значений изучаемых параметров, которые не могут быть превышенными с заданной вероятностью, а во втором случае - изолинии вероятностей для конкретных значений параметров. Оба результата одинаково важны. Так, если при бурении скважин буровику нужна от геолога информация о значениях пластового давления, которые не могут быть превышены в различных точках и на разных глубинах с большой (скажем, 90%-й) вероятностью, то экономисту большей степени для решения практических задач.
Метод был апробирован на ряде тестовых и реальных бассейновых моделей [3,4]. В целом же метод может быть применен для любых динамических моделей, особенно таких, реализация которых требует большого объема компьютерного времени. Используя его, можно оценивать степень ошибки, с которой предоставляется тот или иной результат моделирования.
Работа проводилась при содействии Ассоциации финансовой поддержки группы бассейнового моделирования Университета Южной Каролины.
Литература
1. Багиров Э.Б. Определение геологического пространства как основа формализации геологических задач// Геология и геофизика. - 1992. -№ 1. - С. 6-9.
2. Bharucha-Reid A.T. Probabilistic methods in applied mathematics. - New York: Academic Press.
3. Evolution of the South Caspian Basin: geological risks and probable hazards / I. Lerche, E. Bagirov, R. Nadirov, M. Tagiyev, I. Guliyev. - Baku: Nafta-press, 1996.
4. South Caspian Basin: stratigraphy, geochemistry and risk analysis / I. Lerche, A. AIi-zadeh, I. Guliyev, E. Bagirov. - Baku: Nafta-press, 1997.
The results of any simulation of basin development include uncertainty in their values caused by the uncertainty of input data, and these uncertainties are then carried through to all behaviours at all spatial and temporal locations. Therefore it is appropriate to present the results of modelling in probabilistic terms. Applying the Monte Carlo method is a problem for most basin models because of the large amount of computer time required for each run of the model and also because of the storage space requirements for outputs from many runs from which to construct the probabilistic output results.
A numerical procedure for estimation of the output probability distribution (for as many outputs as one is interested in) is given here for all time-steps and at all spatial points of a basin model calculation. The method is surprisingly accurate and uses results of only two runs of the model, although accuracy can be also improved with three or more runs, of course. The computer time saved is more than adequate justification for the use of the approximate method, as is the fact that the ranges of uncertainty and underlying distributions of input parameters are not too well known either, thereby justifying further the use of an approximate, quick, and both labor and time-saving method. The values of logarithmic standard deviation around each mean are used as measures of uncertainty of predicted parameters, and the presentation of results in probabilistic terms is an enormous aid to assessing more accurately the relevant risk analysis for all quantities, ranging from overpressure likelihood through to reservoir characterization and to hydrocarbon finding probabilities.
Рис. 1. ЗНАЧЕНИЯ ИЗБЫТОЧНОГО ДАВЛЕНИЯ ВДОЛЬ ЛИНИИ ПРОФИЛЯ СЕВЕР - ЮГ В ЮЖНО-КАСПИЙСКОЙ ВПАДИНЕ
![]() Рис. 2. ЗНАЧЕНИЯ СРЕДНЕКВАДРАТИЧНЫХ ОТКЛОНЕНИЙ
ДЛЯ ИЗБЫТОЧНОГО ДАВЛЕНИЯ ВДОЛЬ ЛИНИИ ПРОФИЛЯ В ЮЖНО-КАСПИЙСКОЙ ВПАДИНЕ
Рис. 2. ЗНАЧЕНИЯ СРЕДНЕКВАДРАТИЧНЫХ ОТКЛОНЕНИЙ
ДЛЯ ИЗБЫТОЧНОГО ДАВЛЕНИЯ ВДОЛЬ ЛИНИИ ПРОФИЛЯ В ЮЖНО-КАСПИЙСКОЙ ВПАДИНЕ
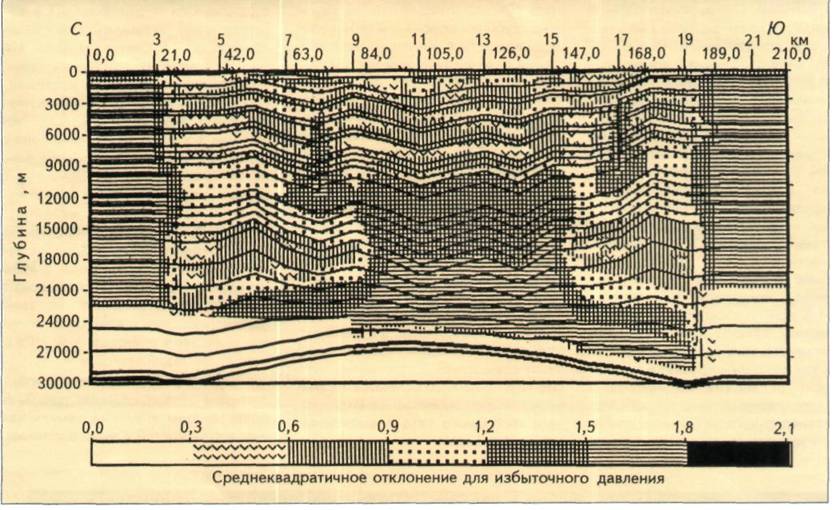
Рис. 3. ЗНАЧЕНИЯ КОНЦЕНТРАЦИЙ СВОБОДНОГО ГАЗА ВДОЛЬ ЛИНИИ ПРОФИЛЯ В ЮЖНО-КАСПИЙСКОЙ ВПАДИНЕ
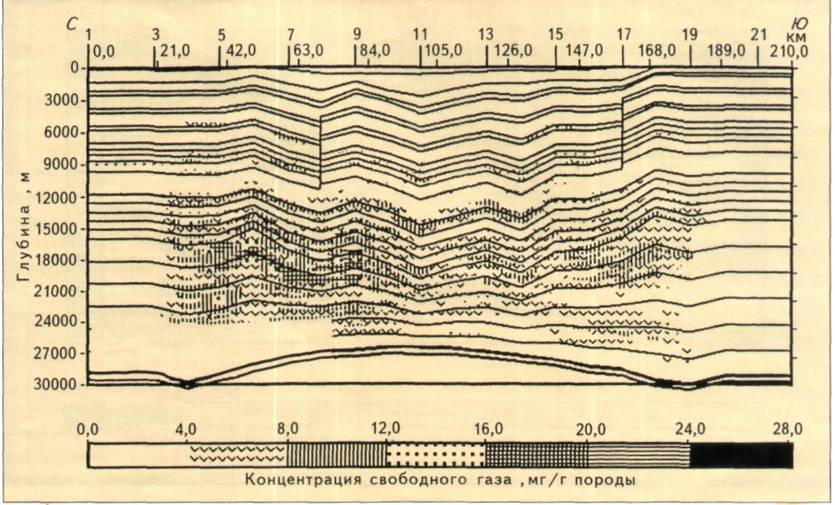
Рис. 4. ЗНАЧЕНИЯ СРЕДНЕКВАДРАТИЧНЫХ ОТКЛОНЕНИИ ДЛЯ КОНЦЕНТРАЦИИ СВОБОДНОГО ГАЗА ВДОЛЬ ЛИНИИ ПРОФИЛЯ В ЮЖНО-КАСПИЙСКОЙ ВПАДИНЕ
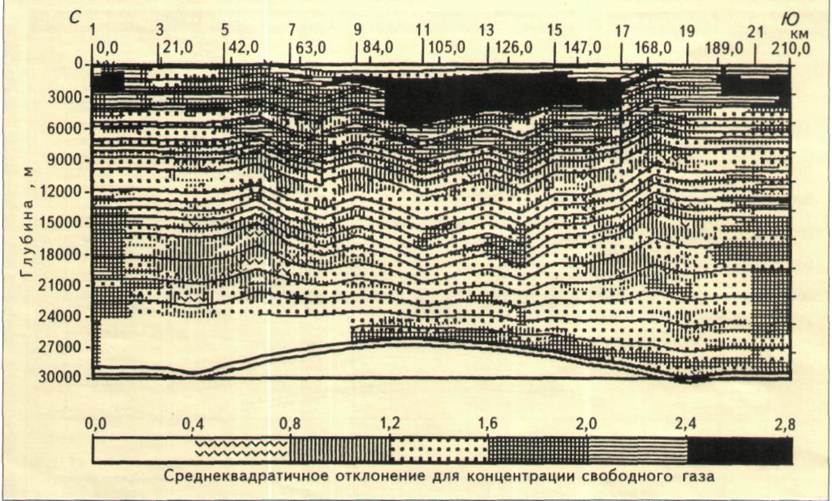
Рис. 5. ИЗМЕНЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ИЗБЫТОЧНОГО ДАВЛЕНИЯ (А) И КУМУЛЯТИВНЫХ ВЕРОЯТНОСТЕЙ (Б) С ГЛУБИНОЙ