К оглавлению

УДК 550.34.01

 

© Г.В. Ларин, В.В. Попов, 1998

ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ НА ОСНОВЕ ПОСЛОЙНОГО МИГРАЦИОННОГО ПРЕОБРАЗОВАНИЯ

Г.В. Ларин, В.В. Попов (ВНИИгеофизика)

При структурных построениях в условиях сложного геологического строения среды и значительных глубин исследования возрастает роль выбора адекватного алгоритма миграции и точности задания скоростной модели. Говоря о выборе алгоритма, мы имеем в виду необходимость проведения миграции по исходным сейсмограммам, причем с учетом преломления волн на промежуточных преломляющих границах. Если же говорить о скоростных параметрах, то их погрешности в случае больших и резко меняющихся углов наклона горизонтов, при наличии рассеивающих границ и дифрагирующих объектов приводят к неправильному сносу элементов разреза на плоскости изображения, не обеспечивают фокусировку дифрагированных волн и т.п. Иными словами, скоростные погрешности приводят к искажению кинематической и динамической картины на результирующем разрезе. Вместе с тем представления о скоростном строении среды в значительной мере формируются в результате проведения разновременного анализа по методу ОГТ и построения на его основе вертикальных и/или горизонтальных спектров скоростей. Однако полученные в этом случае скоростные зависимости при достаточно сложном строении среды могут иметь значительные погрешности. Основная причина их появления связана со структурными факторами: эффективные скорости зависят от угла наклона и кривизны отражающих горизонтов и поэтому не описывают реального распределения скоростей распространения сейсмических волн.

Для снижения трудностей, возникающих на этапе определения скоростей, можно применить альтернативный методу ОГТ подход, поскольку данные многократного профилирования в силу избыточности регистрируемой информации в принципе достаточны для определения скорости распространения сейсмических волн. Отличия скоростей, используемых при миграционных преобразованиях первичных сейсмограмм (миграции до накапливания по ОГТ), от реального распределения скоростей в среде оказывают достаточно значительное влияние на форму получаемого изображения среды. Поэтому имеется возможность осуществлять скоростной анализ на основе миграционного преобразования исходных сейсмограмм, где суммирование производится не вдоль годографа ОГТ, а вдоль годографа дифракции. Определяемые на основе такого подхода скорости в отличие от разновременного анализа сейсмограмм ОГТ не содержат искажений, связанных со структурным фактором - наклоном и кривизной отражающих границ.

Оптимальным графом обработки сейсмических данных в сложных условиях представляется следующий. Полевые сейсмограммы после предварительной обработки до суммирования обрабатываются программой анализа миграционных скоростей с получением скоростного разреза в первом приближении. Далее с полученными скоростными значениями проводится среднескоростная миграция исходных сейсмограмм до суммирования. По результирующему глубинному разрезу выделяется первая сильно преломляющая граница и проводится вторичный анализ скоростей с учетом преломления волн на этой границе. После получения уточненных значений скорости (ниже преломляющей границы) осуществляются миграция исходных сейсмограмм с учетом преломления и построение уточненного глубинного динамического разреза. При наличии еще одной сильно преломляющей границы процесс может быть повторен. Таким образом, последовательное сочетание процедур анализа скоростей и миграции до накапливания позволяет единообразно и последовательно решать задачи определения пластовой скоростной модели и построения мигрированного глубинного разреза с компенсацией эффекта преломления волн на промежуточных границах раздела.

Основой скоростного анализа являются процедура миграции сейсмограмм равных удалений [2, 3] и построение динамического изображения среды вдоль заданной в некоторой точке профиля вертикали. Критерий выбора оптимальной скорости базируется на свойстве динамической неустойчивости миграции исходных сейсмограмм к погрешностям скорости. Суть метода состоит в следующем. Исходные трассы группируются по признаку равных удалений l, и таким образом получается набор разрезов равноудаленных трасс. Выбрав на профиле вертикаль X, вдоль которой необходимо определить скорость V(X, Z) (или V(X, t), и задаваясь набором скоростных законов, можно осуществлять миграцию на выбранную вертикаль каждого созданного разреза равноудаленных трасс с различными скоростными зависимостями из указанного набора. Результаты миграции каждого разреза с одним и тем же скоростным законом (вертикальные сейсмограммы) группируются. В тех случаях, когда принятая для миграционного преобразования скорость соответствует распределению скорости в среде, сигналы продолженной волны на сгруппированных указанным образом вертикалях будут располагаться вдоль прямой Z = const (или вдоль прямой t = const, если результативные трассы получать в масштабе вертикального времени). В случае несоответствия скорости преобразования и скорости в среде сигналы на вертикальных сейсмограммах, сформированные при миграции различных разрезов, будут все более отклоняться от прямой Z = const (t= const) по мере возрастания абсолютного значения удаления. Если скорость, принятая для миграции, занижена по отношению к скорости в среде, то изображение точек дифракции и отражающих границ на плоскости (Z, l) (или (t, l) обращено выпуклостью вниз. При завышении миграционной скорости изображение объектов обращено выпуклостью вверх.

Вертикальные сейсмограммы позволяют построить аналог вертикального спектра скоростей, поэтому решение по выбору оптимальной скорости можно принимать, анализируя два изображения: вертикальные сейсмограммы и аналог вертикального спектра скоростей. Исходя из поведения осей синфазности отраженных и/или дифрагированных волн в плоскости вертикальных сейсмограмм выбирается та скорость, при которой сигналы продолженной волны наиболее близко располагаются вдоль горизонтальной линии Z=const (t=const). В плоскости аналога вертикального спектра оптимальные скорости будут соответствовать распределению экстремальных значений энергии. Осуществление подобной процедуры на нескольких вертикалях профиля позволяет путем интерполяции полученных скоростных законов построить распределение скоростей распространения волн для всего профиля.

Естественно, наличие в среде резких преломляющих, криволинейных несогласно залегающих границ приведет к искажениям скоростной модели, получаемой на основе миграции сейсмотрасс равных удалений. Эти искажения обусловливаются неучетом при миграции преломления волн на таких границах. Кроме того, при подобном скоростном анализе предполагается использование сейсмограмм ОПВ, что приводит к снижению разрешающей способности метода при увеличении глубины исследований вследствие ограниченной длины указанных сейсмограмм. Даже при наличии достаточно протяженных сейсмограмм ОПВ, т.е. при увеличенном диапазоне набора удалений, скоростной анализ в сильно неоднородной среде будет осложнен из-за влияния латерального градиента средней скорости.

Для преодоления возникающих затруднений представляются возможными два подхода, основанных на послойном решении задачи. В первом случае на базе анализа изображений, полученных путем миграции разрезов равноудаленных трасс, устанавливается распределение скорости V1 в первом слое, подошвой которого является первая сильно преломляющая граница. Зная эту скорость, можно строить глубинный мигрированный разрез для корреляции этого горизонта. Затем скоростной анализ проводится вновь - для второго слоя: путем миграции разрезов равных удалений и расчетов годографа дифракции с учетом преломления на выделенном горизонте (при уже определенной скорости V1) определяется скорость V2 в этом слое. Далее, на основе пластовой миграции (до или после суммирования по ОГТ) выявляется рельеф второй сильно преломляющей границы. На следующем этапе - при известных значениях скоростей V1, V2 и строении вышележащих границ - аналогичным способом исследуется скорость в третьем слое и т.д.

Разработанная в обрабатывающей системе СЦС-5 на рабочих станциях SUN программа анализа миграционных скоростей VAN реализует алгоритм миграции разрезов равноудаленных трасс в среднескоростном и послойном вариантах. Общий алгоритм заключается в следующем. Трассы исходных сейсмограмм, попадающие в программно-рассчитываемую базу суммирования, выбираются по признаку равных удалений l из заданного набора L удалений, и осуществляется их миграция на заданную вертикаль X исследуемой среды. Миграция производится в пределах интересующего интервала глубин с некоторым задаваемым шагом по глубине, а также со средними или в случае послойного решения задачи интервальными скоростями Vn(X, Z) из набора N скоростных законов. Этот набор определяется следующим образом: задается некоторый базовый скоростной закон V(X, Z), а также максимальное отклонение D от этого закона (%) и шаг отклонений(%). Очередной n-й закон определяется из базового распределения по соотношению

На выходе программы последовательно формируется N вертикальных сейсмограмм, каждая из которых соответствует определенному скоростному закону и содержит по L трасс. Каждая такая трасса представляет собой изображение среды  на одной и той же вертикали Х = const как результат миграции разрезов равноудаленных трасс при заданном скоростном законе. Формирование изображения в точках среды (X, Z) при миграции трасс равных удалений l осуществляется на основе D-преобразования по формуле

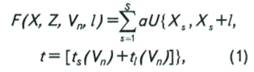
где а - весовые коэффициенты; X- координата анализируемой вертикали; Xs - координата пункта возбуждения; S - число источников, попадающих в базу суммирования; l - расстояние между источником и приемником;и - соответственно времена распространения волн от s-ro пункта возбуждения до точки (X, Z) и от точки (X, Z) до пункта приема Хl , удаленного от Xs на расстояние l.

В случае послойного решения задачи времена рассчитываются с учетом преломления волн на заданных промежуточных границах. Выбор способа анализа осуществляется в зависимости от представления входных параметров. Если в них задана одна или несколько границ, то производится анализ интервальных скоростей на основе миграции с трассированием луча дифрагированной волны. В противном случае (если во входном потоке границы не заданы) производится анализ средних скоростей, т.е. времена ts и tl в соотношении (1) рассчитываются по прямолинейным лучам, соединяющим точку анализа (X,Z) с точками Xs и Xl соответственно.

Второй подход к определению скоростей с компенсацией эффекта преломления волн основан на использовании искусственно формируемых в точках промежуточных границ сейсмотрасс. Идея этого подхода впервые изложена в работе [1] более 20 лет назад, а практически реализована 10 лет спустя в алгоритме послойного быстрого преобразования Кирхгофа (БПК) для временных разрезов (Попов В.В., 1988; Ларин Г.В., Попов В.В., 1990). Формирование промежуточных трасс производится после каждого последовательного определения скорости в некотором слое и положения преломляющего горизонта, являющегося его подошвой. Это позволяет снять искажающее влияние вышележащей толщи и перейти к изучению скорости в очередном слое. Иными словами, если предположить, что колебаниявозбуждаются источниками и регистрируются приемниками в дискретном множестве точек некоторой промежуточной границы G, то для анализа скорости путем миграции равноудаленных трасс ниже этой границы можно вместо сейсмотрасс  , зарегистрированных на дневной поверхности, использовать сейсмотрассы .

Естественно, практически осуществимым является не расстановка источников и сейсмоприемников на промежуточных границах, а расчет эффективных сейсмотрасс . Скоростные параметры слоя, покрывающего границу G, и конфигурация этой границы считаются известными (они могут быть определены, допустим, изложенным выше методом).

Пересчет сейсмического поля с дневной поверхности на промежуточную границу осуществляется в два этапа. Сначала в пределах каждой сеймограммы ОПВ производится пересчет на промежуточную границу сейсмоприемников по соотношению

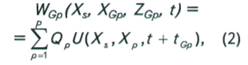
где Qр - весовые коэффициенты; Р - число пунктов приема, в которых зарегистрированы колебания, порождаемые s-м источником;  - время распространения волны от точки расположения приемника на промежуточной границе до приемников Хр на дневной поверхности, относящихся к данному пункту возбуждения Xs.

Затем полученные трассы сортируются по общему пункту приема и в пределах каждой сейсмограммы ОПП производится пересчет на промежуточную границу источников колебаний с использованием следующего соотношения:

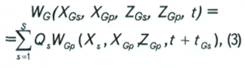
где Qs - весовые коэффициенты; S - число пунктов возбуждения, относящихся к данной сейсмограмме ОПП;- время распространения волны от точкирасположения источника на промежуточной границе до источников Xs на дневной поверхности, относящихся к данному пункту приема .

Полученные эффективные трассы используются для анализа скорости толщи, лежащей под горизонтом G, путем их выборки по признаку равных удалений и построения вертикальных сейсмограмм. При этом применяется соотношение (1), в которое вместо трасс U(t) подставляются трассы. Пересчет волнового поля с горизонта G на следующую границу осуществляется по тем же формулам (2) и (3), в которых вместо зарегистрированных на дневной поверхности сейсмограмм U используются эффективные сейсмограммы WG. Конечно, число подобных пересчетов ограничено из-за нарастания шумов преобразований. Вместе с тем этот способ в ряде случаев может оказаться предпочтительнее за счет повышения разрешающей способности вследствие "погружения" системы сейсмограмм ОПВ и уменьшения мощности перекрывающей толщи над слоем, в котором анализируется скорость. Кроме того, здесь проще учитывать латеральный градиент скорости. Представляется, что может оказаться полезным сочетание двух описанных способов.

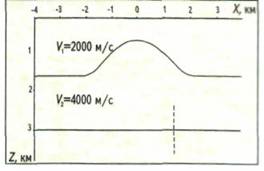
Опробование программы VAN проводилось по Modele de Vitesse, схематически изображенной на рис. 1. Фрагмент волнового поля для фланговой системы наблюдений с максимальным удалением -2575 м, выносом -200 м показан на рис. 2. Расстояние как между пунктами возбуждения, так и пунктами приема составляло 50 м. Анализ скоростей проводился на вертикали с координатой X= 3000 м.

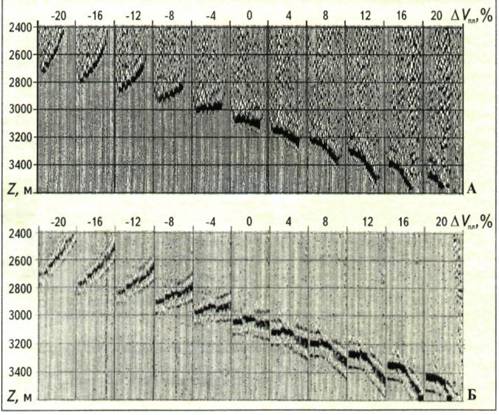
Поскольку скоростная характеристика обрабатываемой модели была абсолютно неизвестна, то был предложен следующий подход к решению задачи. На первом этапе выбирается произвольный базовый скоростной закон и осуществляется анализ при скоростных распределениях в широком диапазоне отклонений от него. Это позволяет получить начальное представление о скоростном строении среды и определить направление дальнейшего уточнения параметров модели. В данном примере был использован набор из девяти скоростных законов, максимально отклоняющихся от базового на ±20 % с шагом 5 % (рис. 3, А). Следовательно, результатом работы программы является девять групп трасс (по 48 трасс в каждой группе), соответствующих этим девяти законам скорости (рис. 4, A). Каждая трасса в группе является изображением среды на вертикали X= 3000 м. На этих изображениях выделяются оси синфазности, близкие к горизонтальным линиям, по глубине расположения которых на соответствующих графиках из набора скоростей определяется скорость искомого закона. К примеру, одна из таких осей расположена на глубине 600 м и соответствует кривой, отличающейся от опорного закона на 5 % (т.е. V(600 м) = 1680 м/с). Другая горизонтальная ось, которая получена при скорости, отклоняющейся от базовой на 10 % (V= 1760 м/с), находится на глубине 900 м и т.д. Таким образом, на первом этапе применения программы получена кривая V(Z), пересекающая заданный набор скоростных зависимостей (см. жирную кривую на рис. 3, А) и дающая начальное представление о скоростной характеристике среды на заданной вертикали. Она служит основой для второго этапа - уточнения этой характеристики. На втором этапе использовался также набор из девяти законов скоростей, но с меньшим максимальным отличием (до ±8 %) от исходного распределения, полученного на первом этапе, при шаге 2 % (см. рис. 3, Б). Для каждого закона из нового набора сформирована группа трасс в плоскости изображений (Z, l) (см. рис. 4, Б) и по выделенным горизонтальным осям синфазности построен уточненный закон (см. жирную линию на рис. 3, Б). Полученная скоростная кривая является оптимальной для миграции и гораздо лучше соответствует средней скорости, чем скорости, определенные по методике ОГТ. На ее основе по элементарной формуле была построена зависимость пластовой скорости от глубины Vпл(Z) (см. рис. 3,б).

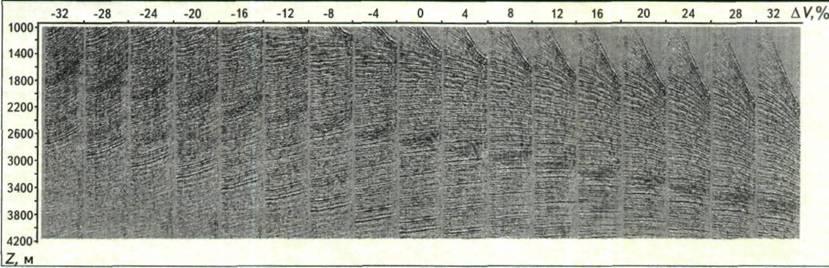
Рис. 5, рис. 6, рис. 7, полученные с помощью программы VAN, демонстрируют пример ее применения на полевом материале. Исходные сейсмограммы ОГТ по одному из профилей Западной Сибири изображены на рис. 5.

Поскольку данные о скоростях отсутствовали, то в качестве базового скоростного закона была принята постоянная скорость 2500 м/с, а сканирование скоростей проводилось в диапазоне отклонений ±32 % от базовой скорости с шагом 4 %.

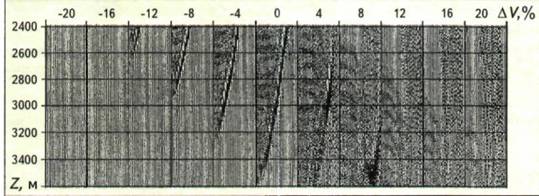
Интервал удалений, включенных в обработку, составил 700-2900 м. Рассчитанный аналог вертикального спектра скоростей для координаты -1500 м представлен на рис. 6. С помощью "автопикинга" скоростного спектра получена скоростная кривая, оптимальная для миграции исходных сейсмограмм. Вертикальные сейсмограммы, которые программа позволяет получать по желанию пользователя для визуального анализа, представлены на рис. 7.

Как отмечалось, в достаточно сложных условиях проведение скоростного анализа (а равно и миграции до суммирования) без учета преломления не может привести к положительным результатам. Это положение иллюстрируется рис. 8-10. На рис. 8 изображена модель среды, имитирующая соляно-купольную тектонику. Пунктирной линией показан отрезок вертикали, вдоль которого проводился скоростной анализ. Рис. 9, на котором приведен результат среднескоростного анализа, показывает, что даже при задании истинной средней скорости изображение нижней отражающей границы в плоскости вертикальных сейсмограмм разрушено, вследствие чего также произойдут расфокусировка сигналов и разрушение изображения границы при миграции.

Причиной разрушения является неучет преломления волн на верхней криволинейной границе с резким перепадом скоростей. Подтверждением этому служит рис. 10, на котором изображены результаты скоростного миграционного анализа с учетом преломления. Первый результат (см. рис. 10, A) получен путем трассирования лучей, второй - путем пересчета исходных трасс на криволинейную границу (см. рис. 10, б). В обоих случаях мы видим достаточно четкое изображение нижней отражающей границы, конфигурация которой в ряду вертикальных сейсмограмм близка к горизонтальной линии как раз при истинном значении скорости. Отсюда следует, что и миграция с учетом преломления даст правильное изображение границы в данной точке профиля.

Таким образом, можно сделать следующие выводы. В сложных сейсмогеологических условиях необходим переход от миграции временных разрезов к миграции исходных сейсмограмм. Для эффективного использования процедуры миграции следует предварительно проводить определение миграционных скоростей. Причем для получения максимально достоверной картины глубинного (мигрированного) разреза скоростной анализ в рамках среднескоростной модели среды недостаточен, так как приводит к значительным искажениям, а в некоторых случаях и разрушению изображения среды. Требуется определять скорости на основе послойного миграционного преобразования, которое возможно проводить двумя способами: первый - на основе трассирования лучей между точками среды и источниками и приемниками на дневной поверхности; второй - путем пересчета (погружения) исходного волнового поля на преломляющие границы. Определение достоинств и недостатков каждого из способов требует дальнейших исследований и экспериментального опробования с привлечением большого объема полевых материалов. Мы полагаем, что на практике будет полезным сочетание обоих подходов как к построению динамических глубинных разрезов, так и к определению скоростей на основе миграции.

Литература

1.      Васильев С.А., Матвеенко Г.В., Урупов А.К. Алгоритмы компенсации искажений сейсмических изображений, обусловленных наличием криволинейных промежуточных сильно преломляющих границ // Прикладная геофизика. - М., 1976. - Вып. 84. -С.8-20.

2.      Мешбей В.И., Лангман С.Л., Богданов Г.А. Итеративная пластовая миграция сейсмограмм отраженных волн //Прикладная геофизика. - М., 1985. - Вып. 111. - С.8-20.

3.      Тимошин Ю.В. Импульсная сейсмическая голография. - М.: Недра, 1978.

Abstract

Consideration is being given to a way of determining seismic waves velocities under complicated geological structure conditions based on travel conversion of equal-spaced seismic records. Velocities determined unlike velocity analysis by CDP method don't contain distortions associated with a structural factor - dipping and curving of reflection limits.

Model material shows that with sharp refracting curved boundaries in the medium a travel velocity analysis as well a travel of initial seismic records within the limits of averaged velocity model could not provide positive results. This will require a transition to inlayers decision of the task based on the successive combination of procedures of velocity analysis and original seismic records travel with regard to wave refraction at intermediate boundaries. Two algorithms for effective solving this task are proposed. One is based on ray path between points of the medium and sources and receivers located on the day surface, and the another - on original wave field being converted into intermediate reflecting boundaries.

 

Рис. 1. МОДЕЛЬ СРЕДЫ

 

Рис. 2. СЕЙСМОГРАММЫ ОПВ

 

Рис. 3. ПЕРВЫЙ (А) И ВТОРОЙ (Б) ВАРИАНТЫ НАБОРА СКОРОСТЕЙ

 

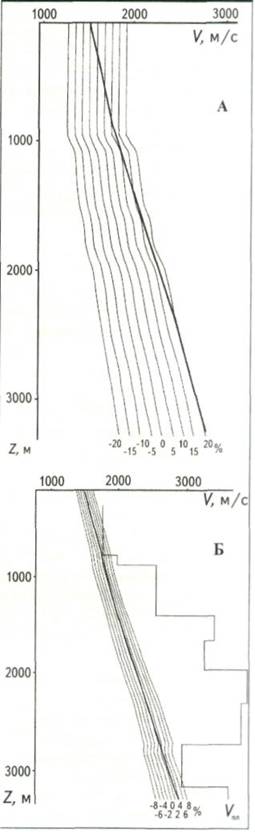
Рис. 4. ВЕРТИКАЛЬНЫЕ СЕЙСМОГРАММЫ, ПОЛУЧЕННЫЕ НА ПЕРВОМ (А) И ВТОРОМ (Б) ЭТАПАХ АНАЛИЗА

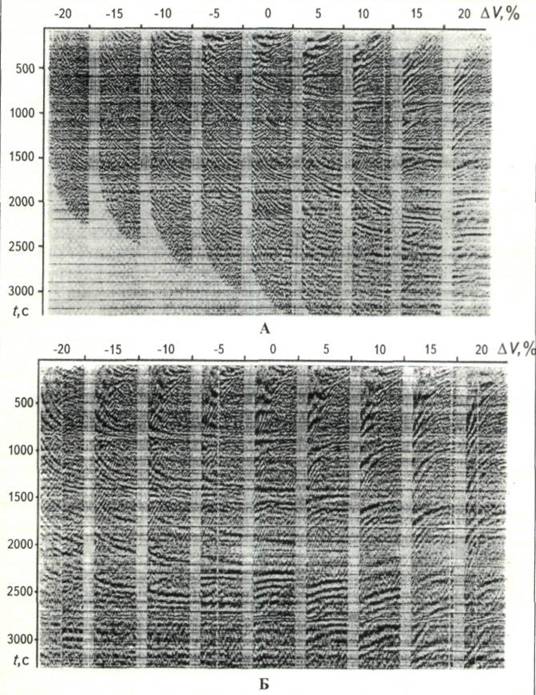
Рис. 5. ФРАГМЕНТ ПРОФИЛЯ ИСХОДНЫХ СЕЙСМОГРАММ (Западная Сибирь)

 

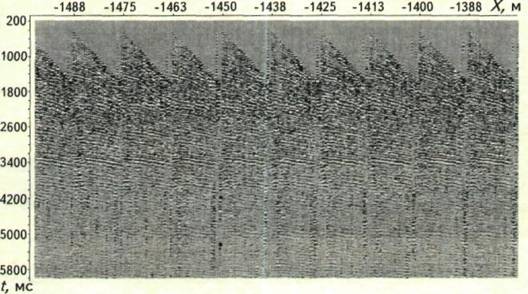
Рис. 6. АНАЛОГ ВЕРТИКАЛЬНОГО СПЕКТРА СКОРОСТЕЙ

 

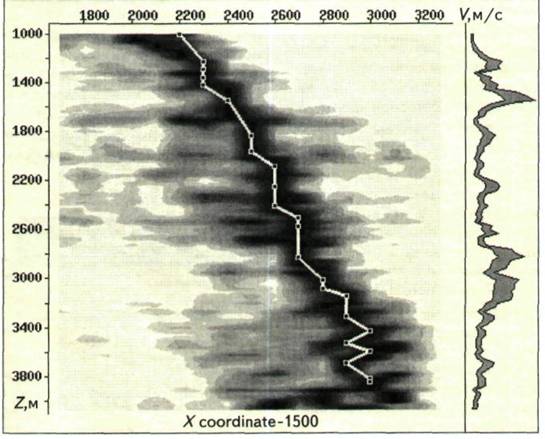
Рис. 7. РЯД ВЕРТИКАЛЬНЫХ СЕЙСМОГРАММ (базовая скорость 2500 м/с)

 

Рис. 8. МОДЕЛЬ СРЕДЫ, ИМИТИРУЮЩАЯ СОЛЯНО-КУПОЛЬНУЮ ТЕКТОНИКУ

 

Рис. 9. РЕЗУЛЬТАТ СРЕДНЕСКОРОСТНОГО АНАЛИЗА

 

Рис. 10. ВЕРТИКАЛЬНЫЕ СЕЙСМОГРАММЫ, ПОЛУЧЕННЫЕ С УЧЕТОМ ПРЕЛОМЛЕНИЯ ВОЛН ПУТЕМ ТРАССИРОВАНИЯ ЛУЧЕЙ (А) И ПЕРЕСЧЕТА ИСХОДНЫХ ТРАСС НА ПРОМЕЖУТОЧНУЮ КРИВОЛИНЕЙНУЮ ГРАНИЦУ (Б)