|
УДК 519:550.8:553.98 |
© В.М. Валиев,1999 |
СТОХАСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ОСВОЕНИЯ УГЛЕВОДОРОДНЫХ РЕСУРСОВ
В.М.Валиев (ИПГНГМ АН Азербайджана)
Геологогеофизические работы по своему характеру являются начальным этапом освоения УВ-ресурсов. На этом этапе получают необходимую предварительную информацию, используемую для правильного выбора направлений работ при разведке и разработке новых нефтеносных объектов. Очевидно, что качественное проведение геофизических работ позволяет повысить эффективность поисково-разведочных работ и существенно снизить затраты на их проведение.
Для правильной количественной и качественной оценки характера проведения геолого-геофизических работ, а также для определения аналитического выражения их влияния на поисково-разведочные работы и разработку введем понятие "степень подготовленности перспективных структур" и обозначим эту величину u. Эта величина нормируется и характеризует объем проведенных в регионе геолого-геофизических работ, т.е. u
О [0,1]. Ее значения можно определить разными способами, причем значение u, равное 0, соответствует случаю, когда в регионе не были проведены никакие геофизические работы, а значение u, равное 1, – когда в регионе были проведены геофизические работы в большом объеме (теоретически в бесконечном объеме).Ясно, что значение u зависит от объема информации (х), полученной в результате проведения в
регионе геолого-геофизических работ. Аналитический вид зависимости u от х определяется способом получения этой информации. При этом максимальное и минимальное значения u будут разными для различных способов. Последнее означает, что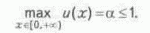
Отметим, что первая производная
u(х) положительная и является монотонно убывающей функцией u' (x)>0. Например, пусть производная функции u(х) имеет следующий аналитический вид: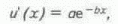
где а и
b некоторые константы, которые зависят, как было отмечено, лишь от способа получения информации. При этом считается, что и(0) =0 и u(Ґ) =a. В этом случае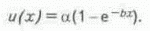
После проведения в регионе некоторого объема геофизических работ начинается поисково-разведочное бурение на перспективных структурах.
Вероятность попадания поисково-разведочной скважины в нефтеносный пласт (р) различна для различных регионов и сильно зависит от качества и объема проведенных геофизических работ. Значит, эта вероятность зависит от степени подготовленности перспективных структур. Аналитически эту вероятность в зависимости от
u можно задать следующим уравнением: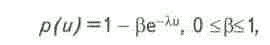
где
b и l – константы, зависящие от способа получения информации.Известно, что для каждого региона с учетом его особенностей даже при значении u=0 вероятность попадания в нефтеносный пласт равна некоторому положительному числу
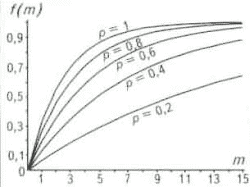
p(0)=p0, р0>0; р(1)=р*, р* < 1 и р* = 1-e. Здесь р0 и e являются достаточно малыми числами. Тогда получаем, что b = 1 - р0, l =ln((1-p*)/(1-p0)) Отсюда вероятность попадания поисково-разведочной скважины в нефтеносный пласт в зависимости от u имеет следующий вид (рис. 1):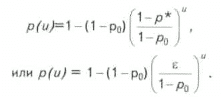
После определения этой вероятности на передний план выходит
проблема "открытия" месторождения. Последнее является относительным понятием и определяет полное открытие месторождения и ввод его в эксплуатацию. С бурением разведочных скважин запасы промышленной категории месторождения уточняются и определенное число скважин обеспечивает полную разведанность месторождения. Таким образом, процесс открытия месторождения в некотором смысле прямо зависит от числа пробуренных поисково-разведочных скважин. В зависимости от объема проведенных в регионе геофизических работ каждая пробуренная поисково-разведочная скважина в свою очередь может попасть или не попасть в нефтеносный пласт. Поэтому можно утверждать, что открытие месторождения зависит не только от числа поисково-разведочных скважин, но и от вероятности попадания в нефтеносный пласт, т.е. от степени подготовленности структур (рис.2).Для уточнения процесса открытия месторождения нужно задать закон его открытия, который можно выразить в следующем виде:

Используя формулу
(1), вероятность открытия месторождений Р(n) можно вычислить с помощью формулы Колмогорова:
Здесь предполагается, что вероятность попадания в нефтеносный пласт пробуренной скважины не зависит от месторождения, а бурение одной скважины не зависит от бурения другой.
Одним из основных путей увеличения добычи нефти является открытие возможно большего числа нефтеносных объектов. В этом случае в качестве показателя эффективности выступает математическое ожидание числа открытых месторождений по каждому региону. Открытие этих месторождений зависит от используемых общих средств, числа скважин и вообще от материальных возможностей организаций, занимающихся подготовкой нефтеносных объектов.
Допустим, что мы имеем некоторые средства для бурения поисково-разведочных скважин, например обладаем возможностью бурения К поисково-разведочных скважин. Принимаем, что распределение пробуренных поисково-разведочных скважин по месторождениям, где ведутся разведочные работы, является детерминированным (это распределение, по всей вероятности, может быть и стохастическим).
Предположим, что имеется определенный объем средств для бурения поисково-разведочных скважин. Примем следующие обозначения:

В этом случае математическое ожидание открытия месторождений из
N подготовленных перспективных структур имеет следующий вид: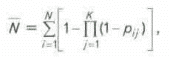
где Pij
– вероятность попадания i-и скважины на j-м месторождении в нефтеносный пласт.Если нефтеносные объекты, где проводят поисково-разведочные работы, однотипны (одинаковые геометрические, геологические особенности и глубина залегания), тогда для каждого объекта будет использовано
K/N скважин и вероятность попадания в нефтеносный пласт для всех месторождений будет одинаковой, т.е. Pij=P. Тогда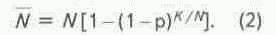
Пример
1. С помощью 12 поисково-разведочных скважин требуется открыть четыре однотипные нефтеносные перспективные структуры. Вероятность попадания в нефтеносный пласт одной скважины равна 0,3. Необходимо найти математическое ожидание числа открытых месторождений.Решение. По формуле (2):
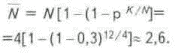
Значит, математическое ожидание числа открытых месторождений
N = 2,6 месторождения.Как отмечалось, распределение перспективных нефтеносных объектов в регионе неравномерно по глубине залегания и размерам (по геометрии площади и объему запасов), маленькие структуры встречаются чаще, с увеличением глубины число структур тоже меняется значительно.
Число перспективных структур региона
N классифицируем по 5 классам в зависимости от интервалов глубины залегания и размеров. Допустим, что К скважин распределены по этим классам детерминированно. Очевидно, что из-за различия геометрических и геологических особенностей перспективных структур, принадлежащих каждому классу, вероятность попадания каждой скважины в нефтеносный пласт будет различной по классам. В связи с этим для открытия нефтяных структур каждого класса требуется разное число поисково-разведочных скважин:N1 + N2 +... + Ns= N;
K1 + K2 +...+ Ks = К,
где Ns, Ks – соответственно число перспективных структур и поисково-разведочных скважин, принадлежащих i-му классу. Тогда математическое ожидание открытия месторождений i-го класса вычисляется аналогично формуле (2):
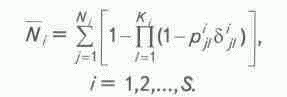
Если по каждому классу перспективных структур вероятности попадания поисково-разведочной скважины в нефтеносный пласт одинаковы, т.е.
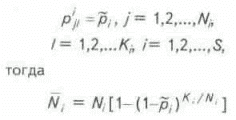
и математическое ожидание открытия месторождений по всем классам вычисляется по формуле
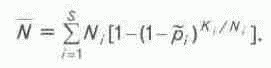
Для более полного удовлетворения спроса на нефть следует иметь в виду,
что спрос на определенное количество нефти требует подготовки соответствующего объема промышленных запасов. Их в свою очередь можно получить из определенного числа нефтяных структур, вмещающих перспективные ресурсы. В связи с этим особенно актуально определение числа и вероятности открытия месторождений из подготовленных структур.Если месторождения открываются с разной вероятностью
P1, P2,...PN, тогда вероятность открытия числа месторождений (r) из подготовленных N перспективных структур, на которых ведутся поисково-разведочные работы (PN,r), будет равняться коэффициенту переменной x' в разложении по степеням х следующей производящей функции ФN(х):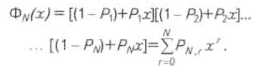
Если все нефтеносные объекты однотипны, т.е. имеют одинаковую вероятность открытия
P1=P2=...= PN=1-(1-P)K/N, тогда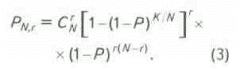
Имея в виду однотипность перспективных структур каждого класса, из
(3) получаем: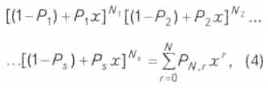
где
Pi(i= 1,2,...,S) – вероятность открытия одного месторождения i-го класса.Вероятность открытия месторождений из
Ni перспективных структур по каждому классу определяется по формуле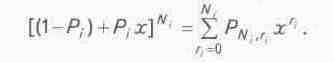
Пример
2. Требуется открыть четыре месторождения. Выделенные средства позволяют бурить четыре поисково-разведочные скважины. Вероятность открытия Pk одного месторождения с помощью K поисково-разведочных скважин равняется соответственно P1=0.3, P2=0,5, P3=0,6 и P4=0,8 (1, 2, 3, 4 - число скважин).Необходимо найти вероятность следующих событий:
а) не открыто ни одно месторождение;
б) открыто одно месторождение;
в) открыты два месторождения;
г) открыты три месторождения;
д) открыты все четыре месторождения.
Решение. При
N=4 и при вышеприведенных значениях Pi i= 1-4 производящая функция будет иметь следующий вид: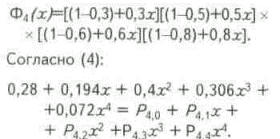
Таким образом, на четырех структурах, где ведутся поисково-разведочные работы:
а) вероятность открытия ни одного месторождения
P4.0 = 0,028;б) вероятность открытия одного месторождения
P4.1 = 0,194;в) вероятность открытия двух месторождений
P4.2 = 0,4;г) вероятность открытия трех месторождений
P4.3 = 0,306;д) вероятность открытия всех четырех месторождений
P4.4 = 0,072.Используя найденное значение
PN,r можно определить вероятность открытия не меньше чем заданного L числа (0<L<N) месторождений из подготовленных перспективных структур, на которых ведутся поисково-разведочные работы: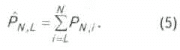
Пример
3. Поисково-разведочные работы ведутся (могут вестись) на четырех структурах. При условиях примера 2 найти следующие вероятности:а) открытие хотя бы одного месторождения;
б) открытие хотя бы двух месторождений;
в) открытие хотя бы трех месторождений.
Решение. Используем формулу
(5), тогдаа) вероятность открытия хотя бы одного (не менее одного) месторождения
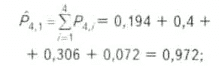
6) вероятность открытия хотя бы двух месторождений
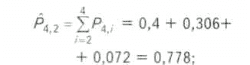
в) вероятность открытия хотя бы трех месторождений
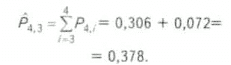
Капиталовложения в геофизические и поисково-разведочные работы на нефть связаны с риском получения безрезультатных исходов, поэтому требуется оптимизировать ведение работ и выбор возможной стратегии: например, увеличение доли детальных геолого-геофизических работ и сокращение затрат на поисково-разведочное бурение, интенсификация бурения в пределах подготовленных перспективных структур, перераспределение капиталовложений между геофизическими и поисково-разведочными работами и т.д.
Поскольку геофизические и поисково-разведочные процессы являются капиталоемкими, причем капиталовложения в них связаны с риском безрезультатности бурения, при их прогнозировании необходимо предусматривать достижение требуемого уровня эффективности при заданном уровне риска. В этом случае экономические критерии выбора решений должны быть адекватны характеру проводимых работ, в работе принимается минимум суммарных затрат на проведение геофизических и поисково-разведочных работ.
Примем следующие обозначения: С
– стоимость одной структуры, С' – стоимость одной поисково-разведочной скважины.Тогда стоимость геолого-геофизических работ будет составлять CN(u), стоимость поисково-разведочного бурения
– C'N'(u)n(u), а стоимость всех работz(u) = CN(u) + C'N'(u)n(u).
Требуется найти такое значение и, чтобы затраты z(u) были минимальными и вероятность попадания одной скважины в нефтеносный пласт р(и) была не меньше заданного числа
g О(0,1). Таким образом, приходим к следующей задаче математического программирования с вероятностными ограничениями: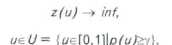
Для решения этой задачи разработан пакет компьютерных программ на основе алгоритма стохастического программирования (Юдин Д.В.,
1974).Определяя таким образом параметр и, можно вычислить: вероятность попадания одной скважины в нефтеносный пласт; вероятность открытия месторождений различного класса (по глубине залегания и их крупности); вероятность открытия заданного числа месторождений;
вероятность открытия не менее заданного числа месторождений; математическое ожидание числа открываемых месторождений и др.Разрабатываемая модель позволяет формировать и решать различные оптимизационные задачи определения оптимальных объемов геофизических, поисково-разведочных, а также эксплуатационных работ и их соотношения с использованием различных экономических критериев.
ЛИТЕРАТУРА
The article presents a mathematic model developed with regard to a stochastic character of the process allowing to determine the main indices of hydrocarbon resources development depending on the scope of information obtained during regional geologic-geophysical investigations. Among indices are the following: a probability of a single well entry into oil-bearing bed; a probability to discover fields of different classes (by occurrence depth and size of fields); a probability to discover the assigned number of fields; a probability to discover not less than the assigned number of fields; mathamatical expectation of a number of discovered fields.
The model under development allows to form and solve the various optimization tasks of determining optimal volumes of geophysical, exploration and production activities and their relation using different economic criteria.
РИС. 1. ЗАВИСИМОСТЬ
р(u) ОТ u ПРИ p0 = 0,1 И р* = 0,9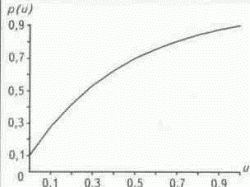
РИС. 2. ЗАКОН ОТКРЫТИЯ МЕСТОРОЖДЕНИЙ ПРИ РАЗЛИЧНЫХ ЗНАЧЕНИЯХ p