ПОВЕДЕНИЕ ГЛИНИСТЫХ ПОРОД ПРИ ЦИКЛИЧЕСКИХ НАГРУЗКАХ

Т.Н. Кольчицкая (ИПНГ РАН), Н.Н. Михайлов (РГУ нефти и газа им. И.М. Губкина)

При воздействии на пласт горная порода подвергается различным видам нестационарного нагружения. Однако особое внимание следует обратить на повторные переменные, или циклические, нагрузки. Такие циклические режимы имеют место при бурении, различных методах воздействия на пласт с целью повышения эффективности нефтеотдачи, эксплуатации подземных хранилищ газа (ПХГ), когда циклические процессы возникают не только в пласте-коллекторе, но и в глинистой покрышке. При закачке и отборе газа в ПХГ существенную роль играют деформационные процессы в околоскважинных зонах, которые также представляют собой заглинизированную породу. Периодические колебания напряженного состояния вызывают эффекты малоцикловой усталости, заключающиеся в изменении фильтрационных свойств пласта и структуры порового пространства. Экспериментально установлено, что прочность породы при динамической пульсирующей нагрузке снижается на 40-50 % (Мохначев М.П., 1979). Отношение усталостной прочности к статическому пределу прочности описывается убывающей логарифмической функцией от числа циклов. От последнего зависят также коэффициент Пуассона и модуль упругости, т.е. упругие характеристики породы.

Характерной особенностью глин являются малые размеры слагающих их частиц (< 2 мкм) и поровых каналов по сравнению с их поверхностью, что приводит к активному взаимодействию матрицы породы с насыщающим флюидом. Другая отличительная особенность глин - низкие фильтрационные свойства. Коэффициент проницаемости глин варьирует в пределах 10^-11-10^-13мкм². Деформация глинистой породы может вызвать не только изменение порового пространства, но и его фильтрационной способности. Существует мнение, что фильтрационные свойства глин обусловлены главным образом микротрещиноватостью породы. Трещинная проницаемость глин изменяется от 3*10^-13 до 5*10^-12 мкм² [2]. Именно наличие микротрещин, вызывающее дополнительную разность напряжений, определяет прочностные свойства глинистых пород. Поэтому достаточно некоторого импульса напряжений, чтобы произошел скачок деформации. Если напряжение в вершине микротрещины достигает критического значения, происходит дальнейший рост трещины или разрушение породы.

Отмечено, что при переменных нагрузках уже после небольшого числа циклов в породе появляются микротрещины, приводящие к ее разрушению. Это объясняется тем, что при циклическом нагружении вторичное поле напряжений меняется при переходе от одного цикла к другому и при определенной частоте циклов остаточные деформации отстают от изменения напряжения. Существующие и возникшие микродефекты и микротрещины не закрываются полностью и возвращения к начальному состоянию не происходит. Таким образом, под действием деформирующей нагрузки возможны либо дальнейший рост зоны с нарушенной структурой и увеличение проницаемости, либо уплотнение порового пространства и снижение фильтрационной способности. Изменение проницаемости может быть связано с переупаковкой частиц во внутрипоровом пространстве, вызванной разрушением скелета породы. Такие структурные изменения служит причиной гистерезиса проницаемости при циклическом воздействии на глинистый пласт.

Высокопористые глины являются молодыми отложениями с незавершенными процессами отжима из них поровой воды. Колебания напряженного состояния матрицы могут обусловливать изменение пористости, проницаемости и сжимаемости глин. Воздействие циклической нагрузки испытывает на себе не только скелет породы, но и насыщающий ее флюид. Под действием сжимающей нагрузки возрастает внутрипоровое давление. Если частота нагружения такова, что поровое давление не восстанавливается, то возникает его локальное повышение, которого может быть вполне достаточно для появления и развития трещиноватости.

Заглинизированность пласта, наличие как естественных, так и техногенных тупиковых пор снижают подвижность насыщающего флюида. Отсутствие возможности перетоков между порами способствует увеличению воздействия флюида на скелет породы, что не может не сказаться на изменении ее напряженно-деформированного состояния, от которого в свою очередь зависят и фильтрационно-емкостные характеристики.

В процессе формирования осадочных бассейнов существенную роль играют природные циклические процессы, являющиеся одной из причин образования глинистых пород с аномально высоким пластовым давлением. Под воздействием меняющегося пластового давления возникают деформация скелета породы и необратимые изменения ее физических свойств. Для случая геологических периодов циклических воздействий разработаны теоретическая основа прогнозирования аномально высоких пластовых давлений и методы определения напряженно-деформированного состояния глинистой породы [1]. Для случая техногенных циклических процессов, проходящих в других промежутках времени, данный подход некорректен и требует специального исследования.

Необходимость теоретического изучения поведения заглинизированного пласта под действием циклической нагрузки возникла в связи с проблемой повышения эффективности и надежности эксплуатации ПХГ. Основное внимание было уделено моделированию роста порового давления в глинистом пласте в результате циклического нагружения.

Построение математической модели связано с введением определенных ограничений. Будем считать процесс баротропным и рассмотрим состояние глины до ее разрушения. Тогда глинистый пласт можно рассматривать как упругое тело. Воспользуемся основными уравнениями механики сплошной среды [3]. В этом случае многомерная модель, описывающая состояние насыщенной пористой породы, находящейся под действием нагрузки, будет иметь вид

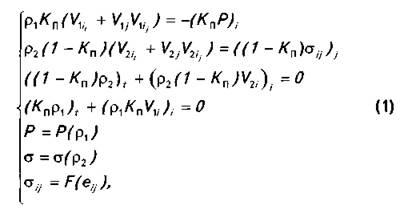
где V₁, V₂ - скорость движения флюида и матрицы соответственно;- плотность флюида и матрицы соответственно; Р- усредненное по объему давление пластовой воды; K_п - пористость;- усредненный по объему тензор напряжения и деформации матрицы породы соответственно;-шаровая часть тензора напряжений i, j - пространственные координаты; t - временная координата.

В дальнейшем систему (1) будем рассматривать относительно эффективных напряжений где- символ Кронекера. Считаем, что изменения пористости и плотности незначительны и перемещения малы, тогда можно будет пренебречь членами 2-го порядка малости.

Поровое пространство в глинах в основном занято гидродинамически неподвижной (связанной) водой, эффективная пористость (пористость, участвующая в фильтрации) примерно в 30 раз ниже общей пористости. Низкая фильтрационная способность глины, связанная и с ее структурными особенностями, позволяет не принимать во внимание возможность перетоков между отдельными порами. Таким образом, для глины можно считать, что скорости движения частиц жидкости и матрицы равны, т.е.

Вводя коэффициент сжимаемости флюида и скелета преобразуем систему (1) к виду

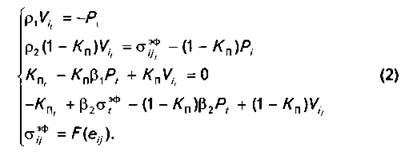
С введением обобщенного коэффициента сжимаемости и обобщенной плотности система (2) приводится к виду

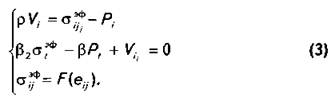
Для замкнутости систему (3) необходимо дополнить законом упругости, который в случае малых перемещений имеет вид

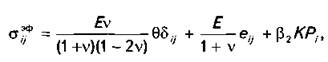
где- шаровая часть тензора деформаций матрицы; Е- модуль упругости; v - коэффициент Пуассона; - модуль объемного сжатия.

В этом случае система уравнений (3) может быть сведена к системе уравнений, зависящих только от напряжения в матрице и порового давления

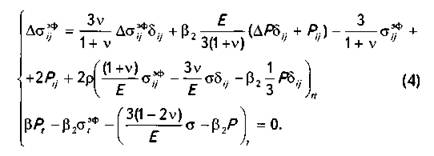
Рассмотрим решение данной задачи для условий полосы, т.е. предположим, что протяженность пласта велика по сравнению с его шириной (L » Н). К верхней границе полосы приложена равномерно распределенная постоянная нагрузка, тогда как нижняя граница подвергается циклическому воздействию. Считаем, что циклическая нагрузка приложена к матрице глинистого пласта. Выберем систему координат так, чтобы ось X совпадала с нижней границей пласта. Тогда граничные и начальные условия имеют вид

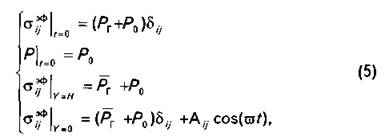
где - горное давление; Р₀ - начальное поровое давление; - приложенная циклическая нагрузка с частотой

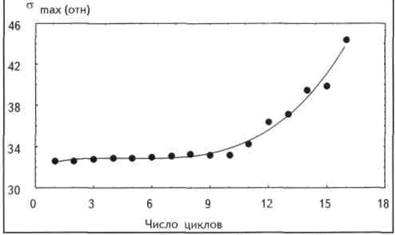
Система уравнений (4) существенно нелинейна, не допускает аналитического решения и требует применения численных методов. Для решения данной системы была выбрана локально-одномерная схема. Результаты счета представлены на рис. 1, рис. 2, рис. 3.

Результаты численного моделирования показали, что в случае циклической нагрузки при небольшом числе циклов характер изменения напряжения в матрице породы подобен таковому циклической нагрузки (см. рис. 1). Процесс чисто упругий. Однако при дальнейшем циклическом воздействии наблюдается увеличение амплитуд колебаний порового давления и эффективного напряжения (см. рис. 2), что может привести к возникновению пластических деформаций и структурным изменениям породы вплоть до ее разрушения.

Изменение скорости роста амплитуды колебаний эффективного напряжения с продолжительностью циклического нагружения демонстрирует рис. 3, на котором представлена зависимость амплитуды эффективного напряжения в матрице породы от числа циклов.

Модель позволила изучить изменение напряжения в матрице и порового давления в заглинизированных пластах. Результаты теоретических исследований хорошо согласуются с экспериментальными [4, 5]. Согласно экспериментальным и промысловым данным в процессе циклического воздействия амплитуда порового давления в течение некоторого промежутка времени остается постоянной. Одновременно с изменением давления поровой воды происходят незначительные деформации, которые можно отнести к упругим. По прошествии некоторого числа циклов наблюдается повышение скорости роста порового давления. Резкое возрастание амплитуды давления приводит уже к значительным деформациям. По всей видимости, происходящие структурные изменения в пласте позволяют стабилизировать давление поровой воды. Амплитуда давления в течение ряда циклов остается постоянной, однако пластические деформации продолжают нарастать, что приводит к разрушению структуры. В этом случае возможны разрушение глинистой покрышки и прорыв газа. В ряде случаев наблюдался отрыв пласта от глинистой покрышки, что приводило к образованию каверн.

В настоящей статье мы ограничились рассмотрением упругой циклической деформации глины. Однако, поскольку система уравнений (1), или преобразованная (3), относится к любому виду деформации, то предлагаемый подход может быть применим и в случае упруго-пластической и пластической деформаций, достаточно лишь заменить уравнение соответствующим закону деформирования.

В заключение отметим, что состояние насыщенного заглинизированного пласта, находящегося под действием циклической нагрузки, вполне удовлетворительно может быть описано системой нелинейных уравнений, основанных на концепции механики сплошной среды. Циклическое воздействие на пласт, изменяя напряженно-деформированное состояние среды, сказывается на структуре порового пространства и фильтрационно-емкостных параметрах. Результаты математического моделирования показали, что наличие в породе структурных "дефектов" накладывает определенные ограничения на режим циклического воздействия.

С помощью дренажа можно избежать разрушения при возникновении циклической подвижности. Дренаж вызывает рассеяние давления поровой воды, что позволяет не только стабилизировать, но и снижать избыточное давление. В связи с этим уже возникшие остаточные деформации не развиваются.

Возникновение пластических деформаций в процессе циклического нагружения пласта характерно не только для глинистых пластов. Высокая чувствительность напряженного состояния горных пород к различным вибрационным и сейсмическим воздействиям обнаружена при экспериментальных исследованиях, проводимых сотрудниками Института физики Земли (Николаев А.В., 1993). Отмечалось колебание пластового давления с изменением частоты, интенсивности и продолжительности воздействия. Исследования нефтяной залежи показали зависимость нефтеотдачи от параметров вибрационного воздействия. Подобные результаты позволяют считать эффекты циклической усталости пород значимыми для широкого круга проблем геологии и геофизики.

Литература

1. Добрынин В.М., Серебряков В.А. Методы прогнозирования аномально высоких пластовых давлений. - М.: Недра, 1978.

2. Кульчицкий Л.И., Ульяров О.Г. Физико-химические основы формирования свойств глинистых пород. - М.: Недра, 1981.

3. Седов Л.И. Механика сплошной среды. - М.: Наука, 1970.

4. Donald L.M., Raymond G.P. Repetitive load testing: reversal or rotation // Can. Geotech. J. - 1984. - Vol. 21, № 3. -P. 456-474.

5. Paoliani P. A method for evaluating pore pressure rise during dynamic loading of sands // Soil Dynamics and Earthquake Engineering. - Berlin, 1985. - P. 3-65 - 3-74.

In this study the state of saturated slayey layer under cyclical load is descrived with a system of non-linear equations based on usual approaches of continuum mechanics. This mathematical model permits to study changes of the pore pressure and of the rock matrix stress. The results of the mathematical modeling indicate that the presence of the structure "defects" in the imposes restrictions onto the regimes of cyclical loading which do not cause irreversible deformation.

Рис. 1. ИЗМЕНЕНИЕ НАПРЯЖЕНИЯ В МАТРИЦЕ ПОРОДЫ ПРИ ВОЗДЕЙСТВИИ ЦИКЛИЧЕСКОЙ НАГРУЗКИ ДО НАЧАЛА ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ

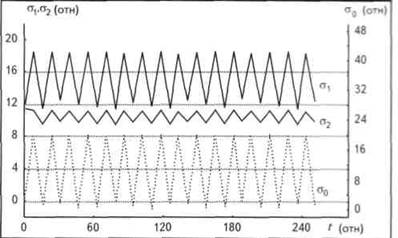
- циклическое воздействие на границе у = 0;- эффективные напряжения вблизи границы у = 0 и у = Н/3 соответственно

Рис. 2. ИЗМЕНЕНИЕ НАПРЯЖЕНИЯ В МАТРИЦЕ ПОРОДЫ (А) И ВНУТРИПОРОВОГО ДАВЛЕНИЯ (Б) ПРИ ЦИКЛИЧЕСКОМ ВОЗДЕЙСТВИИ В ПЕРИОД НАЧАЛЬНЫХ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ

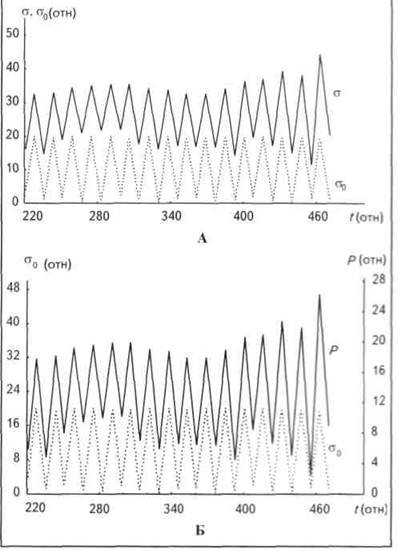
Рис. 3. ИЗМЕНЕНИЕ АМПЛИТУДЫ НАПРЯЖЕНИЯ В МАТРИЦЕ ЗАГЛИНИЗИРОВАННОЙ НАСЫЩЕННОЙ ПОРОДЫ ПРИ ЦИКЛИЧЕСКОМ ВОЗДЕЙСТВИИ