|
© В.П. Ластовецкий, 2001 |
НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ, ЕГО СВЯЗЬ С ФИЛЬТРАЦИОННО-ЕМКОСТНЫМИ СВОЙСТВАМИ ПОРОД И ГРАВИТАЦИОННЫМ ПОЛЕМ
(на примере Юрубченского нефтегазоконденсатного месторождения)
В.П. Ластовецкий (ОАО "ЗапСибгеология")
На глубине горные породы находятся под воздействием многих физико-механических факторов: массы вышележащих пород, тектонических сил различного направления, внутреннего давления насыщающих флюидов и др. Все это приводит к возникновению в массиве горных пород сложного объемно-напряженного состояния. Поскольку массив состоит из неоднородных по физико-механическим свойствам горных пород, обладает определенной геометрией, характеризуется расчлененным в разной степени рельефом на поверхности, то в поле напряжений возникают аномальные зоны относительного растяжения, сжатия и сдвига. Очевидно, что в этих условиях подвижные жидкие или газообразные флюиды будут мигрировать из зоны относительного сжатия в зону относительного растяжения. Считается, что заполнение многих нефтегазовых структур произошло в палеогене - неогене, когда в основном сложилась наблюдаемая ныне геологическая картина, возник современный рельеф дневной поверхности, т.е. формирование нефтегазовых залежей происходило при сильном влиянии современного напряженно-деформированного состояния (НДС) массива горных пород. Для залежей более древнего происхождения их устойчивое сохранение также невозможно без наличия определенных соотношений в полях напряжений.
Математическое моделирование НДС массива горных пород применительно к нефтегазопоисковым задачам показано в работе В.О. Каледина и В.П. Ластовецкого (1999). Здесь путем расчета объемных полей напряжений методом конечных элементов (МКЭ) в линейно-упругой постановке с применением специальной обработки выделяются зоны относительного растяжения и сдвига (повышенной трещиноватости, с улучшенными фильтрационно-емкостными свойствами (ФЕС), которые благоприятны для скопления УВ. Вопросы техники вычислений, оценки точности апробированы на Межвузовской научной конференции "Численно-аналитические методы решения краевых задач" 12-13 ноября 1999 г. в Новокузнецке (Ластовецкий В.П., 1999).
При детальной разведке УВ появляется возможность корреляционной увязки напряжений с ФЕС нефтяного пласта. Так как нефтяной пласт оказывается в неоднородном поле напряжений, то оно отражается на ФЕС пласта. Выявив такие связи, можно прогнозировать ФЕС на еще не изученной или слабо изученной территории.
Прежде чем перейти к рассмотрению результатов, полученных на Юрубченском нефтегазоконденсатном месторождении, заметим, что в условиях, когда константы, определяющие деформации и прочность горных пород, неизвестны либо заданы приближенно, упругие модели позволяют получить, по крайней мере, качественную картину распределения напряжений и в то же время служат основой для построения нелинейных и неупругих моделей. В литературе описаны случаи применения таких сложных моделей: билинейной среды (с разной диаграммой напряжения на сжатие и растяжение); контакт-элемента, имитирующего тектонический разрыв, который сопротивляется не растяжению, а только сжатию и сдвигу за счет смыкания стенок трещины, и других упругопластичных и вязкоупругих моделей [5]. Имеются примеры описания расчетов НДС сложного реального массива, состоящего из рыхлых и скальных пород с разрывными нарушениями, для которых задаются свои законы деформации. При этом все расчеты ведутся лишь для двухмерной среды. Замечательный результат получен по расчету сдвижения горных пород при разработке нефтяных месторождений [4]. Сдвижение горных пород, вызванное добычей нефти и газа, связано с уплотнением под действием нагрузки толщ пород, перекрывающих истощенные резервуары-коллекторы. Мульда сдвижения может иметь оседания от нуля до нескольких метров в зависимости от физико-механических свойств вмещающих пород и коллектора. В качестве модели принята "шатровая" упрочняющаяся модель деформирования коллектора под нагрузкой в двухмерной постановке, в которой учитываются как нелинейноупругие, так и вязкопластичные (необратимые) деформации. Расчет выполнен для Верхнекамского нефтяного месторождения, которое территориально совмещено с Верхнекамским месторождением калийно-магниевых солей, разрабатываемым подземным способом, чем и объясняется важность выполненных прогнозов. Авторы [4] имели в своем распоряжении материалы геодезических съемок поверхности проседания и на каждом шаге инкрементальной процедуры корректировали расчеты, сверяясь с данными нивелирования.
Таким образом, для проведения расчетов в нелинейной и неупругой постановке необходимы данные о полной диаграмме "напряжение - деформация", включающей и запредельную область, а также константы, определяющие неупругие свойства пород. Для нашего направления исследований - объемное моделирование НДС применительно к нефтепоисковым задачам - получение таких данных весьма проблематично. Так, существует методика оценки горного давления по данным акустического каротажа с учетом тарировочных зависимостей. Под горным давлением понимается вертикальная компонента нормального вектора напряжений - sz. Даже если эта методика эффективна, то все равно для оценки полного вектора этого недостаточно. Других объективных подходов здесь пока не имеется, хотя расчеты гипотетических моделей возможны.
Поля напряжений
Юрубченское месторождение входит в состав гигантской Юрубчено-Тохомской зоны нефтегазонакопления Сибирской платформы [2]. На площади Юрубченского месторождения, покрытого густой сетью сейсмических профилей ОГТ, пробурено около 70 разведочных скважин с полным комплексом испытаний и каротажных исследований.
Кратко геологическое строение месторождения сводится к следующему: сложнопостроенный фундамент архей-протерозойского возраста перекрывается осадочным чехлом, сложенным породами рифея, венда и кембрия. Основные скопления нефти и газа приурочены к доломитовым толщам рифея. Кровля рифейских отложений представляет собой размытую поверхность, которую несогласно перекрывают глинисто-солевые отложения нижнего палеозоя, прорванные дайками и силлами долеритов мезозоя. В тектоническом плане породы нижнепалеозойских свит - почти горизонтально-слоистые образования, а рифейских - сложнодислоцированные структуры.
Расчеты НДС Юрубченского месторождения выполнены по программе, реализующей обычную процедуру МКЭ [3] в линейно-упругой трехмерной постановке. Объемная конечно-элементная модель месторождения представляет собой параллелепипед со сторонами 82.0x32.0x3.5 км, или 42x33x25 узлов, находящийся под действием сил собственной массы, т.е. модель состоит из 31488 конечных элементов с 34650 узлами, что приводит к системе линейных алгебраических уравнений с ~105 неизвестными перемещениями. На верхней поверхности модели задан реальный рельеф местности с отметками высот 190-700 м. Граничными условиями служило закрепление узлов (нулевые перемещения) на боковых гранях и дне модели по направлениям, перпендикулярным к этим плоскостям. Ускорение свободного падения принято равным 9,8 м/с2.
При задании физико-механических свойств пород для каждого элемента введены плотность (r), модуль Юнга (Е) и коэффициент Пуассона (m), конечные элементы образуют в модели слои-свиты. Упругие характеристики получены путем пересчета скоростей продольных (Vp) и поперечных (Vs) волн по известным формулам. Скорости определены по данным акустического каротажа, измерений на керне с учетом материалов наземной сейсморазведки. Геомеханические характеристики свит даны в табл. 1 .
Наиболее плотными породами в разрезе являются долериты траппов (3,04 г/см3) и доломиты (2,77-2,82 г/см3) булайской, тэтэрской, собинской, катангской, каланской и юрубченской свит. Для этих свит характерны также повышенные значения Е и пониженные m. Между ними залегают ангидрит-глинисто-солевые отложения пониженных плотности и упругих модулей. В целом разрез можно охарактеризовать как слабоконтрастный.
Результатами расчетов являются поля нормальных sх,y,z и касательных txy,xz,yz напряжений и нормальных ex,y,z и касательных gxy, xz, yz деформаций. Обе группы параметров примерно одинаково отображают полученные результаты, тем не менее, предпочтение отдано напряжениям как наиболее информативным. При этом касательные напряжения крайне малы и составляют около 0,01 от нормальных, т.е. сдвиговые деформации в исследуемой модели практически не создаются. Исключение составляют приповерхностные области, где сильно влияние пересеченного рельефа местности. Здесь касательные напряжения соизмеримы с нормальными, а нормальные напряжения могут быть разного знака вплоть до абсолютного растяжения.
На рис. 1 показано поле напряжений sx по одному из вертикальных сечений модели Абсолютное поле напряжений (см. рис. 1 , A) с целью уточнения результатов численных расчетов приведено к упругой модели Динника, как наиболее полно отвечающей упругопрочностным свойствам большинства горных пород. Как видно на рис. 1 , А, абсолютное поле напряжений sх в вертикальном сечении представляет собой картину линейного нарастания напряжений с глубиной, заметно осложненную аномалиями за счет неоднородного строения модели и рельефа поверхности. Чтобы сделать эти аномалии более наглядными, из абсолютных значений напряжений был вычтен линейный фон, определенный методом наименьших квадратов. Эта операция имеет глубокий физический смысл из поля напряжений неоднородного массива удаляется влияние геометрически того же, но однородного по геомеханическим свойствам массива. Здесь просматривается аналогия с обработкой гравитационного поля: из поля абсолютного притяжения удаляют влияние известных масс и получают знакопеременные локальные поля относительно большего или меньшего притяжения. Так и при обработке полей напряжений из поля общего сжатия выделяют участки относительно меньшего сжатия (зоны относительного растяжения) и участки относительно большего сжатия (зоны относительного сжатия). Как видно на рис. 1 , Б, на котором для наглядности совмещены поля относительных напряжений с контурами модели (см. рис 1 , В), более плотным и прочным породам (к ним же относятся рифейские доломиты коллектора) соответствуют в основном зоны относительного растяжения, а слабым породам - зоны относительного сжатия.
На рис. 2 показано поле относительного напряжения sx на эрозионной поверхности рифея. Эрозионная поверхность рифея по данным бурения и сейсморазведки представляет собой очень пологое поднятие с углами падения менее 1°. На эту поверхность в северо-западной и северо-восточной частях, кроме доломитов, выходят глины рифея и гранитогнейсы архей-протерозоя, уже не являющиеся коллекторами УВ. Как видно из рис. 2 , сложное геологическое строение массива в совокупности с рельефом местности создает на глубине 2200-2600 м довольно причудливую картину распределения относительных растяжений и сжатий.
Сопоставление значений sx, y, z, рассчитанных для поверхности рифея, со значениями ФЕС по данным исследования керна и испытания пластов, приводит к соответствующим диаграммам рассеяния ( рис. 3 ).
Наиболее тесная зависимость отмечается между относительными напряжениями и коэффициентом пористости (вторичной пустотности) (Кп) коллектора, который использовался при подсчете запасов месторождения. В табл. 2 даны парные коэффициенты корреляции этих величин.
Линейное многомерное уравнение связи между этими параметрами имеет вид
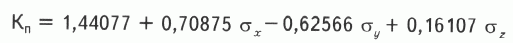
Статистическая оценка меры сходства R-квадрат = 36,5 %, т.е. 36,5 % дисперсии коэффициента пористости обусловлено параметрами НДС. Среднеквадратическая ошибка прогноза пористости равна ±0,54 %. Диаграмма рассеяния прогнозной и измеренной пористости показана на рис 3 , А. Сопоставление в плане прогнозной согласно уравнению и измеренной на керне пористости дано на рис 4 , где видна вполне приемлемая степень их совпадения, что делает эту информацию пригодной для проектирования мест заложения новых скважин.
Корреляционные связи относительных напряжений с дебитами (см. рис. 3 ,Б) и проницаемостью (см. рис. 3 ,В) менее тесны и характеризуются большим разбросом значений. Тем не менее, хорошо видна качественная зависимость: чем больше относительное растяжение, тем выше значения дебитов и проницаемости.
Большой разброс значений дебитов (1-660 м3/сут) и проницаемости (0,0001-2,2500 мкм2) можно объяснить следующим согласно К.И. Багринцевой [1], рифейский коллектор является трещинным и каверново-трещинным. Густота первичных трещин связана с литологической неоднородностью доломитов. Вторичные каверны развиты в основном по вертикальным трещинам. Их размеры, зафиксированные в керне, достигают 0,5x10,0 см. В природных условиях возможны пустоты выщелачивания вплоть до расщелин и карстовых полостей, что подтверждают случаи провала бурового инструмента, интенсивного поглощения промывочной жидкости и снимки телеметрии скважин. Особенностью вертикальных трещин, расширенных выщелачиванием и заключающих, видимо, основной объем УВ, является их редкий шаг - расстояние между ними составляет 3-5 см и более. Отсюда следует, что вертикальная скважина, имеющая диаметр 190 мм, пересекает в коллекторе 4-6 и менее таких трещин. Таким образом, дебит скважины во многом зависит от "удачного" в вышеуказанном смысле ее расположения. Выходом из такой ситуации могло бы быть бурение скважин с горизонтальным завершением либо проходка боковых стволов из старых скважин. При этом при задании их пространственного азимута следует учитывать данные расчета НДС. Так как коллектор характеризуется сложнонапряженным состоянием: сжатием по вертикали и относительным растяжением по горизонтали, то максимальное раскрытие за счет НДС будут иметь те вертикальные трещины, которые ориентированы перпендикулярно к полному горизонтальному вектору относительного растяжения. Задав азимут искривления скважины вдоль вектора, можно обеспечить максимальные притоки за счет пересечения наибольшего числа максимально раскрытых вертикальных трещин. Картина расположения полных горизонтальных векторов напряжений sх + sу показана на рис. 5 . Здесь видно, что в контуре залежи векторы относительного растяжения имеют ориентировку с юго-запада на северо-восток при азимуте около 45°. В этом направлении и следует ориентировать горизонтальные стволы.
Гравитационные поля
Из вышеописанного видно, что при подготовке геомеханической модели месторождения для расчета НДС составной частью в нее входит и плотностная модель, т.е. появляется возможность без дополнительных затрат на подготовку данных выполнить расчет для гравитационного поля модели. Такая программа составлена А.Н. Цветковым (КемГУ). Программа использует данные файлов координат узлов и топологии модели и выполняет расчет гравитационного поля в узлах, расположенных на поверхности модели. В основу расчета положено поле произвольного шестигранника.
Программа оттестирована на примерах с известным решением. При подготовке модели для расчета НДС, для того чтобы добиться необходимой точности расчетов, модель приходится разбивать на большое число конечных элементов - шестигранников, поэтому при расчете гравитационного поля экономия на вводе данных компенсируется большим временем собственно счета. В дальнейшем, сопоставляя расчетное поле модели с наблюденным, выполняют обычную процедуру интерпретации, принятую в гравиразведке.
На рис. 6 , А показана карта аномалии Dg Буге для плотности 2,5 г/см3 в условном уровне, полученная по результатам гравиметрической съемки масштаба 1:200 000. Плотность пород промежуточного слоя 2,5 г/см3 соответствует плотности пород пролетарской О1pr и эвенкийской €2-3 ev свит, залегающих в интервале от поверхности до отметки уровня моря 0 м.
На рис. 6 , Б дано поле локальных аномалий, полученное путем удаления из наблюденного поля кубического тренда, что соответствует удалению влияния глубинной части разреза - свыше 3-5 км.
На рис. 6 , В показано гравитационное поле, рассчитанное от заданной модели, при этом плотность 2,5 г/см3 принята за нулевую.
Учитывай геологическое строение разреза, можно утверждать, что нижнепалеозойская осадочная толща, представляющая собой практически горизонтальные слои, не будет создавать локальных аномалий Dg. Здесь могут сказываться лишь небольшое влияние рельефа местности, выходы на поверхность даек и выклинивание силлов долеритов. Некоторое воздействие на поле Dg может оказывать неровная эрозионная поверхность рифея. В пределах изучаемой территории ее отметки колеблются от -1950 м в центре до -2250 м на юго-западном фланге, что дает углы падения менее 1°. Основное же влияние на локальное поле Dg будет оказывать неоднородное строение фундамента, который разбит дизъюнктивами на блоки различных размеров с внутренней более интенсивной складчатостью. Таким образом, участки с повышенными значениями Dg отвечают площадям выходов на эрозионную поверхность доломитов как наиболее плотных пород, а участки с пониженными значениями Dg - выходам аргиллитов вэдрэшевской свиты R1-2vdr или гранитогнейсов архей-протерозоя.
Сопоставляя гравитационные поля на рис. 6 , Б и 6,В, замечаем, что в локальных полях рис. 6 , Б четко проявились две вытянутые с юго-запада на северо-восток зоны пониженных значений Dg с амплитудой до 0,006 см/с2, приуроченные к полям доломитов юрубченской свиты. При этом центральная зона имеет сложную конфигурацию, а восточная, видимо, представляет собой фрагмент более крупной зоны. Учитывая вышеприведенные соображения об источниках аномалий, можно сделать вывод о том, что выявленные зоны не что иное, как зоны сверхвысокой трещиноватости и разуплотнения доломитов и развития палеокарста. Несложный расчет по формуле плоскопараллельного слоя показывает, что при увеличении пористости (пустотности) доломитов до 20 % слой мощностью 100 м создает отрицательную аномалию 0,0024 см/с2, что соизмеримо с наблюденными локальными полями. К сожалению, автор не располагает полными данными по каждой скважине в отдельности, чтобы проанализировать их с этой точки зрения и доказать или опровергнуть высказанное предположение.
Необходимо отметить, что при создании геомеханической модели Юрубченского месторождения для расчета НДС области разуплотнения доломитов не моделировались и все доломиты принимались одной плотности. Однако при появлении таких данных их легко можно учесть и пересчитать поля. Поскольку НДС в доломитах юрубченской свиты определяется в основном распределенной массой вышележащих пород, которые не меняют своих свойств, и характеристиками самих доломитов, то можно предположить, что в результате введения участков трещиноватых и закарстованных "слабых" доломитов последние станут концентраторами напряжений. Тогда область относительного растяжения (см. рис. 2 ) может распасться на отдельные изолированные участки.
Очевидно, что надежность и достоверность прогнозирования НДС массива горных пород, как и при решении других прямых задач геофизики, в первую очередь зависят от полноты и достоверности исходной геологической информации, касающейся его строения и геомеханических свойств горных пород.
Заключение
На примере Юрубченского нефтегазоконденсатного месторождения показано:
Литература
The mathematical modelling by a method of finite elements in linear-elastic statement of strain-deformed state of Yurubchen oil and gas field is described. The zones of a relative extension and compression are allocated. The correlation connection between relative stresses and reservoir porosity is established, the strain association with other filtration and capacious properties is shown. The gravitational fields are compared, measured and calculated, the disconsolidation zones are allocated. It's drawn a conclusion about application of the given technique at different stages of prospecting works.
|
Свиты, породы |
r . г/см3 |
Vp, m/c |
Vs, m/c |
m |
Е, МПа |
|
|
Долериты траппов |
b T1 |
3,04 |
6580 |
3700 |
0,269 |
105626 |
|
Пролетарская + эвенкийская |
|
2.50 |
5490 |
3000 |
0,287 |
57915 |
|
Литвинцевская + ангарская |
|
2.58 |
5690 |
3090 |
0,291 |
63605 |
|
Булайская |
|
2,77 |
6510 |
3600 |
0,280 |
91901 |
|
Вельская |
|
2,59 |
5730 |
3050 |
0,302 |
62738 |
|
Усольская |
|
2,53 |
6250 |
3100 |
0.337 |
65013 |
|
Тэтэрская + собинская |
|
2,80 |
6450 |
3280 |
0,326 |
79886 |
|
Катангская |
Vktg |
2,75 |
6600 |
3500 |
0,304 |
87855 |
|
Оскобинская |
Vosk |
2,63 |
6800 |
3600 |
0,305 |
88991 |
|
Каламская |
R1-2kl |
2,80 |
6930 |
3730 |
0,296 |
100984 |
|
Юрубченская |
R1-2jur |
2,82 |
7000 |
3770 |
0,296 |
103887 |
|
Вэдрэшевская |
R1-2vdr |
2,68 |
5300 |
2860 |
0,297 |
56730 |
|
Гранитогнейсы фундамента |
AR-PR |
2,67 |
6500 |
3660 |
0,268 |
90702 |
|
Параметры корреляции |
Кп |
s x |
s y |
s z |
|
Кп |
- |
0,5638 |
0,5118 |
0,5568 |
|
s x |
0,5638 |
- |
0,9660 |
0 8990 |
|
s y |
0,5118 |
0 9660 |
- |
0,9117 |
|
s z |
0 5568 |
0,8990 |
0,8990 |
- |
Рис. 1. ПОЛЯ НАПРЯЖЕНИЙ
sx В СЕЧЕНИИ А-А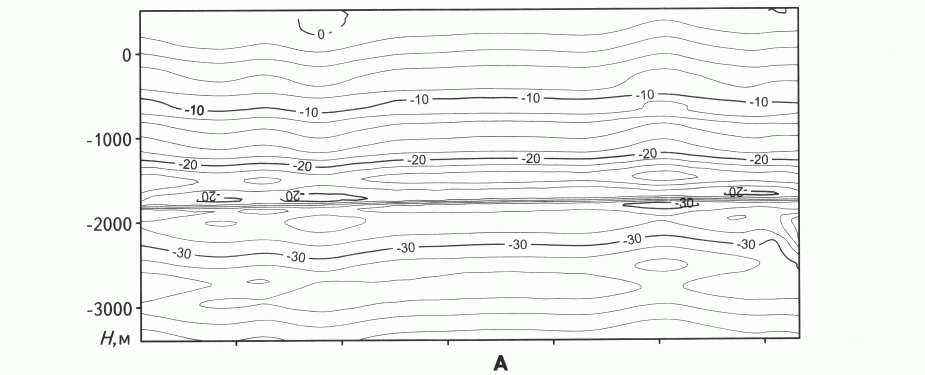

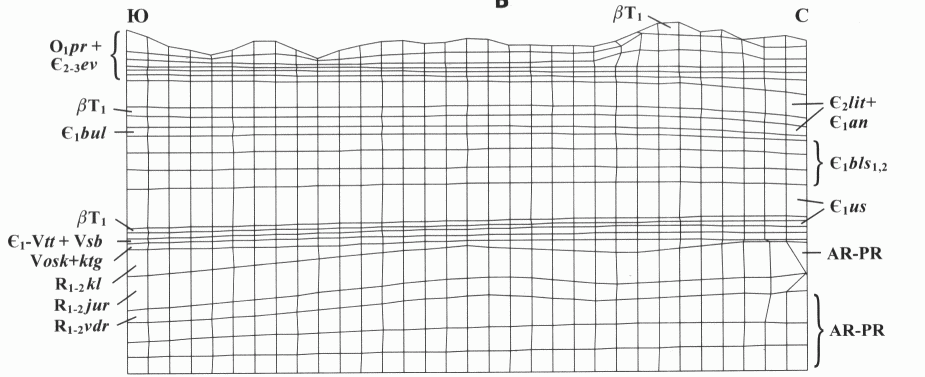
А - абсолютные напряжения Мпа; Б - относительные напряжения; МПа В - конечно-элементная модель; 1 изолинии напряжения: а положительные, б – отрицательные, в – нулевые. Положение сечения см. на рис. 2.
Рис. 2 КАРТА ПОЛЕЙ ОТНОСИТЕЛЬНЫХ НАПРЯЖЕНИЙ НА ПОВЕРХНОСТИ РИФЕЯ И ПОРИСТОСТИ (ВТОРИЧНОЙ ПУСТОТНОСТИ) КОЛЛЕКТОРА
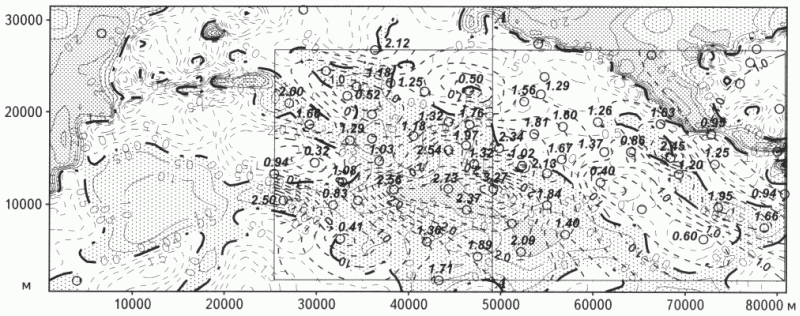

Зоны относительного 1 - растяжения 2 – сжатия; 3 - изолинии пористости %; 4 - скважины разведочного бурения и значения пористости коллектора в них %; 5 - положение сечения. Остальные усл. обозначения см. на рис. 1.
Рис. 3. ДИАГРАММЫ РАССЕЯНИЯ
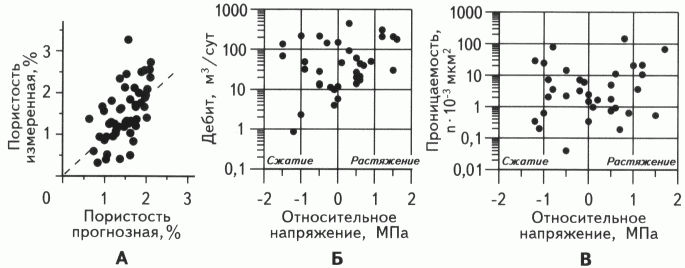
А - измеренной и прогнозной пористости; Б - дебитов и относительных напряжений; В - проницаемости и относительных напряжений.
Рис. 4. КАРТА ИЗМЕРЕННОЙ И ПРОГНОЗНОЙ ПОРИСТОСТИ
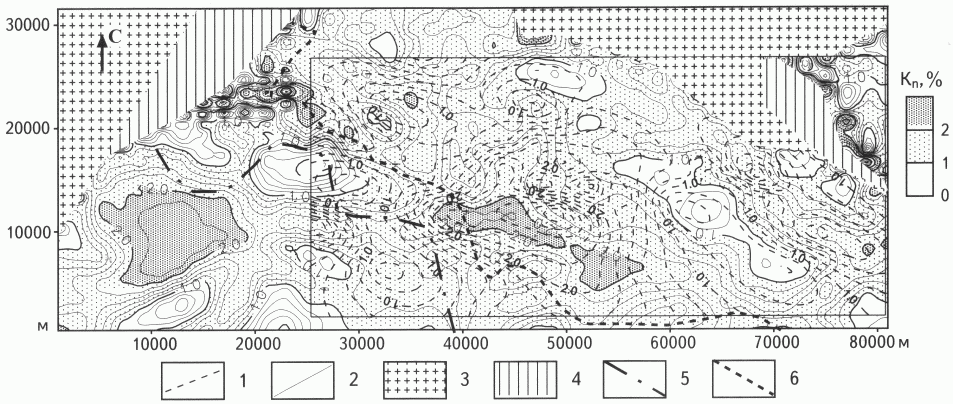
Изолинии пористости %: 1 - измеренной, 2 – прогнозной; выходы на эрозионную поверхность рифея: 3 - архей-протерозойского фундамента, 4 - глин рифея; 5 – ВНК, 6 - ГНК
Рис. 5. КАРТА ПОЛНЫХ ГОРИЗОНТАЛЬНЫХ ВЕКТОРОВ ОТНОСИТЕЛЬНЫХ НАПРЯЖЕНИЙ
sx + sy.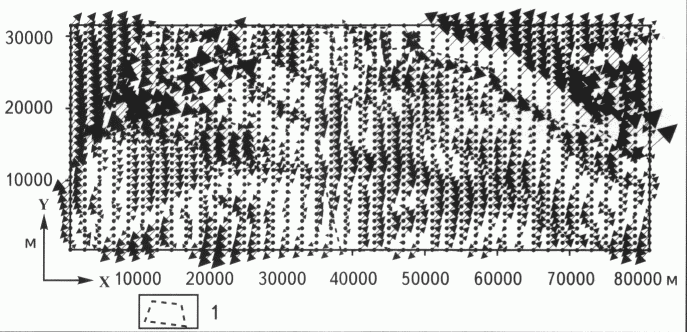
1 - контур залежи
Рис. 6. КАРТЫ ГРАВИТАЦИОННЫХ ПОЛЕЙ
|
|
|
|
|
|
|
|
A - наблюденного поля
DgБ (2.5 г/см3); Б - остаточных аномалии; В - вычисленного поля; 1 - зоны разуплотнения