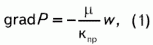
|
© Коллектив авторов, 2001 |
ОБОСНОВАНИЕ ИСПОЛЬЗОВАНИЯ СЕЙСМОАКУСТИЧЕСКИХ МЕТОДОВ ДЛЯ ОЦЕНКИ ПРОНИЦАЕМОСТИ ГОРНЫХ ПОРОД
О.Л. Кузнецов (ВНИИгеосистем), В.Ш. Халилов, Р.Р. Гафуров (БГУ), К.В. Антонов (Управление по недрам (Башкортостан), А.Г. Болгаров (ОАО НПП ВНИИГИС)
Работы по исследованию фильтрационных характеристик пластов с помощью поверхностных волн проводятся с начала 80-х гг. Методика оценки проницаемости горных пород, основанная на измерении амплитуды трубной волны, генерируемой проницаемым пластом горных пород на пересечении со скважиной [1], предусматривает измерение полного вектора смещения пород на стенке скважины и вычисление отношения амплитуды давления в трубной волне к амплитуде полного вектора скорости смещения пород на стенке скважины. По этому отношению судят о проницаемости пород. Но необходимо отметить, что получаемая информация недостаточно полноценна, поскольку исследованию подвергается лишь ограниченная прискважинная зона. Поверхностный характер волны Лэмба-Стоунли не позволяет судить о процессах, происходящих в глубине нефтеносных пластов, и об их внутренних свойствах. С повышением точности измерительных приборов стало возможным появление более совершенных методик оценки внутренних характеристик пластов
Теоретические работы, проводимые в БГУ с 1984 г. (Халиков Г.А., Халилов В.Ш., 1985, Халилов В.Ш., Бандов В.П., Муртазин Х.Х., Замалетдинов М.А , 1988; Халилов В.Ш., Бандов В.П., Гильманов А.А., Малинин В.Ф., 1992), показали возможность оценки фильтрационных характеристик горных пород с помощью продольных волн. В основу такой оценки должен быть положен следующий физический механизм. При распространении упругой волны на ее фронте происходят фильтрационные перетоки порового флюида, приводящие к изменению упругих свойств среды. Известно, что модули упругости сухой и насыщенной пористых сред могут отличаться более чем на четверть (Бандов В.П., Халилов В.Ш., 1992). Ввиду квадратичной зависимости эффективного объемного модуля среды от скорости продольной волны последняя при изменении насыщенности среды может изменяться более чем на 10 %. Следствием существования эффекта фильтрационных перетоков на фронте упругой волны является возможность получить изменение ее кинематических и динамических параметров, зависящих от проницаемости среды и свойств жидкости, через изменение входных параметров волны (амплитуды и частоты). Для количественной оценки указанных зависимостей необходим более детальный микроструктурный анализ взаимодействия составляющих фаз на фронте волны. Использование идеализированных моделей деформации скелета пористой среды и фильтрационных течений в порах дает возможность учесть взаимодействие указанных процессов.
Пусть поровая жидкость фильтруется по одномерному поровому каналу или, другими словами, по каналу, течение в котором носит одномерный характер, со скоростью (w), связанной с давлением (P) соотношением Дарси.
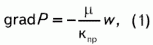
где m - вязкость флюида, кпр - проницаемость
В левой части уравнения (1) стоит вынуждающая сила, приходящаяся на единицу объема порового канала. Если в качестве этой силы выступает сила давления плоской акустической или сейсмической волны вида
 амплитуда смещения. Здесь учтено, что отношение с =w/k - фазовая скорость распространения волны, где k - амплитуда волнового вектора k. Амплитуда смещения поровой жидкости на практике может изменяться в пределах 10-15-10-5 м.
амплитуда смещения. Здесь учтено, что отношение с =w/k - фазовая скорость распространения волны, где k - амплитуда волнового вектора k. Амплитуда смещения поровой жидкости на практике может изменяться в пределах 10-15-10-5 м.
Полученный результат можно интерпретировать следующим образом. При распространении сейсмоакустических волн по насыщенной флюидом пористой среде в каждом из цилиндрических капилляров, составляющих идеализированное пространство порового пласта, происходит смещение жидкости в направлении распространения волны, амплитуда которого прямо пропорциональна амплитуде волны и проницаемости пористой среды и обратно пропорциональна вязкости флюида, насыщающего поры, и скорости распространения волны.
Если, как в [2, 5], добавить к левой части соотношения (1) силы инерции, то уравнение движения в комплексной записи для единичной массы жидкости приобретет вид
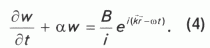
Здесь в правой части мы имеем градиент давления, взятый со знаком "минус" и деленный на плотность флюида, а в левой - сумму сил инерции и сопротивления. Постоянные a и В определяются через параметры пористой среды и акустической волны следующим образом:
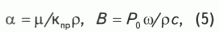
где r - плотность флюида.
Решение неоднородного дифференциального уравнения (4) несложно, в итоге для смещения флюида при t ->Ґ получаем:
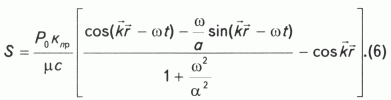
Так как a =m/кпрr = 107-1011 с-1, то (6) сводится к (2). В применении к уравнению движения флюида (4) это означает, что силы инерции для нашей задачи пренебрежимо малы практически для любой частоты воздействия. Это значит, что выражение для смещения жидкости (2) с амплитудой (3) является справедливым практически для любой частоты динамического воздействия.
Рассмотренная картина течения флюида является одномерной. В случае продольной волны колебания некоторого объема пор приведут к их периферическому сжатию и расширению. Для оценки гидродинамических эффектов в пористой среде возьмем идеализированную структуру, состоящую из параллельных мембран, совершающих колебательные движения. При этом мембраны бесконечны вдоль осей OX, 0Z и удалены друг от друга на расстояние d = 2R. Пусть между пластинами покоится вязкая несжимаемая жидкость, а пластины - границы жидкости - совершают колебательные движения по закону у0 (x,t) ( рис. 1 ). Расстояние между пластинами, или поперечный размер поры, пренебрежимо мало по сравнению с длиной волны l, т.е. d << l, что справедливо для подавляющего большинства практически важных случаев. Требуется найти поле давлений волны, скоростей и смещений жидкости. Параметрами являются следующие основные характеристики процесса: частота, скорость и амплитуда волны, а также проницаемость среды.
Смещение жидкости в области х >=0, -R =<у =< R математически представимо в виде системы уравнений гидродинамики:
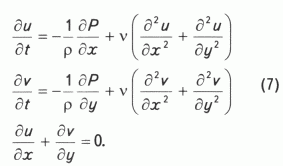
Она состоит из уравнений Навье-Стокса для двух компонент скорости - продольной u и поперечной v, в которых ввиду малых значений скоростей отброшены конвективные члены, квадратичные по скорости, а также уравнения неразрывности. Здесь Р- давление в поровом канале, v =m/r - кинематическая вязкость жидкости.
Продифференцировав первое уравнение (7) по координате х, а второе - по координате у, сложив их и подставив в третье уравнение системы (7) - уравнение неразрывности, получим следующую систему уравнений:
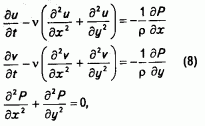
для которой необходимо теперь сформулировать граничные условия.
Граничные условия для первого уравнения (8) ввиду А << R, что говорит о практически фиксированном положении границ y1 = -R, у2 = R, имеют вид u(х, -R,t)= u(x,R,t) = 0, где А - амплитуда смещения границы порового канала, R - размер порового канала.
Вследствие гармонического движения границ области граничные условия для поперечной компоненты скорости выглядят следующим образом:
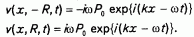
Сформулируем граничные условия для давления в уравнении неразрывности. Для этого примем в качестве уравнения состояния порового флюида упрощенное уравнение Тейта q2 = Р/gА, справедливое для малых амплитуд давления, когда выполняется условие малости линейной деформации объема жидкости А в сравнении с размером порового канала R: А << R. Здесь g - упругая постоянная жидкости, q2 - относительное изменение объема жидкой фазы. В то же время из рис. 1 видно, что для фиксированного сечения канала можно записать
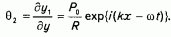
Из последнего выражения для q2 получим функцию давления на границе канала
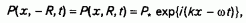
где Р* =gАР0 /R. С учетом таких граничных условий становится ясно, что и в объеме поры давление на фронте волны изменяется по гармоническому закону. Тогда получим для него простое дифференциальное уравнение 2-го порядка по у: 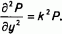
Его решение следующее: P = Р1* ехр(ky) + Р2 ехр(-ky). Постановкой данного выражения в граничные условия для давления находим:
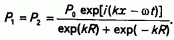
В итоге для давления Р в полуограниченной области х >=0, -R <=у <= R получим следующее решение уравнения Лапласа из системы (8):
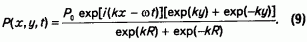
Решение задачи для продольной компоненты скорости при добавлении начального условия u(х,у,0)=0 ищем в виде ряда
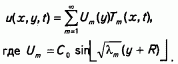
Из граничного условия для продольной компоненты скорости находим
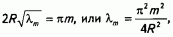
где m = 1, 2, 3 ... Условие нормировки 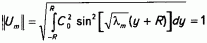 дает нам коэффициент C0 = R1/2. Правую часть первого уравнения системы (8) представим в виде
дает нам коэффициент C0 = R1/2. Правую часть первого уравнения системы (8) представим в виде
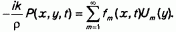
Откуда
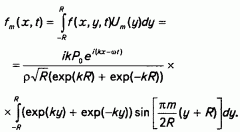
Интеграл в правой части этого уравнения разбивается на два:
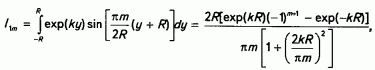
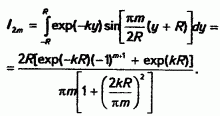
Обозначим
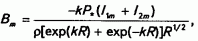
тогда будем иметь

Подставив fm в исходное уравнение, т.е. правую часть первого уравнения (8), получаем уравнение для функции Tm(x,t):
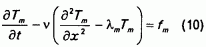
и граничное условие Тm(х, 0) = 0. Для нахождения Тm(х, t) воспользуемся преобразованием Лапласа
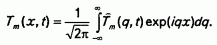
Для 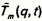 будем иметь задачу
будем иметь задачу
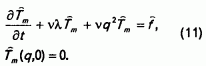
Найдем
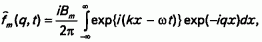
или после интегрирования
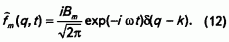
Таким образом, получилось следующее уравнение для нахождения 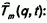
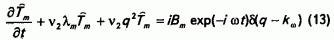
с начальным условием 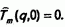
Решение данной задачи:
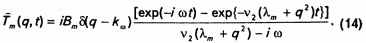
Отсюда с помощью обратного преобразования Лапласа
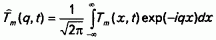
получим
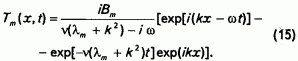
Отбрасывая мнимую часть Тm(х,t) и подставляя значение многочлена в ряд
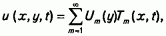
получим окончательно для продольной компоненты скорости [5]
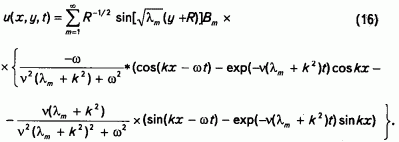
Интегрируя (16), легко получить выражение для смещения S
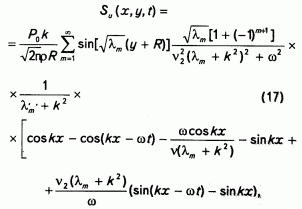
из которого, учитывая типичные значения входящих в (17) параметров горных пород и упругих волн - w = 104с-1, с = 2*103м/с, R=5*10-6 м, m=2*10-2 кг/мс, r=103 кг/м3 (так как k = w/c), получим зависимость смещения от упомянутых параметров, идентичную (2).
Таким образом, приходим к выводу, что течение в плоском прямолинейном поровом канале носит существенно одномерный характер. Случай искривленного порового канала требует отдельного рассмотрения, но ясно, что извилистость пор становится значительной при выходе процесса фильтрационных перетоков из режима Дарси, в противном случае в общие тенденции развития данного процесса, инициируемого упругой волной, необходимо лишь внести поправки инерционного характера.
Теоретические основы методики определения проницаемости горных пород требуют экспериментального подтверждения. Лабораторные эксперименты по количественной оценке эффекта обратной корреляции скорости распространения продольных волн в пористых проницаемых породах с интенсивностью упруго-волнового воздействия были проведены на стандартной установке ИФЕС-1. Данная установка предназначена для измерения упругих и электрических параметров горных пород, на ней возможно регулирование таких внешних факторов, как температура, обжимающее и поровое давления и т.д., что моделирует условия проведения эксперимента на большом интервале глубин [3].
Для экспериментов были использованы технологический блок и стандартная аппаратура для определения времени распространения продольной волны в образцах. Технологический блок состоит из двух гидробарокамер, двух пресс-измерителей для регулировки внутрипорового давления, насоса высокого давления, системы нагрева с терморегулировкой, гидросистем для создания давления обжима образца и внутрипорового давления. В качестве кернодержателей используются верхние пробки гидробарокамер, в которых размещены пьезоэлектрические преобразователи из пьезокерамики марки ЦТС-19.
Аппаратура, используемая для измерения времени распространения продольной волны в образцах, включает измеритель временных интервалов И2-26. усилители зондирующих импульсов, усилитель сигнала приемника и пьезокерамические преобразователи. Принцип работы состоит в следующем. Опорные импульсы, сформированные источником временных сдвигов (ИВС) измерителя И2-26 с частотой 25-600 кГц, поступают на вход усилителя опорных импульсов, усиливаются на амплитуде до 1000 В и подаются на пьезокерамический излучатель, где преобразуются в акустические колебания. Пройдя через образец, акустические колебания поступают на пьезоэлектрический приемник, где преобразуются в электрический сигнал, который усиливается и подается на вход индикатора И2-26. На экране электронно-лучевой трубки индикатора при этом наблюдается волновая картина принятого сигнала. Изменяя на ИВС время задержки между опорными и задержанными импульсами и совмещая таким образом начало принимаемого сигнала с началом развертки, определяют время распространения упругих продольных колебаний в образце.
Предварительные эксперименты, в которых амплитуда воздействия изменялась от 20 до 100 В, показали возможность существования эффекта фильтрационных перетоков (Халилов В.Ш., Антонов К.В., Бандов В.П. и др., 1999). Нижний предел амплитуды возбуждения был принят равным 20 В после оценки допустимых погрешностей и для достижения необходимой надежности измерений. Изменение кинематических параметров волны достигало 2 %, при этом имело место монотонное увеличение скорости продольных волн. Однако позже было отмечено, что режим работы излучателя при максимальных значениях амплитуды упругой волны становился существенно нелинейным. Эти аппаратурные недостатки были устранены.
Дальнейшая оптимизация экспериментального оборудования привела к увеличению максимальной амплитуды излучаемых импульсов со 100 до 1000 В. Это было достигнуто с помощью дополнительно разработанного генератора возбуждения, переключаемого на пьезоэлектрический излучатель. Таким образом, фактический диапазон изменения амплитуд излучаемого импульса составил от 20 до 1000 В и практически сравнялся с таковым в скважинной аппаратуре АК. С целью минимизации влияния частотно-фазовых искажений в указанном сдвоенном диапазоне изменения амплитуд излучаемых импульсов временные измерения осуществлялись по экстремальной (максимальной по амплитуде) фазе первого вступления нормализованной по амплитуде продольной волны, принятой приемником.
Для лабораторных исследовании было отобрано 12 образцов терригенных и карбонатных пород с месторождений различных нефтеносных регионов России, характеризующихся широким диапазоном изменения фильтрационно-емкостных свойств пористости от 0,5 до 25,0 %, проницаемости от 0 до 1 мкм2 (Халилов В.Ш., Антонов К.В., Бандов В.П., 1999, [4]). Непосредственно перед измерениями акустических свойств образцы насыщались минерализованной водой, имитирующей пластовую. Кроме образцов стандартных размеров диаметром 30 мм и высотой 30 40 мм, исследовались крупногабаритные образцы и модели пористых пород. Проницаемые образцы карбонатных пород представлены крупнопористым, частично мелкокавернозным доломитом с Центрально-Талаканской площади. Диапазон проницаемости - (47-227)*10-3 мкм2, пористости -13,5-18,5 %. В качестве слабопроницаемых образцов были взяты плотный, тонкозернистый известняк с Грунташевской площади и ангидрит с трещиной вдоль напластования, частично выполненной гипсоангидритом, с Николашкинской площади, характеризующиеся проницаемостью (0-0,04)*10-3 мкм2, пористостью 0,44-4,20 %. Проницаемые образцы терригенных пород - кварцевый песчаник со Средне-Ботуобинской площади. Диапазон проницаемости - 0,8-1,0 мкм2, пористости - 14-25 %. Непроницаемые образцы представлены плотно сцементированным кварцевым песчаником с Таас-Юрахской площади.
Для учета общей инструментальной погрешности, изменяющейся за счет совокупности различных (статических, динамических) задержек, использовались разноскоростные эталоны из монолитных непроницаемых материалов - плексигласа и стали, охватывающие крайние границы реального диапазона скоростей (2-6 км/с). В качестве эталонов можно также использовать плотные непроницаемые образцы горных пород. Для получения приращений Dt, свободных от влияния различных искажающих факторов, из значений приращений, полученных на проницаемых образцах, вычитались значения приращений, полученные на эталонах.
Под относительным приращением Dt понималась разница между приращениями в проницаемых и непроницаемых образцах, приведенными к одной высоте, выраженной в процентах. Данная величина наиболее однозначно в количественном отношении характеризует исследуемый эффект.
Из рис. 2 видно, что для весьма больших значений проницаемости песчаников (образцы 3 и 4) интервальное время распространения волны зависит от амплитуды нелинейно и достигает максимальных значений соответственно 1,5 и 2,0 % при напряжении питания U генератора импульсов ~400 В. При дальнейшем увеличении U значение приращений Dt резко снижается и при U = 800 В стабилизируется на уровнях 0,65 и 0,85 % для образцов 3 и 4 соответственно. Для карбонатных пород ( рис. 3 ) характер зависимостей в целом аналогичен таковому для песчаников (см. рис. 2 ), однако из-за меньшей их проницаемости здесь получаются соответственно меньшие приращения Dt - в основном 0,65 %. И лишь в самом высокопроницаемом (Kпр = 0,3 мкм2) образце доломита 5 приращение Dt при U = 400 В достигает 1,55 %.
Следующий этап лабораторных исследований проводился на блоке естественного известняка с пористостью 38 %, проницаемостью 0,2 мкм2, выполненном в виде прямоугольника с размерами 160x160x400 мм, и моделях искусственных песчаников цилиндрической формы диаметрами 30-150 мм и высотой 40-400 мм с пористостью 33,7-34,6 %, проницаемостью (240-422)*10-3 мкм2. В ходе измерений кинематических характеристик упругих волн на таких образцах было установлено отсутствие влияния на них рабочих частот в диапазоне 25-600 кГц, размеров образцов и гранулометрического состава.
Полученные результаты на частично водонасыщенном образце сравнимы с таковыми на плотных, непроницаемых образцах. Если взять для сравнения результаты, полученные на доломите и водонасыщенном известняке, характеризующихся одной и той же проницаемостью 0,2 мкм2 в диапазоне амплитуды 200-700 В, то они достаточно близки, хотя по пористости эти образцы отличаются в 2 раза.
Графики на рис. 4 представляют зависимости относительного приращения Dt от амплитуды упругого импульса в диапазоне от 100 до 1000 В, полученные для моделей искусственных песчаников. Данные песчаники пористостью 33,7-34,6 % и проницаемостью (240-422)*10 -3 мкм2 были изготовлены из смеси кварцевого песка и тампонажного цемента по следующей методике. Сначала готовилась смесь, состоящая из 12 % цемента, 88 % отсортированного песка с размерами зерен 0,2 мм и воды, количество которой составляло 40 % общего объема смеси. Затем эта смесь заливалась в цилиндрические формы и оставлялась в воздушной среде на две недели до полного отвердения. После этого готовые образцы помещались в воду на 1.5 мес., в течение которых упругие свойства песчаников стабилизировались. Характер зависимостей для искусственных образцов в целом аналогичен таковому для кварцевых песчаников (см. рис. 2 ). Относительное приращение Dt достигает максимума при амплитуде U = 400 В, а при дальнейшем увеличении U Dt снижается. Рассматривая графики по образцам 15 и 17 с проницаемостью 0,4 и 0,24 мкм3 соответственно, видим, что они заметно отличаются по величине приращения Dt - соответственно 2,3 и 1,3 при U = 400 В. Если учесть, что эти образцы одинакового размера, имеют одинаковую гранулометрическую характеристику и близки по пористости (33,7 и 34,6 % соответственно), то можно с большой уверенностью сказать, что приращение Dt в данном случае контролируется проницаемостью, причем различие в приращении в 1,8 раза пропорционально различию проницаемости в 1,76 раза.
Таким образом, по результатам анализа семейства полученных зависимостей выявляется наличие эффекта снижения скорости продольных волн от интенсивности упруговолновых воздействий на проницаемую породу, причем максимальное проявление эффекта наблюдается лишь при определенной интенсивности (U = 400 В). Однако называть ее оптимальной еще преждевременно, так как требуется достоверное теоретическое обоснование.
В целом эксперименты подтвердили верность теоретических предпосылок, а именно, гипотезы об эффекте фильтрационных перетоков. Модельные представления пористой среды в виде совокупности прямолинейных поровых каналов показали возможность получения зависимостей между параметрами пористой среды и характеристиками упругих волн. Это относится в основном к высоко- и среднепроницаемым образцам песчаника, причем для искусственно созданных образцов песчаника полученные зависимости проявляются наиболее четко. Это дает основания полагать, что упругие свойства горных пород подвержены изменению, обусловленному непрерывным осадконакоплением. Что касается относительно малопроницаемых образцов, например образцов карбонатных пород 13 и 14, то здесь не все так однозначно. Ввиду малости их фильтрационно-емкостных параметров, а, следовательно, малого содержания жидкости, влияние последней на характеристики упругой волны минимально. Видимо, в таких случаях первостепенными становятся свойства твердого скелета, отклик которого на упруговолновое воздействие может быть рассчитан при рассмотрении совершенно иных моделей горных пород. Свойства таких моделей будут очень близки к свойствам сплошного твердого тела, деформация которого является упругой и в значительной степени подчинена закону Гука. Объяснение наличия максимума относительного приращения времени распространения продольных волн на представленных графиках требует проведения дополнительных теоретических исследований.
По результатам анализа погрешностей лабораторных исследований взаимосвязей акустических и фильтрационно-емкостных свойств уточнены требования к технике и методике измерений. Проведены необходимые усовершенствования, позволившие повысить точность лабораторных измерений кинематических параметров продольных волн до 0,10-0,15 %. Результаты обобщения лабораторных исследований подтверждают наличие эффекта снижения скорости акустических продольных волн с частотой 500 кГц до 2 % в пористых проницаемых породах при 10-кратном увеличении амплитуды акустического воздействия. Установленная нелинейная зависимость данного эффекта от амплитуды возбуждаемого упругого импульса использована для оптимизации режимов возбуждения сейсмоакустических источников в аппаратуре акустического каротажа и межскважинного сейсмопросвечивания (сейсмотомографии), с помощью которых предусматривается практическое применение разрабатываемой методики оценки проницаемости пластов в скважинах.
Литература
Abstract
A possibility of evaluating filtration characteristics of rocks using longitudinal waves is considered in the article. To confirm theoretical bases of the method for determining rocks permeability there have been performed the laboratory experiments for quantitative evaluation of the effect of reverse correlation of longitudinal wave propagation velocity in porous permeable rocks depending on elastic wave effect intensity. The presence of the effect of longitudinal wave velocity decrease depending on the value of elastic wave intensity upon permeable rocks was revealed. As a whole, experiments demonstrated the correctness of theoretical hypotheses about filtration crossflow effect. Modeling of porous medium as a set of rectilinear pore channels showed a possibility to obtain relationships between porous medium and elastic wave characteristics.
Рис. 1. ПЛОСКАЯ ГИДРОДИНАМИЧЕСКАЯ МОДЕЛЬ ПОРОВОГО ПРОСТРАНСТВА
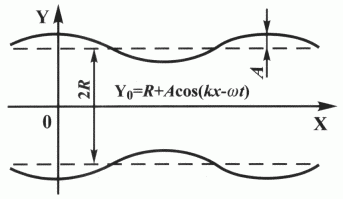
R - радиус поры; А - амплитуда смешения границы порового канала
Рис. 2. ЗАВИСИМОСТЬ ОТНОСИТЕЛЬНОГО ПРИРАЩЕНИЯ ВРЕМЕНИ РАСПРОСТРАНЕНИЯ ПРОДОЛЬНЫХ ВОЛН В ОБРАЗЦАХ ПЕСЧАНИКОВ ОТ АМПЛИТУДЫ ИЗЛУЧАЕМЫХ ИМПУЛЬСОВ
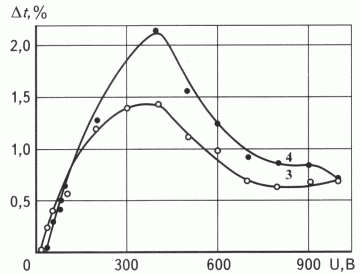
Проницаемость и пористость для образцов 3 и 4 соответственно 0,8; 1,0 мкм2 и 14,0; 25,1 %
Рис. 3. ЗАВИСИМОСТЬ ОТНОСИТЕЛЬНОГО ПРИРАЩЕНИЯ ВРЕМЕНИ РАСПРОСТРАНЕНИЯ ПРОДОЛЬНЫХ ВОЛН В ОБРАЗЦАХ КАРБОНАТОВ ОТ АМПЛИТУДЫ ИЗЛУЧАЕМЫХ ИМПУЛЬСОВ
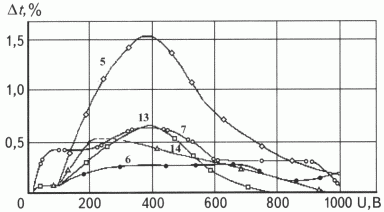
Проницаемость и пористость для образцов 5, 6, 7, 13, 14 соответственно 0,227; 0,053; 0,196; 0,059; 0,047 мкм2 и 13,5; 13,5; 14,4, 18,5; 14,0 %
Рис. 4. ЗАВИСИМОСТЬ ОТНОСИТЕЛЬНОГО ПРИРАЩЕНИЯ ВРЕМЕНИ РАСПРОСТРАНЕНИЯ ПРОДОЛЬНЫХ ВОЛН В МОДЕЛЯХ ИСКУССТВЕННЫХ ПЕСЧАНИКОВ ОТ АМПЛИТУДЫ ИЗЛУЧАЕМЫХ ИМПУЛЬСОВ
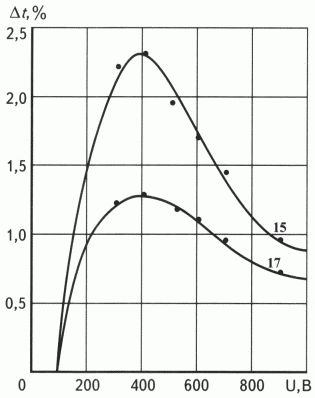
Проницаемость и пористость для образцов 15 и 17 соответственно 0,422; 0,240 мкм2 и 33,7, 34,6%