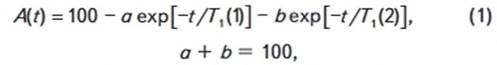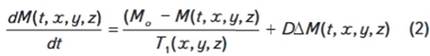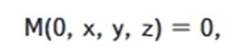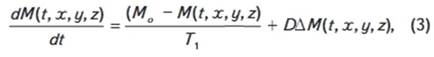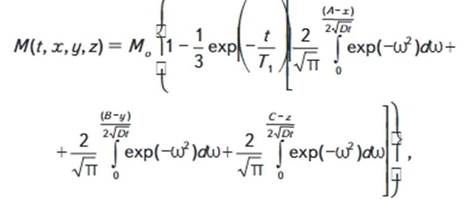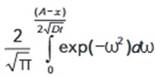Библиотека Дамирджана - Геология нефти и газа - 2003

РЕЛАКСАЦИОННЫЕ ХАРАКТЕРИСТИКИ ВОДЫ В ПОРОВОМ ПРОСТРАНСТВЕ КОЛЛЕКТОРОВ НЕФТИ И ГАЗА

В.А. Сафин, С.Е. Войтович (ТГРУ ОАО “Татнефть")

Метод ядерного магнитного резонанса (ЯМР) применяется при определении коллекторских свойств горных пород и насыщающих их флюидов [3, 4]. Метод особенно эффективен при исследовании водонефтенасыщенного керна, так как он позволяет определять свойства жидкостей непосредственно в поровом пространстве, без нарушения структуры и целостности образца. Сложность метода заключается в соотнесении получаемых при разложении компонент релаксационных кривых и соответствующих фаз нефти и воды, поскольку нефть является многокомпонентной и вода в поровом пространстве в отличие от свободного объема оказывается также многокомпонентной [3, 4]. Сложность соотнесения усугубляется неоднозначной интерпретацией различными авторами многокомпонентности релаксационной кривой, описывающей спин-решеточную (спин-спиновую) релаксацию воды в поровом пространстве.

В [2, 3] придерживаются модели, согласно которой фаза жидкости с более коротким временем релаксации соответствует молекулам воды, находящимся в мелких порах, с длинным временем релаксации - молекулам воды в более крупных порах. При допущении заполнения пор одинаковой жидкостью и сходства свойств поверхности пор распределение времен релаксации характеризует распределение размера пор в образце.

В [5] предлагается иная модель состояния жидкости в поровом пространстве. Жидкость в поре имеет две области с различной подвижностью: первая соответствует области, сопряженной с поверхностью, вследствие чего ограничивается подвижность молекул воды, а наблюдаемое время релаксации мало; вторая соответствует области срединной части поры, где подвижность молекул воды также ограничена, но в то же время больше подвижности молекул первой области, а наблюдаемое время релаксации больше такового для воды первой области.

В описанных выше 1-й и 2-й моделях не рассматриваются механизмы влияния поверхности поры на состояния воды в поровом пространстве. Из экспериментов, приведенных в [2-5], следует, что влияние поверхности достигает толщины воды порядка нескольких тысяч монослоев. Трудно представить механизм, ограничивающий подвижность молекул воды поверхностью на расстояние порядка нескольких тысяч ангстрем, исходя из известных типов молекулярных связей. Целью данной статьи является объяснение многокомпонентности релаксационной характеристики воды в поровом пространстве, установление связи релаксационных характеристик с параметрами структуры порового пространства и свойствами насыщающих его жидкостей.

Для исследований были подготовлены три модельных образца, представляющих собой измерительную пробирку с дистиллированной водой (время спин-решеточной релаксации Т₁ = 2,2 с), в которую засыпался некоторый объем (8 см³) зерен молотого кварца определенной фракции. Разделение на фракции производилось с помощью сит с классом крупности -0,064...+0,05; -0,1...+0,064 и -0,2...+0,16 (средний размер зерен 57; 82 и 180 мкм). Образцы перед измерением прокаливались при температуре 300 °С в течение 4 ч и выдерживались 2 сут.

Измерения релаксационных характеристик состояния воды в модельных образцах проводились на импульсном ЯМР-спектрометре фирмы BRUKER mq10 на частоте 10 мГц при помощи импульсной последовательности 90° - t- 90° -. Релаксационные кривые с высокой точностью описываются функцией вида

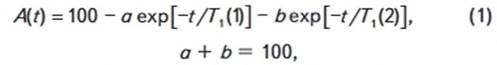
где а, b - процентные доли компонент; T₁(1), T₁(2) - времена спин-решеточной релаксации компонент. Из результатов измерений времени спин-решеточной релаксации (рис. 1) и коэффициентов a и b (рис. 2) для модельных образцов следует, что с уменьшением среднего размера зерен времена релаксации компонент воды в поровом пространстве уменьшаются, причем длинновременная компонента Т₁(1) сокращается сильнее, чем коротковременная компонента Т₁(2). Заметим, что размер пор модельных образцов связан с размером зерен фракции: чем больше размер зерна, тем больше размер поры. Полученные нами результаты совпадают с результатами из работ (Тульбович Б.И., 1990; [2-5]), причем в работах (Тульбович Б.И., 1990; [4]) приведены данные измерений в модельных образцах, состоящих из стеклянной и мраморной крошки, песка, силикагеля, фторопласта различных геометрических форм. Во всех моделях независимо от геометрии пор и физико-химических свойств поверхности релаксационные характеристики воды отличны от релаксационных характеристик воды в свободном объеме. В некоторых моделях наблюдается двухфазное состояние воды, объясняемое тем, что молекулы воды могут быть как сильно (пристеночный слой), так и слабо связаны с поверхностью.

Исходя из 1-й модели наблюдаемые нами результаты интерпретируются следующим образом: в образцах 20-25 % воды находятся в мелких порах, а остальная часть - в более крупных порах, т.е. в образцах поры имеют два средних размера. Таким образом, наблюдается двухмодальное распределение пор в исследуемых образцах.

В соответствии с 2-й моделью образцы обладают порами одного характеристического размера, причем вода находится в порах в двух фазах. Первая фаза, с коротким временем релаксации (пристеночная вода), занимает 20-25 % объема поры, вторая, с длинным временем релаксации, занимает срединную часть объема поры, причем переход между фазами неплавный.

Границу между фазами можно определить при допущении формы поры. В случае сферической формы поры с радиусом R граница находится на расстоянии (0,93- 0,90)*R. В наших модельных образцах воздействие поверхности распространяется на расстояние порядка 10 000 монослоев при R= 50 мкм.

Отметим, что времена релаксации воды в 1-й и 2-й моделях оказываются короче времени релаксации для воды свободного объема. Поскольку вода находится в поре, то уменьшение времени релаксации объясняется воздействием поверхности поры на подвижность молекул воды. В соответствии с представлениями о релаксации в жидкости [1] времена релаксации определяются подвижностью молекул воды. Из теории следует, что молекулы воды с более коротким временем релаксации обладают меньшей подвижностью. Получается, что вода в 1-й и 2-й моделях находится в заторможенном состоянии.

Для проверки факта заторможенного состояния воды во внутрипоровом пространстве были проведены измерения коэффициентов самодиффузии в модельных образцах. Измерения коэффициентов самодиффузии проводились методом импульсного градиента магнитного поля на импульсном ЯМР-спектрометре фирмы BRUKER mq10 на частоте 10 мГц при помощи импульсной последовательности 90° - т - 180° -. В табл. 1 приведены результаты измерений для образца с классом крупности - 0,64...+0,50.

На рис. 3 приведен график зависимости логарифма отношения сигнала эхо с градиентом магнитного поля к сигналу без градиента магнитного поля от квадрата градиента магнитного поля (график Стейскала-Таннера). Из прямолинейного характера графика следует, что подвижность воды в образце определяется одним коэффициентом самодиффузии, причем среднее значение коэффициента самодиффузии равно 2,24 • 10 ^-5 см² • с^-1. Данное значение соответствует коэффициенту самодиффузии воды при температуре 24 °С. Из изложенного следует, что вода в порах исследуемого образца имеет подвижность воды свободного объема.

Для объяснения двухфазного состояния воды в поровом пространстве предлагается следующая модель: поверхность поры оказывает воздействие на молекулы воды, находящиеся вблизи стенки (пристеночная вода), достигая толщины 3-4 монослоев, остальная вода имеет свойства воды свободного объема (свободная вода). Между пристеночной и свободной водой происходит диффузионный обмен. Развитие намагниченности (М) воды внутри поры в предлагаемой модели описывается уравнением

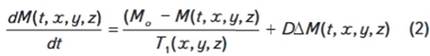
с начальными условиями

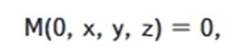
где М₀ - равновесное значение намагниченности в поре; Т₁(х, у, z) - время спин-решеточной релаксации компонент воды; D- коэффициент самодиффузии; Δ- оператор Лапласа.

Первый член правой части уравнения (2) ответственен за восстановление намагниченности после воздействия 1-го 90-градусного импульса за счет спин-решеточной релаксации, второй член - за процесс диффузии. Начало развития намагниченности отсчитывается по окончанию воздействия 1-го 90-градусного импульса. Решение уравнения (2) в общем виде носит чрезвычайно сложный характер и возможно лишь численными методами. В настоящее время в теоретической физике не устоялись воззрения на вид T₁(x, у, z). Однозначно установлено, что на границе раздела твердое тело - вода значение Т₁(х, у, z) очень мало по сравнению с Т₁(х, у, z) для воды в срединной части поры, так как релаксационные характеристики пристеночной воды будут определяться механизмами релаксации спинов воды вблизи парамагнитных центров, каковыми являются не скомпенсированные по заряду молекулы стенки [1]. Зависимость T₁(x, у, z) от расстояния до стенки разными авторами оценивается по-разному - от r³ до r⁶. Для нас важно, что переход очень резкий. Таким образом, намагниченность пристеночной воды восстанавливается до равновесного значения за очень короткое время, а намагниченность свободной воды восстанавливается за счет времени спин-решеточной релаксации и процесса диффузии, т.е. за счет более длинновременных процессов. Это позволяет упростить ситуацию и рассмотреть уравнение развития намагниченности для свободной воды, приняв толщину пристеночной воды равной одному монослою, намагниченность которой на начало рассмотрения равна равновесной, а время релаксации пристеночной воды равно нулю. Тогда уравнение (2) примет вид

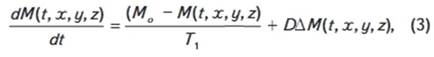
где Т₁ - время спин-решеточной релаксации свободной воды, с начальными условиями на границе поры

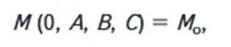
где А, В, С - граничные значения переменных х, у, z, с начальными условиями внутри поры

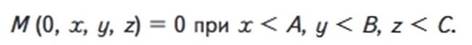
Решение уравнения (3) для параллелепипедной формы поры в декартовой системе координат имеет следующий вид

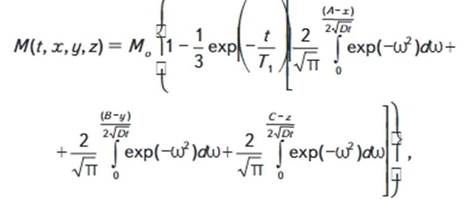
где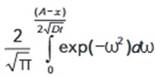- интеграл вероятности ошибок.

Намагниченность воды для всей поры, нормированная на объем поры, равна

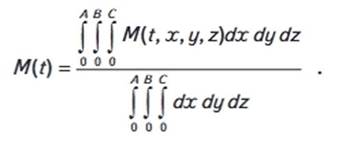
На компьютере вычислялись значения M(t) при D= 2,04*10^-5 см² *с^-1 при температуре 20 °С [1], Т1 = 2,2 с и при различных значениях А, В, С. Полученные табличные значения M(t) аппроксимировались уравнением (1). Методом наименьших квадратов находились значения параметров а, b, T₁(1) и T₁(2). На рис. 4 показан пример сопоставления значений M(t) и A(t) при А = В = C= 50 мкм.

В табл. 2 приведены значения параметров а, b, T₁(1) и T₁(2) при фиксированных значениях А, В, С, причем для иллюстрации принято А = В = С, пора выбрана в форме куба.

На рис. 5 и 6 приведены графики зависимостей значений параметров T₁(1), T₁(2) и а, b соответственно от величины, составляющей половину длины ребра куба (размер поры).

Полученные релаксационные характеристики воды в поровом пространстве на основе предлагаемой модели качественно сопоставимы с релаксационными характеристиками модельных образцов (см. рис. 1, 2). Релаксационная кривая распадается на две компоненты, зависимости поведения параметров T₁(1), T₁(2) и a, b от размера пор имеют одинаковый характер. Расхождение в количественных оценках релаксационных характеристик обусловлено несоответствием геометрии пор модельных образцов геометрии куба.

The purpose of investigation data is to find out the relationship of characteristic relaxation state of water in porous medium with parameters of porous medium structure and properties saturating liquids. To achieve the desired target, the model of water consisting of wall water in 1 monolayer and free water thick between which occurs the diffusion exchange was proposed. Numeric mathematic modelling of dynamic processes on the basis of proposed model allowed to explain two-component nuclear magnetic relaxation of water within intraporous medium observed in experiment.

Литература

1. Вашман А.А., Пронин И.С. Ядерная магнитная релаксация и ее применение в химической физике. - М.: Наука,1979.

2. Определение коллекторских свойств горных пород импульсным методом ядерного магнитного резонанса (Методические рекомендации) / Сост. В.Д. Неретин, Я.Л. Белорай, В.Н. Чижик и др. - М.: ВНИИЯГГ, 1978.

3. Применение ЯМР в нефтяной геологии / Р.Х. Муслимов, С.Н. Головко, Т.А. Захарченко, Н.Л. Захарченко. - Казань, 1998.

4. Тульбович Б.И. Методы изучения пород-коллекторов нефти и газа. - М.: Недра, 1979.

5. Seevers D.O. Nuclear magnetic method for determining the permeability of sandstones // Trans. SPWLA. - 1966. - Vol. 138. - P. 682-687.

Таблица 1

Градиент (G), Тл/м	G², (Тл/м)²	Амплитуда сигнала с градиентом (A_i), %	Амплитуда сигнала без градиента (A₀), %	ln(Ai/A₀), %	Коэффициент диффузии, n*10^-9 м²/с
0,56777	0,322363	64,99	66,83	-2,7919	2,28150
0,86690	0,751516	62,28	66,39	-6,3906	2,23850
1,05050	1,103550	60,50	66,52	-9,4800	2,23690
1,16610	1,359789	58,81	66,50	-12,2890	2,21274

Таблица 2

А, B, C, мкм	а, %	T₁(1), мс	b, %	T₁(2), мс
25	61,756	39	38,233	740
50	47,953	94	52,037	1067
75	36,812	131	63,177	1239
100	28,006	135	71,982	1353
150	17,527	133	82,459	1531
200	12,929	135	87,057	1671
300	8,950	143	91,036	1850

Таблица 3

R, мкм	а, %	Т₁(1), мс	b, %	T₁(2), мс
25	64,321	16	35,667	476
50	53,885	41	46,103	802
75	44,225	60	55,764	959
100	38,368	78	61,620	1122
150	29,105	99	70,883	1322
200	23,240	111	76,746	1464
300	16,624	126	83,363	1655

Рис. 1. ЗАВИСИМОСТЬ ВРЕМЕН СПИН-РЕШЕТОЧНОЙ РЕЛАКСАЦИИ КОМПОНЕНТ ВОДЫ ОТ СРЕДНЕГО РАЗМЕРА ЗЕРЕН МОДЕЛЬНЫХ ОБРАЗЦОВ

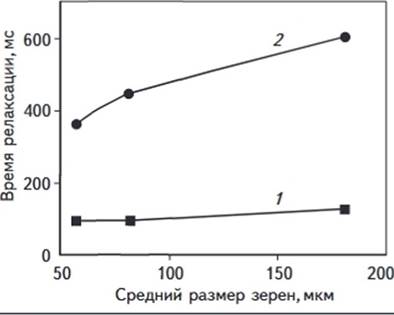
Время спин-решеточной релаксации компонент воды: 1 -Т₁(1), 2-Т₁(2)

Рис. 2. ЗАВИСИМОСТЬ ПРОЦЕНТНЫХ ДОЛЕЙ КОМПОНЕНТ ВОДЫ ОТ СРЕДНЕГО РАЗМЕРА ЗЕРЕН МОДЕЛЬНЫХ ОБРАЗЦОВ

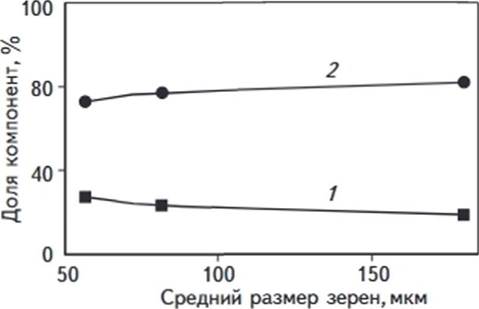
Процентная доля компонент йоды: 1 а, 2 b

Рис. 3. ГРАФИК СТЕЙСКАЛА-ТАННЕРА

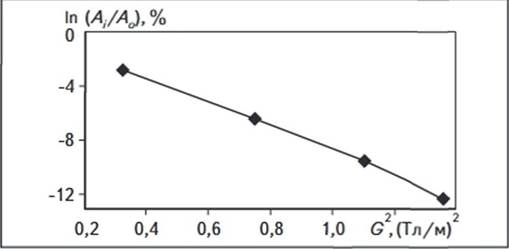
Рис. 4. ГРАФИКИ ЗАВИСИМОСТИ M(t) И A(t) ОТ ВРЕМЕНИ РАЗВИТИЯ НАМАГНИЧЕННОСТИ

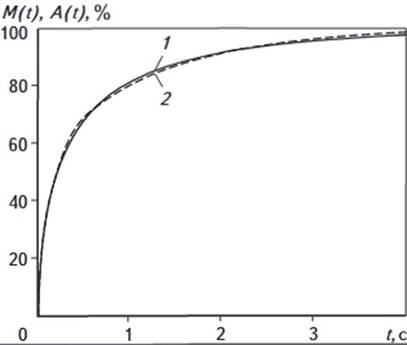
1 M(t); 2 A(t); a = 47,953 %; b = 52,037 %; T₁(1) = 0,094 с; T₁(2) = 1,067 c

Рис. 5. ЗАВИСИМОСТЬ ВРЕМЕН СПИН-РЕШЕТОЧНОЙ РЕЛАКСАЦИИ КОМПОНЕНТ ВОДЫ ОТ РАДИУСА ПОР

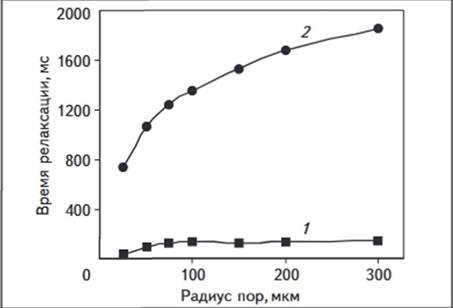
Усл. обозначения см. на рис. 1

Рис. 6. ЗАВИСИМОСТЬ ПРОЦЕНТНЫХ ДОЛЕЙ КОМПОНЕНТ ВОДЫ ОТ РАДИУСА ПОР

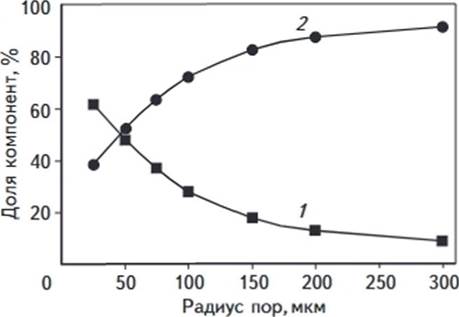
Уел. обозначения см. на рис. 2

Рис. 7. ЗАВИСИМОСТЬ ВРЕМЕН СПИН-РЕШЕТОЧНОЙ РЕЛАКСАЦИИ КОМПОНЕНТ ВОДЫ ОТ РАДИУСА ПОР

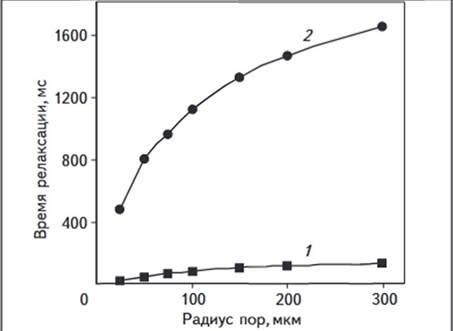
Усл. обозначения см. на рис. I

Рис. 8. ЗАВИСИМОСТЬ ПРОЦЕНТНЫХ ДОЛЕЙ КОМПОНЕНТ ВОДЫ ОТ РАДИУСА ПОР

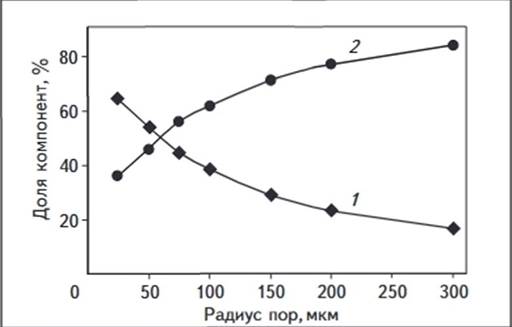
Усл. обозначения см. на рис. 2