К оглавлению

© Коллектив авторов, 2004

ОЦЕНКА ПОТЕНЦИАЛЬНЫХ РЕСУРСОВ УГЛЕВОДОРОДОВ ГЕОМАЯТНИКОВЫМ МЕТОДОМ (на примере Тимано-Печорской провиниии)

С.Л. Садов, Б.И. Тарбаев (ИСЭПС Коми НЦ УрО РАН), В.В. Иванов, Н.И. Кузнецов (ООО “Севергазпром”)

Промышленному освоению нефтегазоносных провинций предшествуют оценки потенциальных ресурсов, величины которых предопределяют масштабы и темпы проведения геолого-разведочных работ и от чьей достоверности в решающей степени зависит экономическая эффективность инвестирования средств в освоение нефтегазовых ресурсов.

На ранних этапах, когда объем информации о нефтегазоносности относительно невелик, оценка перспектив провинции и ее частей выполняется традиционным способом. С этой целью используются несложные, но требующие опыта и знаний трудоемкие методы, результаты которых кладутся в основу поисковых стратегий и последующих работ, связанных с эксплуатацией открытых месторождений. В то же время очевидно, что даже самый тщательный анализ имеющейся информации и высокая квалификация исполнителей в ситуации полной или частичной неопределенности, продиктованной уровнем знаний о провинции, не предохраняют от больших ошибок, и в этой связи для инвестора всегда существует риск получить прибыль, меньшую ожидаемой, или понести убытки. Объемы начальных суммарных ресурсов (НСР) на ранних стадиях освоения нефтегазоносных регионов - это ориентировочные величины. Поэтому на последующих стадиях, когда территория уже покрыта сетью сейсморазведочных профилей, а на выявленных объектах пробурены скважины и подсчитаны промышленные запасы, возникает необходимость корректировки потенциальных ресурсов. Корректировка первоначальных величин НСР - это естественный процесс, который стимулируется как фактором снижения открываемости залежей при высокой степени опоискованности территории, так и большим остаточным ресурсным потенциалом. Нередко возникает парадоксальная ситуация, когда при большом дефиците объектов для постановки поискового бурения остаток НСР может превышать половину и более их начальной величины.

В случае, когда степень опоискованности территории достаточно высока, используются численные методы, реализованные в виде специальных алгоритмов, в основу которых положены математические принципы, адекватно описывающие геологические ситуации. При этом эффективность численных методов находится в прямой зависимости от накопленной информации, определяющей уровень неопределенности. При достижении стадии, характеризующей исследовательскую зрелость, они позволяют получать заслуживающие доверия результаты. Так, геомаятниковый метод, разработка которого велась европейскими и американскими специалистами в 80-90-х гг. XX в., является одной из самых оригинальных методических разработок в области оценки ресурсного потенциала нефтегазоносных регионов [3]. Авторы настоящей статьи не сразу нашли подходящий перевод названия метода (Geo-anchored method). Буквальный перевод - “геоякорный” - по нашему мнению, механистичен и не отражает сущности метода, тогда как “геомаятниковый” вполне отвечает его духу, затуханию величин погрешностей по мере роста базы для проведения расчетов. Что касается области его применения, то при соответствующей доработке она представляется существенно более широкой - оценкой перспектив использования любого ограниченного ресурса, что открывает возможности использования метода в экономических, экологических, социологических исследованиях.

Геомаятниковый метод - история развития и основное содержание

Основная цель математических процедур - сделать процесс принятия решений в области поисков и разведки более обоснованным. Даже небольшое повышение эффективности здесь очень важно с точки зрения экономики. Предприятие, принявшее решение вложить средства в проекты освоения залежей УВ, имеет в перспективе цепь рисковых ситуаций, которые целесообразно оценить еще до начала реализации проектов.

И первым звеном в этой цепи является риск, связанный с поиском залежей УВ, чреватый в случае неуспеха серьезными финансовыми потерями. Истоки риска лежат в области оценок потенциальных УВ-ресурсов региона, в границах которого планируется провести поисковые работы. Мировая практика не знает случаев, когда потенциальные ресурсы на некоторой территории оценивались бы значительной величиной, а на самом деле равнялись бы нулю. Но немало примеров, когда оценка потенциальных ресурсов от выявленных и разведанных запасов отличалась весьма существенно, иногда на порядки. При этом нет оснований обвинять участвовавших в оценке экспертов в небрежности - методики оценок не гарантируют от ошибок.

На ранних стадиях освоения нефтегазоносных бассейнов (НГБ) ошибки в оценках начальных потенциальных ресурсов не имеют серьезных последствий, поскольку в этот период, как правило, происходит открытие крупных месторождений и поисковые работы окупаются. Иное дело, когда НГБ изучен в достаточной степени, большинство крупных и средних месторождений уже выявлено и речь идет о поисках мелких залежей. Остаток потенциальных ресурсов представляет собой разницу между НСР и выявленными запасами промышленных категорий. И по мере того как увеличивается разведанность территории и возрастает объем запасов, становится все ощутимей погрешность в определении величины НСР. Наступает момент, когда величину остатка будут определять не реально существующие запасы (которые постепенно переходят в выявленные запасы промышленных категорий), а отклонение оценки НСР от истинного значения. И таким образом, остаток потенциальных ресурсов становится все более фиктивной величиной, а инвестиционная активность, базирующаяся на такой оценке, - все более рисковой. По указанным причинам переоценка величины НСР имеет большое значение для снижения первой ступени риска.

Отметим, что проблема надежности численных методов, начиная с момента их появления, привлекает пристальное внимание специалистов, побуждая их к поиску соответствующих критериев. Этот вопрос неоднократно обсуждался в печати и публичных выступлениях (Barouch Е., Chow К., Kaufman G.M., 1985; Forman D.J., Hinde A.L., 1985; Lee P.J., Wang P.C., 1985; Rosen B., 1972; [4]). В конце концов, поиски увенчались успехом: Дж. Кауфман с соавторами (Andreatta G., Kaufman G.M., 1986; Barouch E., Chow K., Kaufman G.M., 1985) в середине 80-х гг. предложили использовать для этой цели специальную операцию, разработанную Д. Горовицем и Д. Томпсоном и получившую название “оценивание чувствительности”. Суть ее в самом общем виде сводится к исследованию устойчивости результатов при расширяющейся выборке с использованием мультивариационного принципа. Известно, что каждый НГБ в процессе промышленного освоения проходит несколько этапов опоискования, завершающихся открытием некоторого числа месторождений. Каждая группа выявленных месторождений по своей сути представляет выборку. Естественно считать, что более многочисленная выборка при оценке ресурсов должна рассматриваться как предпочтительная. Однако, строго говоря, подобное умозаключение не более чем предположение. Изложенные в работе [3] и приведенные ниже обоснования предполагают последовательное вычисление оценок УВ-ресурсов территории по числу находящихся на ней объектов и суммарных их объемов по мере роста выборки и соответствующего анализа поведения сопровождающих вычисления ошибок. Визуализация результатов вычислительных операций выполняется в системе координат “число открытых месторождений - оценка ресурсов” в виде конуса схождения, демонстрирующего постепенное уменьшение ошибок и указывающего тем самым на эффективность метода и его устойчивость.

Понятно, что такие методические исследования не могли быть выполненными на примере некоторой природной совокупности данных, поскольку любая природная совокупность, особенно когда речь идет о УВ-залежах в недрах земли, остается для экспериментатора неизвестной, и проблема сравнения результатов вычислений с конечной величиной остается неразрешимой. В силу этой причины эксперименты выполнялись на моделях, когда конечное число объектов и их суммарная величина были заранее известны.

Методика экспериментов, принципы формализации и основные математические зависимости, применяемые при экспериментах по геомаятниковому методу, достаточно подробно изложены в работе Ж. Чена и Р. Синдинг-Ларсена [3]. Предполагается, что из N залежей в гипотетической нефтегазоносной провинции открыто n месторождений в следующем порядке:  и т.д. Далее будем называть месторождения объектами. Обозначим открытые объекты в порядке их наблюдения как , а  определим как неупорядоченную совокупность U из N объектов. Последовательность величин, характеризующая открытие объектов, рассматривается как последовательность извлечения элементов из конечной совокупности с вероятностью появления, пропорциональной их размеру, без возвращения в изначальную совокупность. Это типичная модель распределения с перестановками в области всех перестановок, входящих в совокупность U. Случайные варианты обозначаются прописной буквой, а их предполагаемые величины - строчной. Вероятность открытия объектов в порядке  имеет вид

где. Предложенная модель последовательности открытия объектов имеет аббревиатуру SS (Successive Sampling). В более общем виде она описывается формулой

где. В выражении (1) используется так называемый параметр открываемости , который в процессе исследования позволяет отразить ситуации, когда вероятность открытия не прямо пропорциональна величине объекта. Параметр  может быть определен, как указывают Дж. Шенмейер и Л. Дрю (1983), в качестве фактора, способствующего открытию или, по терминологии П. Ли и П. Ванга (1985), как параметр изменения размера.

Как было отмечено, разработке геомаятникового метода предшествовало создание маятникового метода и оценивателя Горовица-Томпсона (сокращенно Н-Т Estimator), смысл и содержание которых заслуживают краткого рассмотрения.

Оцениватель Горовица-Томпсона. Пояснения можно начать с того, что создатели “оценивателя” стремились показать, что между числом объектов и суммой выражений существует определенная связь. Логика доказательств сводится к следующему.

Пусть- функция от. Несмещенная оценка суммы есть

Где - инклюзивная вероятность того, что месторождение с номером  окажется среди первых n открытий. Если все элементы конечной совокупности известны априори, имеется возможность вычислить инклюзивную вероятность. Инклюзивная вероятность  может быть аппроксимирована как

где- единственное решение уравнения

Дж. Кауфман, автор маятникового метода, показал, что если параметр  известен априори, а элементы  выстроены в порядке 1, 2, ..., n, то, сумма всех величин объектов, может несмещенно и приближенно оцениваться как

Приближенная несмещенная оценка числа объектоввыражается формулой

Выражения (2) и (3) раскрывают содержание маятникового метода, разработанного Дж. Кауфманом [4]. В этих выражениях использован элемент оценивателя Горовица-Томпсона, что указывает на преемственность этих методов.

Использование маятникового метода для оперативной оценки сумм исследуемых объектов удобно, но нуждается в предварительной оценке неизвестного параметра Чтобы решить эту проблему, необходимо получить от геологов точечную оценку R и N по неполной выборке и выбрать  для использования выражений (2) и (3).

Геомаятниковый метод. Согласно Дж. Кауфману [5] при условии упорядоченной выборки ожидание случайного события  для (n+1)-гo открытия есть

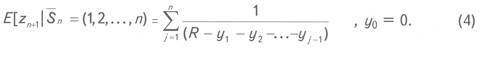
Как только N становится большим и отношение n/N приближается к некой дроби, заключенной между 0 и 1, zn+1 сходится к вероятностидля которой

Ж. Чен [2] установил, что неизвестный параметр  в маятниковом методе может быть аппроксимирован условным ожиданием из выражения (4). Если в формуле (4) заменить реальную величину R ее оценкой из (2), маятниковый метод принимает вид

 

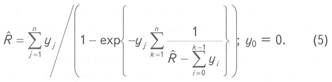
Аналогичное приведенному в выражении (5) решение может быть использовано для оценок числа объектов в конечной совокупности U; оно определяется как

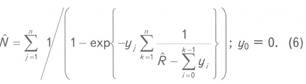
Выражения (5) и (6) характеризуют особенности геомаятникового метода. В общей форме он представляется следующими выражениями:

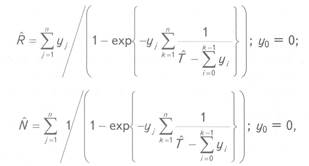
где- единственное решение уравнения

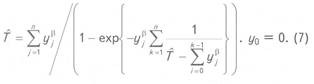
Это решение есть ничто иное как .

При применении геомаятникового метода для оценки R и N главным требованием служит такое упорядочение выборки, когда последняя рассматривается как последовательность величин в порядке их открытия. В этом смысле геомаятниковый метод более чувствителен к исходным данным, чем другие методы. По результатам имитации “открытия” месторождений с различными предположениями относительно эффективности поисково-разведочного процесса, степени “опоискованности” (зрелости, изученности) и вида распределения были выполнены многочисленные расчеты, подтверждающие эффективность метода. Анализ экспериментов показал, что эффективность открытий контролируется параметром открываемости  и фактором зрелости (изученности), т.е. размером выборки (доли - числа открытий относительно общего числа объектов). Поскольку геомаятниковый метод - непараметрический, вид родительского распределения (т.е. распределения в совокупности, взятой за основу при проведении экспериментов) мало влияет на результаты оценок. Для подтверждения и убедительности в процессе моделирования было использовано два вида распределения: логнормальное и Парето, и в каждом случае получены тождественные результаты оценок.

Остановимся на описании операции верификации метода. Варианты на моделях предоставляют такую возможность в наиболее доступном виде. Предполагается, что сымитированная последовательность “открытий” мало отличается от реальной, т.е. и первая, и вторая имеют вероятностную природу. Постулируется, что вероятность открытия напрямую зависит от размера “открываемого” объекта. Имитация “открытий” выполнялась как отбор объектов из генеральной совокупности без возвращения. Особая роль отводится параметру открываемости , изменяющемуся в диапазоне от 0,25 до 2,00. Применительно к случайной выборке из N как конечной совокупности используется термин родительская совокупность. Значения параметраравные 0,25; 0,5; 0,75; 1,0 и 2,0, определили число анализируемых сценариев.

Родительская совокупность “перемешивается” 1000 раз, что означает 1000-кратное случайное изменение порядка “открытия” объектов. Средние значения полученных величин, выстроенные в виде последовательности, в дискретном виде представят кривую математического ожидания случайной функции, которая в синтетическом виде отражает свойства, присущие генеральной совокупности, включая число входящих в нее объектов N и их суммарный объем R. Очевидно, что по мере увеличения размера последовательности, что достигалась в эксперименте ее постепенным расширением, можно ожидать (и в дальнейшем это экспериментально подтвердилось) существенного уменьшения стандартного отклонения вплоть до минимальных значений, что визуально может быть представлено как конус схождения 15-, 50- и 85%-х квантилей. Параметр  может быть известен априори или задан при предположении, что в родительской совокупности, по тем или иным причинам, в нарушение предполагаемого естественного состояния существует либо увеличение, либо уменьшение числа крупных объектов, и в этой связи имеется необходимость сгладить последовательность или, наоборот, сделать ее более контрастной.

Существует ли возможность оценить параметр  если его значение неизвестно до проведения операций по оценке R и N? Выполненные эксперименты (Forman D.J., Hinde A.L., 1985; Lee P.J., Wang P.C., 1985) показывают, что такие оценки возможны на моделях, когда представляется возможным использовать статистические характеристики мультивариационной регрессии, указывающие на связь между видом распределения сымитированной последовательности и оцениваемым параметром . Критерием эффективности таких оценок во всех случаях являлось сравнение вычисленных величин R и N c положенными в основу родительской совокупности. Очевидно, что на практике такую операцию можно выполнить на базе реальной выборки объектов, некоторой конечной совокупности из всех УВ-залежей в пределах нефтегазоносного бассейна.

Оценка ресурсов северных районовТимано-Печорской НГП с помощью геомаятникового метода

Тимано-Печорская провинция - это обширная территория, охватывающая в своей континентальной части площадь около 324 тыс. км2. Осадочный чехол, начинающийся с ордовикских отложений, имеет мощность от 3 до 7 км. На востоке, в Предуральском прогибе, мощность возрастает, достигая 10-12 км. В строении осадочного чехла отчетливо прослеживается горизонтальная локализованность в виде формационных рядов, представленных определенным набором формаций и образующих структурные ярусы, разделенные региональными перерывами. Выделяются 5 структурных ярусов: ордовик-нижнедевонский, среднедевон-триасовый, среднеюрско-нижнемеловой, верхнемеловой, четвертичный.

В состав провинции входят Печорский седиментационный бассейн и часть его структурного обрамления. В структурном плане Печорского седиментационного бассейна выделяется несколько крупных структурных единиц, в частности Нерицкая моноклиналь, Ижемская впадина, Омра-Лузская седловина, Малоземельско-Колгуевская моноклиналь, Печоро-Кожвинский мегавал, Денисовский прогиб, Колвинский мегавал, Хорейверская впадина, Варандей-Адьзвинская структурная зона. Отдельно в составе бассейна выделяются 4 впадины Предуральского краевого прогиба: Коротаихинская, Косью-Роговская, Большесынинская и Верхнепечорская.

Залежи нефти и газа обнаружены в отложениях палеозоя начиная с верхнего ордовика и кончая верхней пермью и в мезозое вплоть до среднего триаса. Частота встречаемости здесь зависит от ряда специфических факторов, которые специалисты использовали для районирования седиментационного бассейна по признаку нефтегенерации и ареалов нефтегазонакопления. В составе Тимано-Печорской провинции выделяется несколько нефтегазоносных областей, которые в свою очередь подразделяются на зоны, диазоны и, наконец, нефтегазоносные районы.

Известно, что любая математическая модель является абстрактным аналогом физической и есть ничто иное, как формализованное выражение некой реальной ситуации, характеризующейся единством формы и содержания. Применяя тот или иной способ математического моделирования, исследователь должен рассматривать объект как некоторую естественную общность, возникшую вследствие направленно действующих процессов и имеющую достаточно четкие границы.

Удобным объектом для проведения экспериментального счета представляется северо-восточная часть провинции (Садов С.Л., Тарбаев Б.И., Ушанов В.В. и др., 2000). Определяя эту территорию с точки зрения нефтегазонакопления как геологическое целое, подчеркнем, что субъекты нефтегазоносного районирования в его пределах имеют наибольшую плотность ресурсов на 1 км2 (Варандей-Адьзвинская нефтегазоносная область - 219,1 тыс. т усл. топлива/км2, Печоро-Колвинская нефтегазоносная область - 148,4 тыс. т усл. топлива/км2, Хорейверская нефтегазоносная область - 911,7 тыс. т усл. топлива/км2), что свидетельствует о благоприятных условиях генерации и накопления нефтегазоносных флюидов в его границах, способствующих превращению данного региона в своеобразный узел нефтегазонакопления.

В качестве первопричины, на которую наложились остальные благоприятствующие накоплению УВ процессы, специалисты рассматривают блоковые движения фундамента, обладающие различной тектонической активностью. Наивысшую активность имели блоки, выраженные в осадочном чехле в виде линейных, осложненных разрывами структур. Таковыми на рассматриваемой территории являются Денисовский, Колвинский и Варандей-Адьзвинский блоки, а занимающий между ними промежуточное положение Хорейверский блок как бы подчеркивает своеобразное структурное единство района, во многом предопределившее последующие сценарии геологического развития и режим нефтегазонакопления.

Исходными данными для выполнения процедуры оценки устойчивости и вычисления оценок прогнозных УВ-ресурсов служили запасы, выявленные в пределах рассматриваемой территории объектов в виде последовательности в порядке их открытия (Садов С.Л., Тарбаев Б.И., Вдовенко В.Л. и др., 2000).

При оценке устойчивости метода на базе конечной последовательности использован мультивариационный способ, обеспечивающий максимальную корректность полученных результатов. Величина параметра эффективности выявления месторождений b была приравнена к единице. Устойчивость метода оценивалась при помощи 15-, 50- и 85%-х квантилей от общего объема вариаций. Ширина коридора отклонений последовательно уменьшалась практически до 0 (рис. 1, 2, табл. 1). Результаты счета свидетельствуют об адекватности математических зависимостей реальной ситуации.

Чтобы вычислить прогнозные оценки УВ-ресурсов  и число возможных месторождений  в границах заданной площади геомаятниковым методом, необходимо оценить степень ее опоискованности или, если придерживаться зарубежной терминологии, состояние исследовательской зрелости. По смыслу это определение близко к понятию геологической изученности, хотя последняя отличается большой неопределенностью.

Нельзя не согласиться, что проведение границы между состоянием исследовательской зрелости и состоянием, ему предшествующим, не всегда гарантирует получение желаемого эффекта, поскольку не опирается на понятные и заслуживающие доверия критерии. Но в целом проведение такого рубежа для специалистов не составит особого труда, если они объективно взвесят всю совокупность геологических характеристик. На интуитивном уровне такой рубеж может означать состояние, когда пик открытий уже пройден и наблюдается очевидное снижение эффективности геологических исследований. Есть основание полагать, что север Тимано-Печорской провинции в границах, определенных выше, уже достиг исследовательской зрелости.

Вычисление объемов прогнозных ресурсов  и числа УВ-залежей  предполагает решение уравнения (7). Для этого достаточно воспользоваться, например, простыми методами последовательного приближения.

Оценка прогнозных геологических ресурсов УВ в границах рассматриваемой территории составила 8,9 усл. ед., число месторождений - 475 (рис. 3, табл. 2).

Выводы

Геомаятниковый метод - один из способов прогноза. По степени формализации все способы прогнозирования делятся на интуитивные и формализованные. Геомаятниковый метод относится к формализованным, для которых важным показателем является глубина прогноза. Они оказываются действенными, если глубина прогноза укладывается в некоторый интервал, определяющий эволюционный цикл и гарантирующий достоверность прогнозируемой величины. В методическом плане основным инструментом прогноза служит экстраполяция, которая бывает формальной и прогнозной. Формальная базируется на предположении о сохранении в будущем прошлых и настоящих тенденций. При прогнозной экстраполяции фактическое развитие увязывается с гипотезами о динамике исследуемого процесса с учетом его физической и логической сущности. Основу экстраполяционных методов составляют упорядоченные во времени или пространстве наборы измерений тех или иных характеристик. Временной ряд может быть представлен в виде

где- детерминированная неслучайная,- случайная компонента процесса.

Детерминированная компонентахарактеризует существующую тенденцию исследуемого ряда в целом, случайная компонентаотражает стохастические колебания. Естественно, что первым этапом экстраполяции является выбор оптимального вида функции, описывающей эмпирический ряд, и при необходимости преобразование исходных данных путем сглаживания и выравнивания временного ряда.

Зачастую наиболее эффективным и надежным способом прогнозирования является экспоненциальный метод, к достоинствам которого относится простота вычислительных операций, хотя, как и для всякого экстраполяционного метода, трудным моментом является выбор параметра сглаживания. Эта проблема решается тем или иным путем, но ни одна из сглаживающих операций не избавляет от неудобств. Метод экспоненциальной экстраполяции подробно описан в работах (Adelson R.M., 1966; Brown R.G., 1969; Легостаева И.Л., Ширяев А.Н., 1971; Клеопатров Д.И., Френкель А.А., 1973; Андерсон Т., 1976).

Известно, что при сходимости ряда применение экспоненциальной экстраполяции позволяет добиваться наивысшего эффекта. А для каждой нефтегазоносной провинции последовательность запасов открываемых месторождений - заведомо сходящийся ряд от самого крупного до мельчайшего (если угодно, до капли, которую можно приравнять нулю). Большинство формализованных алгоритмов, предназначенных для выполнения экстраполяции, предполагает упорядочение исходной выборки объектов по величине, справедливо предполагая, что экстраполяция по ряду, сходимость которого очевидна, будет заведомо эффективнее, чем по неупорядоченному. При этом, однако, игнорируется такое немаловажное обстоятельство как случайный характер величин открываемых месторождений. Сделанное замечание не находится в противоречии с устоявшимся вполне справедливым представлением о “геологическом фильтре”, согласно которому выявлению подлежат месторождения в порядке убывания от крупных к мелким. Не менее справедливо также утверждение, что поиск месторождений - процесс не случайный, поскольку ему предшествует изучение закономерностей размещения ловушек нефти и газа. Верно и первое, и второе, как верно и то, что размер ловушки не обязательно адекватен размеру приуроченной к ней залежи. К этому следует добавить, что порядок закладки скважин диктуется руководством геолого-разведочных компаний, которое не всегда следует предписанию “геологического фильтра”.

Из сказанного можно сделать вывод: случайная составляющая в последовательности выявленных месторождений - фактор, который нельзя игнорировать. Главное в таких ситуациях - обнаружить детерминированную компоненту, тенденцию, проявляющуюся на стадии исследовательской зрелости в неупорядоченной по размерам величин последовательности, имеющей свойство схождения. В процедуре геомаятникового метода эта проблема решается оригинально и эффективно.

Напомним еще раз, что изучаемые геологические объекты образуют конечную последовательность, и совокупность месторождений в пределах какой-либо нефтегазоносной территории не исключение. В известном смысле это сходящийся ряд, который замыкает некоторое месторождение. Его размер принимается в качестве минимального. Существующие экстраполяционные методы имеют свойственные им недостатки, к числу которых в первую очередь относится необходимость оценивать интервал экстраполяции, что заведомо связано с риском выйти за рамки, обеспечивающие приемлемый уровень прогноза. Геомаятниковый метод позволяет обойти эту трудность.

В самом общем виде заложенную в методе идею можно сформулировать так: открытие любого месторождения на совокупности всех объектов в границах нефтегазоносной территории имеет некоторую вероятность, а сумма вероятностей открытия всех месторождений равна единице. Поэтому, когда исследователь располагает конечной совокупностью выявленных объектов, которую он обозначает как , его задача сводится к вычислению “остатка” 1 - f. Таким образом, для исследователя нет необходимости задаваться глубиной интервала экстраполяции и прибегать к сглаживанию исходной последовательности, поскольку предел экстраполяции определен и в некотором смысле сведен к интерполяции, более устойчивой в прогнозном плане процедуре. Эксперименты, в процессе которых путем перестановок моделировались многочисленные комбинации, включая сглаженное среднее для всего ансамбля выборок, показали, что необходимость сглаживания отсутствует.

Поскольку речь идет о конечной выборке совокупности месторождений в пределах некоторой нефтегазоносной территории, сходящейся в случае ее упорядочения по крупности к какому-то пределу, то возникает вопрос - что считать этим пределом? В рамках геомаятникового метода ответ на этот вопрос дает сама выявленная последовательность, которую следует рассматривать как случайную выборку из генеральной совокупности. Сама такая постановка вопроса неправомерна. Понятие исследовательской зрелости в переводе на язык математической статистики означает представительность выборки, т.е. достижение такого уровня опоискованности, когда совокупность открытых объектов включает весь спектр месторождений по крупности, в том числе и такие, которые по размеру могут не представлять коммерческого интереса. Малые объекты могут быть пропущены по причине дефицита информации об их местонахождении. Но даже если ловушки тем или иным способом выявлены, зачастую они бывают не вскрыты бурением, как не представляющие до поры практической значимости. И то, и другое в принципе проявится как эффект усечения исходной последовательности и отразится на оценках объемов УВ-ресурсов  и числе месторождений

Надо полагать, именно этим обстоятельством объясняется расхождение оценок для северо-восточной части Тимано-Печорской провинции при использовании метода геомаятника (8,9 усл. ед., 475 месторождений) и алгоритма линейной аппроксимации распределения месторождений по крупности (12,2-17,0 усл. ед., 1460-1961 месторождение) [1].

Применение параметра эффективности открываемости месторождений b, как показали эксперименты, является нежелательной процедурой, поскольку ведет к явному искажению суммарного объема исходной последовательности и тем самым либо неоправданно завышает, либо занижает результаты оценок.

Геомаятниковый метод - это оригинальный и эффективный способ оценки УВ-ресурсов при условии достижения исследовательской зрелости, т.е. в случае, если исходная последовательность охватывает весь спектр месторождений, представляющий промышленный интерес. Однако и тогда, когда исследовательская зрелость по тем или иным причинам рассматривается в объеме заведомо усеченной выборки, метод успешно выполнит свое назначение.

Кроме того, можно сделать важный вывод, что применение геомаятникового метода для оценки УВ-ресурсов в пределах обширных территорий далеко не исчерпывает его возможности. Есть основания полагать, что его использование для оценки остаточных запасов на эксплуатируемых месторождениях, перешедших в стадию падающей добычи, позволит уточнить оставшиеся запасы нефти в провинции с достаточной степенью достоверности, причем оперативно и с малыми затратами.

Литература

1.     Шпильман В.И. Количественный прогноз нефтегазоносности. - М.:Недра, 1982.-216 с.

2.     Chen Z. Quantification of petroleum resources through sampling from a parent population and as a function of basin yield: doctoral thesis // The Norwegian Institute of Technology. - 1993. - 320 p.

3.     Chen Z., Sinding-Larsen R. Estimating petroleum resources using Geo-anchored method - a sensitivity study // Natural Resources Research. - 1999. - Vol. 8, N 1. - P. 49-58.

4.     Kaufman G.M. Finite population sampling methods for oil and gas resource estimation, in Rice D.D., ed., Oil and gas assessment - methods and applications: Am. Assoc // Petroleum Geologists Studies in Geology. - 1986. - N 21. - P. 43-54.

5.     Kaufman G.M. Successive sampling and software reliability // MIT Sloan School Working. - 1992, Paper 3316. - 34 p.

Abstract

The geoscillation method - the most advanced development in the sphere of hydrocarbon resources evaluation of oil- and gas-bearing provinces and their individual parts. Experimental testing of method’s convergence and estimation of the resources size and number of fields was carried out for the northern part of the Timano-Pechora oil- and gas-bearing province. Comparison with similar results obtained by other methods has demonstrated more conservative and realistic nature of estimates obtained by the geoscillation method.

 

Таблица 1 Сходимость результатов расчетов по проверке геомаятниковым методом

Расчетная база, число месторождений

Объем ресурсов, усл. ед.

Число месторождений

Нижняя граница

Среднее значение

Верхняя граница

Нижняя граница

Среднее значение

Верхняя граница

15

6,6305

6,8364

7,1091

57

87

145

20

6,6404

6,8243

7,0634

64

89

139

25

6,6530

6,8210

7,0326

71

91

135

30

6,6701

6,8151

7,0005

72

93

130

35

6,6852

6,8104

6,9527

76

94

129

40

6,6973

6,8012

6,9361

79

95

126

45

6,7079

6,7952

6,9092

81

95

122

50

6,7264

6,7935

6,8842

83

96

119

55

6,7334

6,7886

6,8571

85

97

116

60

6,7426

6,7888

6,8424

86

97

113

65

6,7489

6,7843

6,8304

88

98

111

70

6,7545

6,7810

6,8157

90

98

109

75

6,7595

6,7794

6,8083

91

98

107

80

6,7635

6,7784

6,7976

93

98

105

85

6,7689

6,7787

6,7916

94

98

103

90

6,7719

6,7774

6,7854

95

98

102

 

Таблица 2 Результаты прогнозных расчетов при расширяющейся базе прогноза

Прогнозная база, число месторождений

Объем ресурсов, уcл. ед.

Число месторождений

3

1,0463

13,0

8

8,5602

350,6

13

3,9368

92,7

18

17,9733

442,7

23

12,1839

242,4

28

10,8818

226,9

33

7,4266

138,8

38

5,2940

108,9

43

4,7114

53,6

48

6,6418

242,3

53

7,2253

267,7

58

9,9895

627,3

63

9,7626

572,0

68

8,6169

491,8

73

7,9892

398,2

78

7,8776

361,3

83

9,3055

541,9

88

9,4602

567,6

93

9,0392

512,5

98

8,9125

475,7

 

Рис. 1. СХОДИМОСТЬ ЗНАЧЕНИЙ ОБЪЕМОВ РЕСУРСОВ, ВЫЧИСЛЕННЫХ ПО ГЕОМАЯТНИКОВОМУ МЕТОДУ

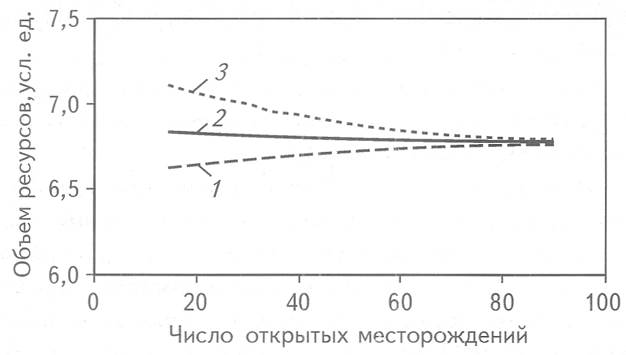
1 - нижняя граница; 2- среднее значение; 3-верхнее значение

 

Рис. 2. СХОДИМОСТЬ ЗНАЧЕНИЙ ЧИСЛА МЕСТОРОЖДЕНИЙ, ВЫЧИСЛЕННЫХ ПО ГЕОМАЯТНИКОВОМУ МЕТОДУ

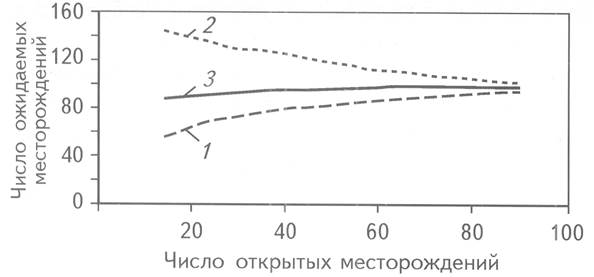
Границы оценки: 1 - нижняя, 2- верхняя, 3 – средняя

 

Рис. 3. РЕЗУЛЬТАТЫ ПРОГНОЗНЫХ РАСЧЕТОВ ГЕОМАЯТНИКОВЫМ МЕТОДОМ ПРИ РАЗЛИЧНОЙ ПРОГНОЗНОЙ БАЗЕ

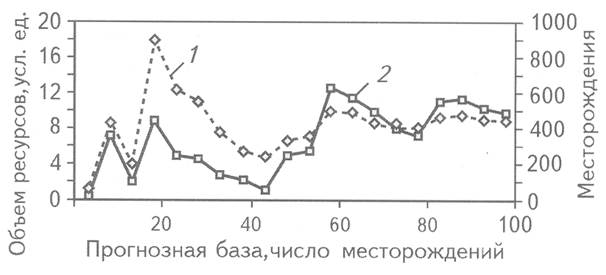
1 - объем ресурсов; 2 - число месторождений