|
© Коллектив авторов, 2005 |
ОПРЕДЕЛЕНИЕ ЗАПАСОВ ГАЗА В ПОДЗЕМНЫХ ХРАНИЛИЩАХ ГАЗА НА ОСНОВЕ ИСПОЛЬЗОВАНИЯ ХАРАКТЕРНЫХ ОСОБЕННОСТЕЙ ИХ ЦИКЛИЧЕСКОЙ ЭКСПЛУАТАЦИИ
В.В. Зиновьев, С.А. Варягов, В.Т. Боярчук, С.В. Беленко (ООО "Кавказтрансгаз")
Из известных двух методов подсчёта запасов газа для месторождений и подземных хранилищ газа (ПХГ) - объёмного и по падению (возрастанию) пластового давления, или материального баланса - более простым является второй. Однако методические основы этого метода предусматривают его использование для хорошо дренируемых залежей и ПХГ с газовым режимом.
Рассмотрим возможности использования указанного метода для ПХГ, эксплуатируемых при водонапорном режиме, а также для ПХГ, неоднородных по коллекторским свойствам с газовым режимом.
Особенностью эксплуатации ПХГ при водонапорном режиме является циклическое изменение газонасыщенного порового объёма продуктивной части пласта - уменьшение при отборе газа из ПХГ в результате внедрения пластовой воды, обусловленного снижением давления в пласте, и увеличение при закачке газа в ПХГ в результате оттеснения пластовой воды за пределы продуктивной части за счёт повышения давления.
В результате этого для ПХГ с водонапорным режимом, в отличие от упомянутых ПХГ с газовым режимом, графики зависимости приведённого средневзвешенного по поровому объёму пластового давления от текущих запасов газа - рт = f(Vт) имеют вид гистерезисной кривой (рис. 1).
При построении этих графиков одной из основных величин является приведённое средневзвешенное по газонасыщенному поровому объёму пластовое давление (далее - среднее пластовое давление).
При изменяющемся в процессе закачки и отбора газа газонасыщенном объёме, обусловленном перемещением газоводяного контакта (ГВК),
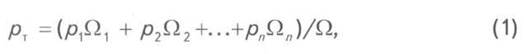
где р1, р2,..., рn -
определяемые по картам изобар пластовые давления в соответствующих
газонасыщенных поровых объемах
;
W - газонасыщенный поровый объем ПХГ на дату замера p1, р2, … ,рn.
где sB - коэффициент газонасыщенности.
Следовательно, в условиях перемещения ГВК при каждом
определении среднего пластового давления рт следует заново
определять все 
.
В практике же эксплуатации ПХГ при определении среднего пластового давления рт пользуются палеткой, построенной при последнем определении запасов газа в ПХГ объёмным методом, т.е. не учитываются изменения положения ГВК в процессе циклической эксплуатации.
Возникает вопрос: какова ошибка при определении рт
из-за неучёта этого фактора? Сразу ясно, что ошибки в определении рт
не будет в случае, если все 
изменятся
относительно начальных значений одинаковое число раз. Для правомерности
использования первоначальной палетки на Северо-Ставропольском ПХГ проведены
геофизические исследования, по результатам которых установлено, что
использование первоначальной палетки при определении рт при
изменениях 
, когда вариации общего
порового объёма W достигают
40 %, даёт ошибку, не превышающую 2 %, а когда изменение W не превышает 10 %, это практически не влияет на находимое
значение рт.
В процессе циклической эксплуатации при построении графиков рт = f(VT) расчётным значениям рт на оси абсцисс VT соответствуют объёмы газа, учитываемые по результатам закачки и отбора. Эти объёмы газа по известным причинам могут не соответствовать текущим запасам газа в ПХГ, но в пределах одного цикла эксплуатации ПХГ это несоответствие имеет некоторую постоянную величину (особенно при отборе газа).
Учитывая это, изложим методику определения запасов газа в ПХГ, эксплуатируемых при водонапорном режиме, с использованием характерных точек гистерезисной кривой рт = f(VT), в которых происходит смена знака процесса.
При этом предполагаем, что темпы отбора и закачки газа совпадают, и переход от закачки к отбору газа происходит без нейтрального периода. Из закона Бойля-Мариотта, записанного для текущего состояния ПХГ
следует
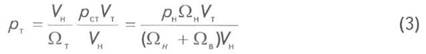
или в безразмерном виде
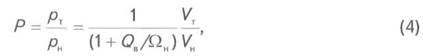
где рн и рт - начальное (равновесное) и текущее средние давления; VH и VT - начальные и текущие запасы газа в ПХГ; Wн и WТ - начальный и текущий объёмы порового пространства; Qв - объем воды, поступившей в поровое пространство ПХГ во время периода отбора (отрицательный) или оттеснённой из него в период закачки (положительный).
В точке А, которая является точкой возврата гистерезисной кривой, происходит смена процесса закачки газа на процесс отбора при продолжающем увеличиваться поровом объёме ПХГ. Естественно ожидать, что эти процессы должны отражаться на поведении гистерезисной кривой в окрестности точки А (см. рис. 1).
Определим угловые коэффициенты односторонних касательных к кривым закачки и отбора газа в точке А. Для этого используем формулу (4). В этой формуле неизвестен вид функции Qв = f(Vт). Однако из практики эксплуатации ПХГ известно, что в последние дни периода закачки функция Qв = f(VT) монотонно возрастает и продолжает ещё возрастать некоторое время, несмотря на начавшийся отбор газа из ПХГ и уменьшение текущих запасов Vт, поскольку текущее давление рт ещё выше давления на внешнем контуре водоносной системы. То есть в окрестности точки возврата А, несмотря на начавшееся в период отбора уменьшение VT, функция Qв = f(VT) ведёт себя так, как если бы текущие запасы VT все ещё продолжали возрастать. Этим объясняется то, что линия отбора газа AD лежит ниже прямой OA, которая характеризовала бы работу ПДХ, если бы режим его работы, начиная с точки А, вдруг стал газовым.
Полагая, что Qв = f(VT) дифференцируемая функция для значений VT, близких к Vта, можно записать:
Откуда 
Или 
Где 
С учётом (5) представим (4) в окрестности точки А в виде
Где 
Найдём односторонние производные 
для конца закачки и начала отбора,
т.е. при Vт = VTa, а затем среднее значение угловых касательных
коэффициентов. Учитывая характер изменения Qв в зависимости от VT
при изменении знака приращения VT,
запишем (6) в следующем виде:
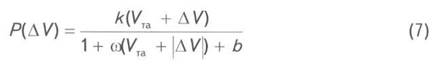
и найдём односторонние производные в точке DV=0 (VT=VTa), используя определение производной. Отношение приращений
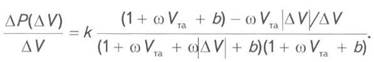
Отсюда для закачки, учитывая, что
при
DV>0, находим
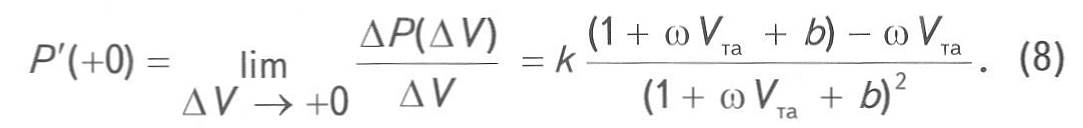
Для отбора 
при
DV<0
и
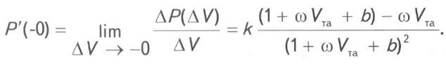
Средняя величина равна
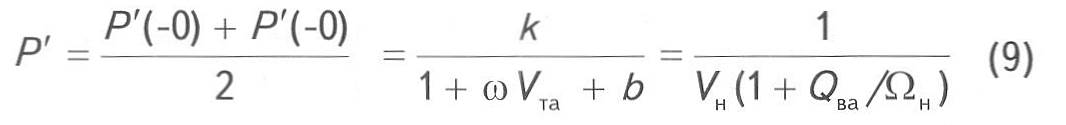
или в размерном виде
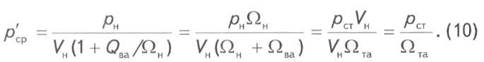
Легко видеть, что выражение (10) совпадает с угловым коэффициентом прямой OA, исходящей из начала координат. Действительно, из формулы (2) и рис. 1 следует, что угловой коэффициент равен
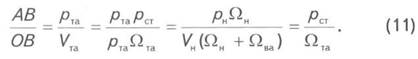
Аналогичные рассуждения справедливы и для перехода от отбора к закачке газа (прямая OF). Поэтому все прямые со средними угловыми коэффициентами должны исходить из одной точки на оси запасов.
Следовательно, имея фактические данные о гистерезисном поведении кривой рт = f(Vт), можно, проведя прямую с угловым коэффициентом, средним из угловых коэффициентов односторонних касательных, до пересечения с осью запасов, установить фактическое положение начала координат и тем самым определить текущие запасы газа в ПХГ. Допущение о постоянстве скорости изменения текущего порового объёма при переходе от закачки к отбору и, наоборот, при отсутствии нейтрального периода является существенным. И чем меньше окрестность VТА, в которой это допущение выполняется, тем труднее правильно провести односторонние касательные.
В последнее время большое внимание стало уделяться аспектам техногенного воздействия циклической эксплуатации на коллектор ПХГ. Доказывается, что такая эксплуатация может привести к появлению зон, значительно различающихся по коллекторским свойствам [1]. Поэтому следует ожидать, что гистерезисные кривые рт = f(VT) могут получаться и при эксплуатации ПХГ при газовом режиме, если имеется газодинамическая связь между пластами с разными коллекторскими свойствами или разделёнными слабопроницаемой перемычкой. Гистерезис будет обусловлен запаздыванием изменения давления при перетоках между ними (Зиновьев И.В., Беленко С.В., Боярчук В.Т. и др., 2001). Пусть, например, 1-й менее проницаемый или отделённый слабопроницаемой перемычкой пласт будет нижним, а 2-й более проницаемый пласт - верхним, и ПХГ эксплуатируется сеткой скважин, пробуренных только на верхний пласт. Тогда уравнения материального баланса для 1-го и 2-го пластов следующие [2]:
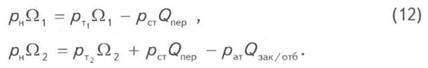
Решив второе уравнение относительно
, получим
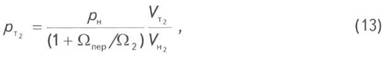
Где 
- текущие средние приведённые
давления в 1-м и 2-м пластах соответственно; W1, W2- поровые объёмы 1-го и 2-го пластов соответственно; Qзак/отб - накопленный объем
закачанного в период закачки газа (считается положительным) и объем добытого
газа в период отбора (считается отрицательным);
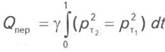- накопленный объем газа, перетёкшего из одного пласта в другой;
- коэффициент, определяющий
интенсивность перетока газа;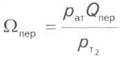
имеет
смысл как бы приращения порового объёма 2-го пласта на объем перетёкшего в 1-й
пласт газа, приведённого к
, которое
устанавливается во 2-м пласте при поступлении в него Qзак/отб
за вычетом Qпер.
Таким образом, все изложенное о нахождении QT остаётся в силе, но Wт приобретает смысл WT =W2 + Wnep.
Из изложенного следует, что получение гистерезисного графика pТ=f(VT) при циклической эксплуатации ПХГ ещё не даёт возможности утверждать, что оно эксплуатируется при водонапорном режиме и, чтобы получить представление о том, какая причина обусловливает гистерезисность графика, следует иметь сведения о перемещении ГВК (изменении газонасыщенной толщины пласта). Они позволяют судить об особенностях проявления водонапорного режима. На рис. 2 показан график изменения газонасыщенной толщины пласта в скв. 82н Северо-Ставропольского ПХГ в зависимости от пластового давления в месте ее расположения в цикле эксплуатации 1999-2000 гг. Здесь видно, что газонасыщенная толщина пропорциональна пластовому давлению. При этом не наблюдается запаздывания увеличения газонасыщенной толщины в начале периода закачки и запаздывания уменьшения - в начале периода отбора, как это следовало бы из теории эксплуатации ПХГ при водонапорном режиме. Такие же графики были получены ещё в пяти скважинах, находящихся на периферии ПХГ. Такая прямая зависимость газонасыщенной толщины от пластового давления наводит на мысль о подобной зависимости изменения порового объёма от изменения среднего пластового давления, т.е.:
где рн - начальное среднее (равновесное) пластовое
давление;
- коэффициент
пропорциональности.
Из (14) и уравнения материального баланса
Для определения Рт получаем квадратное уравнение
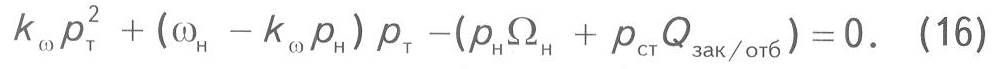
С использованием (16) сделан примерный расчёт рТ =
f(VT) для Qн = 100 млн.м3;
рн = 7 МПа; VH =
7 млрд.м3; QcyT =
±25
млн. м3/сут; число суток симметричного цикла закачки и
отбора 180; 1 -
=0; 2 -
=5,0; 3 -
=
50 млн.м3/МПа (рис. 3).
В силу (14) графики рт = f(Vт)
представляют собой одни и те же линии при отборе и закачке,
которые, несмотря на нелинейность рт = f(VT),
очень близки к прямым линиям, что может привести к ошибочным
заключениям о режиме эксплуатации как о газовом и соответственно об увеличенных
запасах газа.
Выражение для уклона касательной к линии в точке (Vн, рн) выглядит как
Значение 
можно
оценить по промысловым данным и, используя (17), найти Wн
и затем уточнить запасы VH.
Если изменение газонасыщенного порового пространства,
описываемое формулой (14), сочетается ещё и с перетоками газа между отдельными
зонами ПХГ, обусловленными различием коллекторских свойств последних, то
увеличение 
будет оказывать скрадывающее
действие на гистерезис зависимости рт = f(VT),
уменьшая разность давления между зонами. Это следует из того,
что вместо формулы (13) будем иметь:
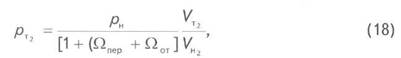
где
На рис. 4 показаны
графики таких зависимостей, построенные по следующим исходным данным: WH= 100 млн м3; объёмы верхнего и нижнего пластов
соотносятся как 1/2; рн= 7 МПа, Qсут=
±16,6 млн.м3/сут; число суток периодов закачки и отбора -
180; графики 1-
= 10-4 млрд м3/МПа и 2 -
= 10-2
млрд м3/МПа; интенсивность перетока газа между зонами с разными
коллекторскими свойствами взята пропорциональной разности квадратов средних
давлений: 
где g = 10-5
млрд м3/МПа.
Видно, что при малых значениях 
работает
только один (верхний) пласт, а при больших значениях 
график выполаживается.
Для определения запасов газа можно использовать и другие характерные точки гистерезисного графика. Такими точками являются точки, соответствующие прекращению перемещения ГВК (E и D на рис. 1). Они не обязательно должны соответствовать равновесному давлению [3]. Касательные к гистерезисному графику в этих точках могут указать правильное положение начала координат на оси запасов газа в ПХГ. Положение самих точек на гистерезисном графике может быть уточнено по данным о слежении за ГВК геофизическими методами.
Литература
1. Гридин В.А. Модель формирования коллектора / В.А. Гридин, С.А. Варягов, В.Г. Вершовский и др. // Газовая промышленность. - 2001. - № 1.
2. Закиров С.Н. Проектирование и разработка газовых месторождений / С.Н. Закиров, Б.Б. Лапук. - М.: Недра, 1974.
3. Левыкин Е.В. Технологическое проектирование хранения газа в водоносных пластах. - М.: Недра, 1973.
There are available two methods of gas reserves evaluation for fields and underground storages - volumetric and by decrease (increase) of formation pressure or physical balance. The second one appears to be more simple, however the methodical bases of this method envisage its using for well drained pools and storages with gas regime. The authors consider possibilities of using volumetric method for underground storages being exploited under hydrostatic regime as well as for storages being heterogeneous by reservoir properties with gas regime. In process of underground gas storages exploitation it is necessary to know its remaining volumes, therefore the authors suggest for solving this task to use graphs of relationship between average formation pressure and current gas reserves considering gas-water contact displacement under cyclic exploitation of storages.
Рис. 1. ГИСТЕРЕЗИСНАЯ КРИВАЯ ПХГ
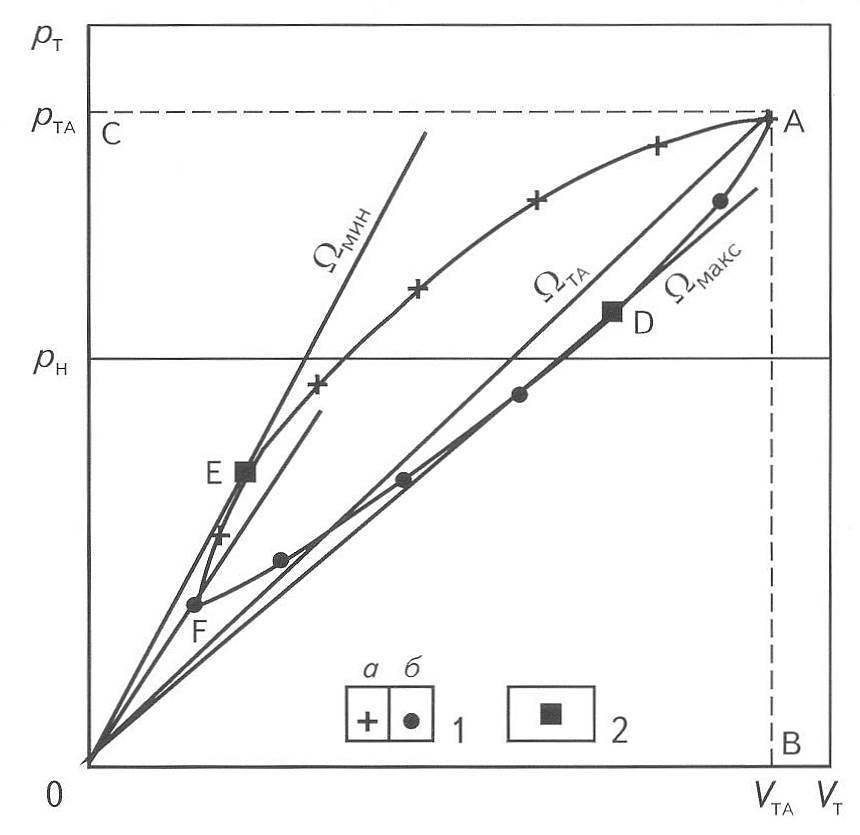
1 - точки, изображающие значения среднего пластового давления в период закачки (а) и отбора (б); 2-точки касания; W мин, W макс - соответственно минимальный и максимальный поровые объёмы ПХГ, достигаемые в цикле эксплуатации
Рис. 2. ЗАВИСИМОСТЬ ГАЗОНАСЫЩЕННОЙ ТОЛЩИНЫ ПЛАСТА В СКВ. 82Н СЕВЕРО-СТАВРОПОЛЬСКОГО ПХГ ОТ ПЛАСТОВОГО ДАВЛЕНИЯ В ЦИКЛЕ ЭКСПЛУАТАЦИИ 1999-2000 гг.
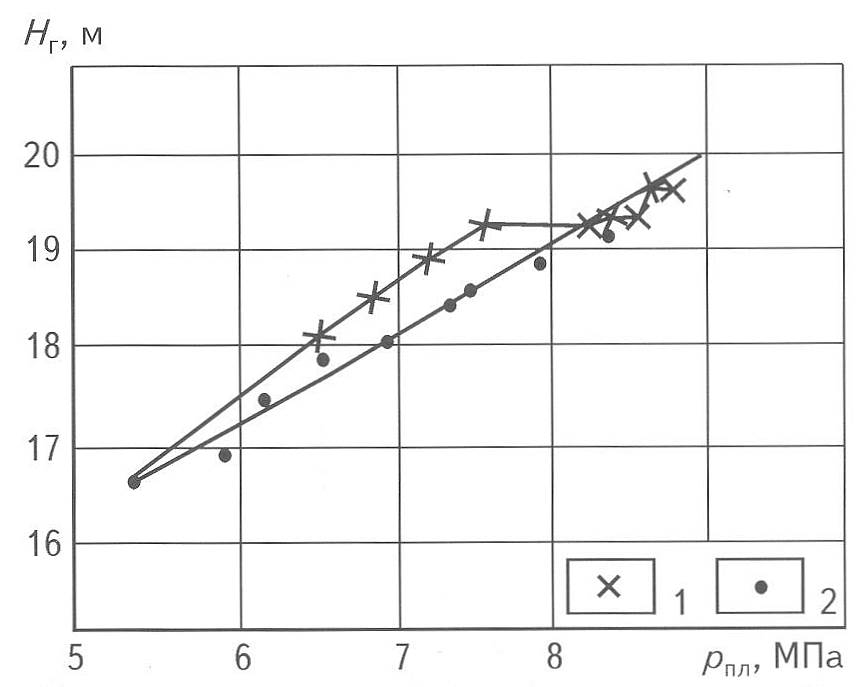
1 - закачка; 2 - отбор
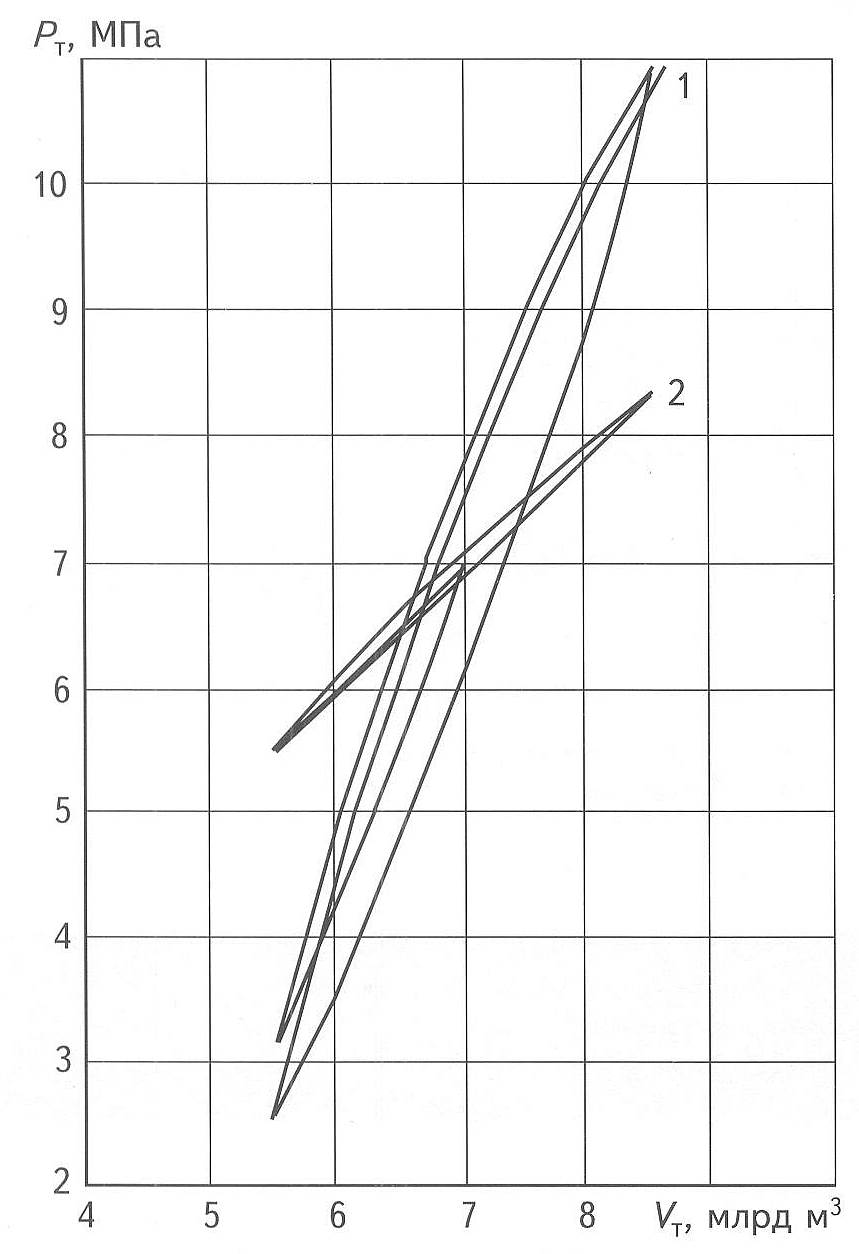
Рис. 3. ГРАФИКИ ТЕКУЩЕГО СРЕДНЕГО
ПЛАСТОВОГО ДАВЛЕНИЯ В ЗАВИСИМОСТИ ОТ ЗАПАСОВ ГАЗА В ПХГ ПРИ РАЗЛИЧНЫХ ЗНАЧЕНИЯХ
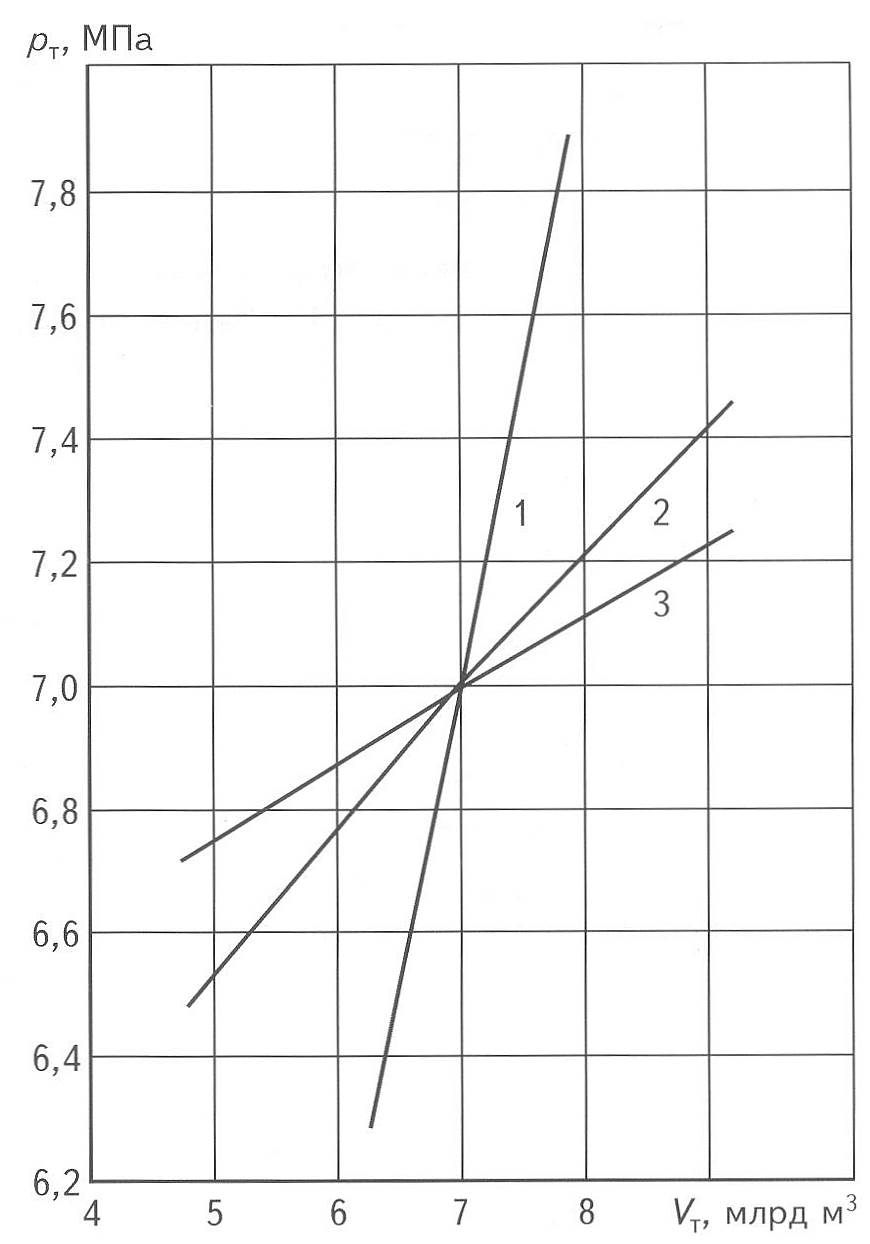
Рис. 4. ГРАФИКИ ТЕКУЩЕГО СРЕДНЕГО
ПЛАСТОВОГО ДАВЛЕНИЯ В ЗАВИСИМОСТИ ОТ ЗАПАСОВ ГАЗА В ПХГ при g =
10-5 млрд м3/МПа И РАЗЛИЧНЫХ
ЗНАЧЕНИЯХ 
