К оглавлению

© Р.Б. Булгаков, О.Р. Привалова, 2006

АНАЛИЗ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ПЕТРОФИЗИЧЕСКИХ СВЯЗЕЙ

Р.Б. Булгаков (ОАО "Башнефтегеофизика"), О.Р. Привалова (ДООО "Геопроект")

Проблемы петрофизического обеспечения интерпретации ГИС и подсчета запасов до сих пор остаются актуальными. Достоверность, качество и особенности использования данных по керну в геофизике включают ряд важнейших вопросов, в различной мере решаемых или пока нерешенных в практике работ (Булгаков Р.Б., 2000; Булгаков Р.Б., Ишбулатова Р.Х., Привалова О.Р., 2002; [1]).

Отбор и вынос керна многие 10-летия были важной проблемой в отечественном бурении на нефть и газ, однако в последние годы имеются многочисленные примеры планомерного производственного отбора керна в больших количествах при его выносе 85-100 %.

Привязку керна к глубине, несмотря на любые методические ухищрения, при низком проценте выноса керна надежно сделать невозможно. Задача решается только при полном (не менее 80-90 %) выносе керна.

Выбор образцов керна и составление коллекции только на первый взгляд кажутся простыми задачами. Важно не только (и не столько) получить полную, "представительную", с "нормальным распределением" коллекторских параметров коллекцию, но и тесно увязать параметры керна с ГИС, а для этого необходимо выбирать образцы равномерно по интервалу исследования, не выбрасывая, как это часто делается, пропластки с ухудшенными параметрами или неколлекторы.

Подготовка образцов к лабораторным анализам, на наш взгляд, один из наименее разработанных вопросов петрофизического обеспечения в нефтепромысловом деле. До настоящего времени не обоснована необходимость к началу лабораторных анализов отмыть керн в сильных растворителях, экстрагировать из него все УВ, битумы, органику, высушить при высокой температуре и тем самым привести его в такое состояние, в котором данная порода никогда не была и не будет. По таким образцам некорректно определять пористость, проницаемость, электрические параметры, остаточное водонасыщение. Только с введением специальной технологии можно будет определиться в вопросе подготовки образцов к различным анализам.

До сих пор не доработаны до уровня общепринятых методик вопросы изучения образцов в пластовых термобарических условиях - когда они необходимы, а когда можно обойтись исследованиями в лабораторных условиях или пересчетом, какова мера внесенных недоучетом пластовых условий ошибок.

Точность собственно лабораторных методов определения петрофизических параметров нельзя оценить однозначно. Казалось бы, при современном развитии лабораторной техники доступно определение большинства параметров с любой наперед заданной точностью. На практике же это далеко не так. Сходимость повторных измерений, воспроизводимость определений, выполненных на одной и той же коллекции образцов в различных лабораториях, свидетельствуют об ошибках измерений в пределах 10-20 % (иногда и более). Это вызвано огрехами при исполнении лабораторных работ (например, недонасыщение образцов жидкостью ведет к ошибкам в определении пористости, а это, в свою очередь, параметров Р_П(К_П), K_п (Dt) и др.) либо недостаточной разработанностью теории и методики анализа, например остаточного водонасыщения и связанных с ним параметров.

Необходимость комплексного изучения петрофизических параметров керна никто не отрицает, но на практике исследование керна растягивается: сначала первоочередные, важные анализы, затем они наращиваются по мере поступления заказов от тех или иных заинтересованных служб и по мере обеспечения оплаты. Но комплексность необходима не сама по себе, не только для полноты изучения коллектора, а как единый процесс на одних и тех же образцах керна для достижения большей тесноты корреляционных связей параметров керн - керн, т.е. большей достоверности петрофизической модели коллекторов. Кроме того, сейчас при высоком проценте выноса керна стала очевидной значительная неоднородность физических свойств коллекторов, не улавливаемая даже самыми детальными методиками ГИС. В этих условиях только частая и равномерная выборка образцов и их комплексный анализ могут помочь правильно сгруппировать данные керна и сопоставить их с показаниями методов ГИС. С учетом упомянутой важности подготовки образцов к анализам, причем неодинаковой для различных видов анализов, приходится говорить о необходимости определенной технологической цепочки анализа керна для нужд геофизики, подсчета запасов и разработки. Она должна включать следующее.

Если керн отобран при бурении на нефильтрующихся промывочных жидкостях (на нефтяной основе, известково-битумных, аэрированных и др.), т.е. с сохранением пластовых характеристик насыщения, прежде всего, должны быть определены естественные или близкие к естественным значения нефте- и/или водонасыщения и остаточного нефте- и водонасыщения.

Первоначально следует отмывать образцы только от подвижных пластовых флюидов с минимальным воздействием на смачиваемость стенок пор и без удаления твердых и вязких неподвижных УВ. На этих образцах определяются фильтрационно-емкостные свойства и другие важнейшие параметры (К_п, Кпр, К_в, Р_н, Рп, К_во, объемные и минеральные плотности, акустические скорости, диффузионно-адсорбционные потенциалы, гамма-активность).

На следующем этапе можно проводить экстракцию всех битумоидов, растительных остатков, кокса, угля, если ставится задача изучения их состава и количества.

На последнем этапе проводятся анализы, требующие разрушения образцов: гранулометрия, глинистость, карбонатность, водородосодержание глин, включая поровую и кристаллизационную воду.

Наконец, последней задачей петрофизического обеспечения интерпретации ГИС является построение петрофизических связей на основе результатов исследования керна, оценка их тесноты, достоверности, отыскание их аналитического представления и оценка точности определения искомых параметров с использованием этих петрофизических связей. Принято считать, что в этой области особых трудностей нет - керн поднят, исследован, увязан по глубине с ГИС, исследователь вооружён теорией статистики и вычислительными средствами. Между тем проведённый нами анализ петрофизических связей, полученных различными организациями за 10-летия разведки и разработки месторождений Башкортостана, позволяет выделить ряд уязвимых мест при получении и использовании этих связей для интерпретации данных ГИС.

При анализе нескольких сот петрофизических связей К_П(DI_ГК), К_пр(К_п), P_п(Кп), Р_Н(К_В), Кво(Кп) определялись:

обычный для таких случаев коэффициент корреляции r (или корреляционное отношение  для криволинейных зависимостей);

редко используемый показатель существенности коэффициента корреляции в виде:

отношений r или к погрешности их определения

где(при n > 100),

или неравенства

где t_st - критерий Стьюдента, определяемый по специальным таблицам с учетом заданного уровня значимости (обычно 0,01-0,05 при n < 100);

показатель разброса фактических точек, а именно среднеквадратическая величина отклонения точек от линии регрессии

т.е. ширина коридора вдоль линии регрессии, в который попадают 68 % точек, использованных для построения данной петрофизической связи.

Анализ показал, что первые два критерия слишком "либеральные": в сотнях рассмотренных примеров, за исключением 2-3 случаев, несмотря на небольшое обычно число точек и их значительный разброс, значение  составляет 0,80-0,98, редко снижается до 0,60, а проверка существенности связи дает положительный результат, часто превышающий необходимый минимум в десятки раз. Эти критерии свидетельствуют о существовании и тесноте статистической связи между петрофизическими параметрами. Но только показатель  позволяет оценить практическую пригодность полученной связи, так как он свидетельствует о ширине доверительного интервала, определяющей значение погрешности единичной оценки искомого параметра при использовании данной связи.

При оценке коэффициента корреляции на практике ему придается гипертрофированная роль. Между тем недостатком этих критериев является не только их "либеральность", но и широко распространившиеся приемы искусственного улучшения во вред истине.

Первым таким недопустимым приемом служит оценка тесноты петрофизических связей на основе групповых данных эксперимента. Например, зависимость, полученная на основе ста пар измерений параметров х и у, характеризуется коэффициентом корреляции r = 0,82, уравнение регрессии имеет вид у = 0,53х + 19 (рис. 1, А). Но если разбить все результаты наблюдений на десять групп, а точки в каждой группе заменить одной со средними значениямии, то сопоставление образовавшихся новых десяти групповых точек характеризуется следующими показателями:  уравнение регрессии у = 0,53х +18,91 (см. рис. 1, Б).

Утрируя для наглядности решение задачи, можно довести число групповых точек до двух, разделив исходный массив на две равные части, при этом  у= 0,50х+ 20,31. Полученные результаты, особенно последний, показывают, что данный путь, несомненно, ведет к абсурду (см. рис. 1, В).

Рассмотрим другой случай искусственного повышения коэффициента корреляции на примере акустических исследований керна. Сопоставление коэффициента пористости К_п и интервального времени Dt (рис. 2, линия 1) в диапазоне реальных коллекторов характеризуется значительным разбросом точек с коэффициентом корреляции r = 0,65, но стоит ввести всего одну новую, казалось бы вполне правомерную, точку "воды" (Кп = 100 %; Dt = 620 мкс/м), коэффициент корреляции увеличивается до 0,97 (см. рис. 2, линия 2). Аналогично улучшается коэффициент корреляции введением точки "воды" (Кв = 1; Р_н = 1) в зависимость Р_Н(Кв). Однако в подобных случаях такое не обосновано. Об этом свидетельствует значение , которое мало изменяется от прибавления такой точки и, таким образом, сохраняет свою роль как критерий пригодности связи для количественных оценок.

Напомним, что коэффициент корреляции зависит от расположения точек, т.е. наблюдаемых пар значений сопоставляемых параметров, но не зависит от расположения линии регрессии и вообще от ее существования или отсутствия. Отыскание линии регрессии методом наименьших квадратов, получившим широкое распространение, далеко не всегда правомерно. Оно правомерно при сопоставлении двух параметров, один из которых по отношению к другому является принципиально более точным, эталонным, и разброс точек вызван погрешностями только в значениях одного из них. Таким сопоставлением является, например, градуировка некоего упрощенного, рядового, рабочего измерителя (вольтметра, оптического дальномера, манометра и др.) с помощью высокоточного эталонного прибора. Любые сопоставления (может быть, за редким исключением) будь то керн - керн, керн - ГИС или ГИС - ГИС содержат значения параметров, измеренные с погрешностями одного порядка, т.е. являются в отношении уровня ошибок измерения равносторонними, симметричными [1]. В этих случаях нельзя сводить отыскание линии регрессии у(х) лишь к формальному применению метода наименьших квадратов.

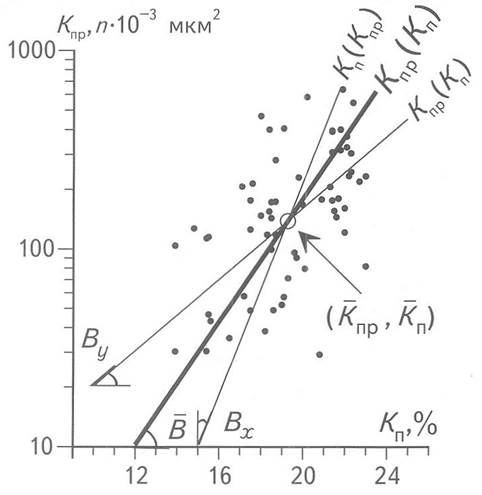
Дело в том, что линии регрессии у(х) и х(у), полученные методом наименьших квадратов, не совпадают и тем больше расходятся, чем ниже значение r. "Статистики-теоретики” считают эту двойственность неизбежной, лежащей в основе корреляционного анализа. Статистики-практики не могут примириться с этим. Они предложили несколько методов получения единого, или срединного уравнения регрессии" [3], однако ни один из них этим автором не приводится. Способ расчета этим автором "единой обобщенной регрессии", предложенный в [1], непригоден для практического применения ввиду нечеткости описания, неисправленных опечаток и отсутствия точной ссылки на первоисточник. Нами применяется следующий несложный метод (рис. 3). Рассмотрим его на примере отыскания линейной связи К_пр(Кп), для наглядности взяв случай нетесной связи (r = 0,62).

Из [2] известны следующие отношения:

где- угловые коэффициенты линии регрессии у(х), х(у) и средней искомой линии регрессии, которая отражает связь между у и х как равными в отношении ошибок измерения параметрами, т.е. делает ее симметричной. Все три линии пересекаются в одной точке с координатамии, т.е. в центре тяжести массива экспериментальных точек.

Для проведения симметричной линии регрессии практически нет необходимости отыскивать обе регрессии у(х) и х(у). Достаточно методом наименьших квадратов найти регрессию у(х) и изменить наклон ее линии по формуле

полученной в результате элементарных преобразований приведенных отношений.

Выводы

1. Коэффициент корреляции r является необходимой, но недостаточной характеристикой пригодности петрофизической связи для количественных определений.

2. Расширение области сопоставления параметров добавлением одиночных точек, хоть бы и правомерных, но выходящих за пределы рабочего диапазона, лишь искусственно повышает значение r, но не улучшает доверительный интервал такой зависимости.

3. Замена исходных пар единичных измерений петрофизических параметров осредненными (групповыми) точками при построении линии связи принципиально недопустима, так как ведет к ложному благополучию не только коэффициента корреляции, но и (что важнее!) оценки s, единственного для исследователя мерила возможных погрешностей при количественной оценке параметров с применением данной связи.

4. При значении коэффициента корреляции связи линию и уравнение связи, полученные методом наименьших квадратов, необходимо приводить к симметрированному виду по изложенному способу.

Литература

1. Орлов Л.И. Петрофизические исследования коллекторов нефти и газа / Л.И. Орлов, Е.Н. Карпов, В.Г. Топорков. - М.: Недра, 1987.

2. Тенант-Смит Дж. Бейсик для статистиков. Перевод с англ. - М.: Мир, 1988.

3. Шарапов И.П. Применение математической статистики в геологии. - М.: Недра, 1971.

Abstract

Petrophysical provision of well-logging data interpretation is of current interest problem especially in evaluating hydrocarbon raw material reserves. Reliability of estimation and other parameters which are determined by well-logging data to a great extent depends on petrophysical model reliability.

The authors consider most "close" and extremely important aspects of petrophysical provision in oil-field activity: collection of samples and their preparing for laboratory analysis, technological chain of core analysis for geophysical purposes, reserves estimation and development, different means of petrophysical relations construction, evaluation of practical adaptability of relations obtained. Scientifically based recommendations on constructing regression lines and petrophysical relations equations are given.

Of important task is petrophysical relations construction based on core studies results, assessment of reliability, their closeness, etc. From several hundreds of petrophysical relations analysis the following conclusions were drawn.

Correlation factor r is important but not sufficient characteristic of petrophysical relation suitability for quantitative definitions.

Widening the scope of parameters correlation by adding single points which are even though correct but being beyond the working range limits, only artificially increases a value r and however does not improve a reliable interval of such dependency.

Substitution of initial pair of single measurements of petrophysical parameters by averaged ("group") points in constructing relation line is principally inadmissible since causes the false satisfaction not only by correlation factor but - what is critical - in estimating , the only standard of possible errors in quantitative evaluation of parameters when applying this relation.

When a value of relation correlation factor |r| < 0,95-0,97, it is necessary to adjust the line and equation of relation obtained by the least squares method to symmetric form.

Рис. 1. ИСКУССТВЕННОЕ УЛУЧШЕНИЕ ПОКАЗАТЕЛЕЙ ТЕСНОТЫ СВЯЗИ ЗА СЧЕТ ОСРЕДНЕНИЯ ГРУППОВЫХ ДАННЫХ

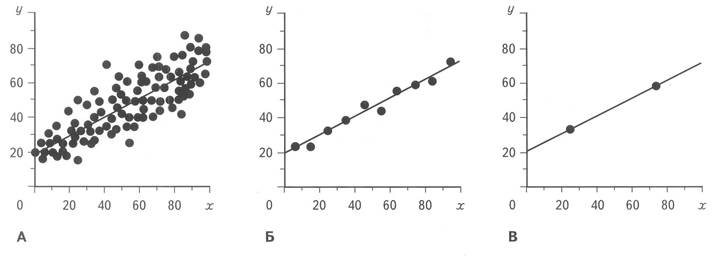
Рис. 2. ИСКУССТВЕННОЕ УЛУЧШЕНИЕ ПОКАЗАТЕЛЕЙ ТЕСНОТЫ СВЯЗИ ЗА СЧЕТ "ТВЕРДОЙ ТОЧКИ"

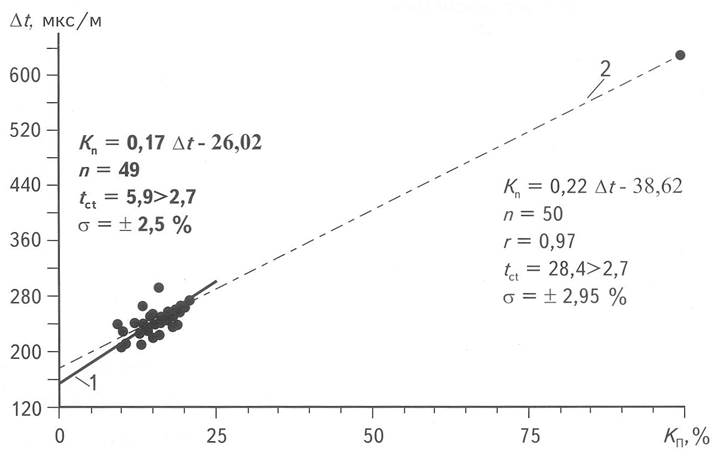
Рис. 3. ПОСТРОЕНИЕ СИММЕТРИРОВАННОЙ ЛИНИИ РЕГРЕССИИ