К оглавлению

© Б.И. Тарбаев, С.Л. Садов, 2006

УЧЕТ НЕОПРЕДЕЛЕННОСТИ ЧИСЛЕННЫХ ХАРАКТЕРИСТИК ПРИ ЭКОНОМИЧЕСКОЙ ОЦЕНКЕ ПЕРСПЕКТИВНЫХ РЕСУРСОВ УГЛЕВОДОРОДОВ

Б.И. Тарбаев, С.Л. Садов (Институт социально-экономических и энергетических проблем Севера КНЦ УрО РАН)

По действующей временной классификации ресурсы нефти и газа, относящиеся к категории С₃, определяются как “...перспективные ресурсы нефти и газа подготовленных для глубокого бурения площадей, находящихся в пределах нефтегазоносного района и оконтуренных проверенными для данного района методами геологических и геофизических исследований, а также не вскрытых бурением пластов разведанных месторождений, если продуктивность их установлена на других месторождениях района”. Обычно в таких случаях речь идет о предполагаемых залежах на выявленных теми или иными методами геологических объектах. Это означает, что оценки величин приписываемых объекту объемов УВ лежат в некотором диапазоне, не исключая околонулевых значений, при которых освоение ресурсов заведомо убыточно. Очевидно, что стоящая перед потенциальным инвестором задача оценки эффективности вложений в доразведку и освоение перспективных ресурсов УВ решается в условиях неопределенности, причем решение будет зависеть от учета определяющих ее факторов. Отметим, что данная задача значима ввиду опасности ориентации развития нефте- и газодобычи в долгосрочной перспективе на слабо обоснованные показатели объемов ресурсов категорий низкой разведанности. Влияние факторов неопределенности на рентабельность запасов и ресурсов УВ признается в новой Классификации запасов и ресурсов нефти и горючих газов, утвержденной приказом Минприроды РФ 1 ноября 2005 г., в которой впервые введены экономические показатели в целях оценки УВ, соответствующие рыночным отношениям в недропользовании. Традиционный же подсчет перспективных ресурсов, игнорирующий вероятностный подход и связанную с ним неопределенность, осуществлялся в течение многих 10-летий с результатами, нашедшими отражение во многих официальных документах. Естественно, необходимые в таких случаях оценки рассеивания показателей ресурсов, приуроченных к геологическим объектам, в частности рекомендованные в [1], не выполнялись. Предлагаемый авторами статьи метод позволяет решать задачу определения диапазона объемов ресурсов по приписанному им значению с учетом новых подходов, выстраивая оптимальную стратегию инвестирования в освоение ресурсов нефти и газа, важную не только в масштабах отрасли, но в конечном счете для экономики страны в целом.

Для решения такой задачи воспользуемся математическим аппаратом теории нечетких множеств, широкое прикладное значение которой предсказал еще в 1965 г. ее основатель Л. Заде: “Фактически нечеткость может быть ключом к пониманию способности человека справляться с задачами, которые слишком сложны для решения на ЭВМ” [2]. Предупреждая возможный вопрос: почему бы при оценке вероятности присутствия на объекте залежи с локализованными перспективными ресурсами С₃ не воспользоваться статистическими приемами? - обратим внимание на специфику выборки при проведении соответствующих работ. В самом простом виде вероятность открытия залежи в контурах некоторого геологического объекта будет определяться как отношение успешных результатов к общему числу обследованных объектов. Однако такой результат может иметь смысл и использоваться для прогноза лишь при условии однородности выборки (обследованных объектов), которое в подавляющем большинстве случаев не соблюдается из-за геологических особенностей каждого объекта, его уникальности несмотря на некоторые черты внешнего сходства.

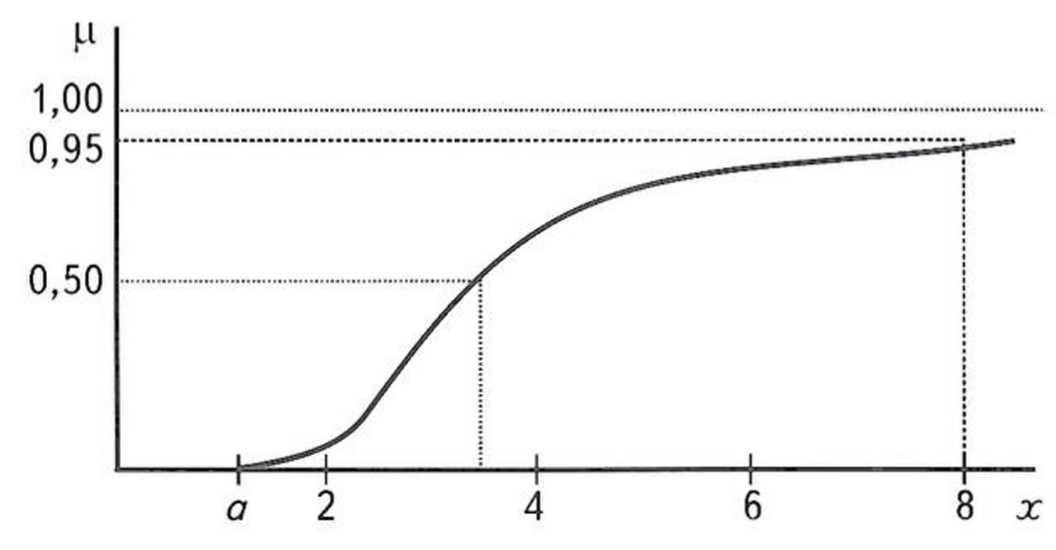
Напомним в самом общем виде содержание теории. Множество А рассматривается как нечеткое, если для него определена функция принадлежности m: A->[0,1], что для  означает: чем ближе значение m(x) к 1, тем в большей степени элемент х принадлежит рассматриваемому множеству А. Функция принадлежности непрерывна и может быть представлена графически (рис. 1). Для наших целей остановимся на функции вида

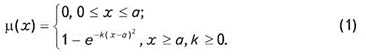
Использование функции такого вида может считаться оправданным, поскольку она соответствуют эмпирическим фактам - малый объем информации об исследуемом объекте допускает существование сколь угодно большого числа его моделей, дополнительная информация постепенно сужает альтернативность при моделировании, а после достижения некоторого порогового уровня достаточности новые порции информации не вносят существенных изменений в модель объекта. Располагая некоторым образом оцененными в численном виде объемами информации относительно объекта исследования и отложив их на оси х графика функции принадлежности в рамках понятия нечетких отношений, исследователь получает возможность оценить величину функции принадлежности. Количественный показатель объема информации, накопленной на исследуемой нефтегазоносной площади, в самом общем виде складывается из двух параметров: протяженности сейсмических профилей на единицу площади (составляющая, характеризующая геометрию напластований) и метража бурения глубоких скважин на единицу площади (составляющая, характеризующая вещественный состав пород).

На объектах, где бурение не проводилось или предполагаемая залежь не вскрыта скважинами (категория С₃), первый из двух упомянутых показателей можно рассматривать как единственный. Однако при наличии второго возникает необходимость их агрегирования. Но в силу того, что показатели характеризуют различные свойства геологической среды, операция агрегирования лишена смысла, даже если рассматриваемые параметры подвергнуты нормированию и трансформированы в безразмерные величины.

Преодоление имеющейся трудности возможно в рамках теории нечетких множеств, если каждый параметр, выраженный в виде физических показателей или каким-то другим способом, рассматривать в отдельности, используя принятый для каждого из них график функции принадлежности. Проблема построения шкалы достаточности накопленной на исследуемой территории информации не так проста, как может показаться на первый взгляд, поскольку в рассматриваемом случае предполагается существование не только нуля, но и конечного предела. Остановимся на этом вопросе подробнее.

Отождествляя геологическое пространство с понятием “множество”, исследователи обычно рассматривают некоторую часть физического пространства Земли, которое определяется как статическое в виде бесконечно большой совокупности элементов- точек, для каждой из которой можно зарегистрировать сколь угодно много свойств. В реальном геологическом пространстве может быть много пространств, отражающих то или иное физическое свойство.

Такие пространства, в отличие от реальных, принято называть формальными. Они представляют собой конечные множества точек, т.е. являются дискретными, и в конечном счете отражают степень приближения модели к реальному геологическому пространству. Понятно, что стремление к накоплению информации, характеризующей геологическое пространство, в практическом смысле должно иметь разумные ограничения, которые можно сформулировать, исходя из высказанных выше соображений: объем накопленной информации должен сводить к минимуму различия при выборе вариантов модели.

Учитывая уникальность свойств природных объектов, степень приближения модели к реальным параметрам будет зависеть от сложности его строения и потому нет никаких оснований для попыток создания некоторой универсальной шкалы. С учетом этого обстоятельства построение шкалы объемов информации с использованием физических показателей целесообразно только для территорий ограниченных размеров, характеризующихся сходными чертами геологического строения. Причем для создания такой шкалы достаточно задаться верхним порогом показателя, определив его как показатель “информационной достаточности”, исключающий существенные отклонения модели от реальной геологической ситуации. В этом случае объемы информации, характеризующие уровень неопределенности, выраженный через значение функции принадлежности, распределятся на оси абсцисс в порядке убывания от заданного верхнего предела, который в силу практической недостижимости состояния полной определенности (m(x)=1) может быть оценен значением, близким к 1 (например 0,95), до нуля по закону (1).

Если же число использованных показателей больше одного, следует использовать операцию их объединения [3]:

или

Поиски нефти из-за высокой степени неопределенности обоснованно рассматриваются как рискованная деятельность при ограниченных шансах на успех. И в этой связи полезно напомнить смысловые различия понятий “неопределенность” и “вероятность”. По мнению ведущих специалистов, употребление термина “вероятность” целесообразно при наличии некоторых знаний о статистическом поведении переменных, а термин “неопределенность” - при отсутствии таковых [5].

Теория нечетких множеств позволяет расширить представление о взаимосвязи неопределенности и вероятности, что весьма полезно при проведении вероятностного экономического анализа. В работе авторов статьи (2005) рассматривается метод, позволяющий устанавливать соответствие оценок неопределенности, выраженных посредством значений функции принадлежности и вероятностных показателей (в первую очередь - дисперсии). Для поставленной цели неопределенность, выраженная посредством функции принадлежности, преобразуется в рассеивание оценки запасов УВ, приписанной некоторому объекту. В качестве объекта, как правило, берется структура, контуры которой с некоторым приближением определены, но продуктивный пласт либо вскрыт, либо не вскрыт бурением. Отметим, что все вычислительные процедуры выполняются при условии, что месторождения, относимые к категории С₃, существуют.

Как отмечалось, информация, позволяющая рассматривать ту или иную площадь в качестве геологического объекта, вмещающего залежь УВ, сводится к двум видам: во-первых, это данные относительно геометрии объекта (преимущественно результаты сейсморазведочных работ), во-вторых, это прямые или косвенные свидетельства наличия на объекте скоплений УВ, которые можно определить общим термином “представления”. Поскольку на объекте еще не пробурены скважины, такие сведения в подавляющем большинстве относятся к категории экспертных оценок. Здесь уместно заметить, что специалисты, занятые подсчетом перспективных ресурсов, как правило, доводят “точность” своих расчетов до третьего знака после запятой, что по сути определяет вероятность результата как очень близкую либо равную единице. Но поскольку подсчет перспективных ресурсов выполняется исходя их некоторых предположений, имеющих различную степень достоверности, вероятность присутствия залежи на объекте будет значительно меньше.

Существование залежи в пределах некоторой площади оценивается в пространстве признаков, которые в одном случае можно измерить физически, а в другом - лишь прибегая к предположениям, что накладывает при составлении шкал “информационной достаточности” определенные различия. Для создания шкалы при геометризации объекта исследователи вправе воспользоваться упомянутым принципом, приняв в качестве предела некоторый объем сейсморазведочных работ, выраженный в километрах на единицу площади, обеспечивающий приемлемую достоверность геометрических построений, и, воспользовавшись выражением (1), распределить этот показатель на шкале абсцисс вплоть до 0.

Шкалу неопределенности относительно залежи УВ, выраженную через функцию принадлежности, можно создать в виде двоичной, троичной или более детальной модели оценок, не прибегая к использованию какого-либо графика функции принадлежности (Садов С.Л., Тарбаев Б.И., Захаров А.А. и др., 2005). Поскольку в подавляющем большинстве случаев, оценивая запасы УВ на объекте, исследователи располагают только косвенной информацией, разумеется, ни о какой определенности, эквивалентной вероятности, равной 1, не может быть и речи. Напомним еще раз, что в данном случае неопределенность рассматривается не в традиционном смысле (т.е. в виде ситуации, когда нет возможности определить априорную или статистическую вероятность). Здесь речь всегда идет о понимании неопределенности на базе теории нечетких множеств в виде функции принадлежности.

Принципы, заложенные в теории нечетких множеств, открывают возможность для поиска новых подходов при создании шкалы в пространстве косвенных признаков. Так, при использовании прямых показателей, характеризующих объект как геометрическую модель, предлагалось задавать некоторый порог накопленных данных, предполагающий достаточное приближение модели к реальной геологической ситуации. При использовании косвенных признаков, выраженных посредством экспертных оценок, такая возможность тоже не исключается. Можно предположить существование интегрального эксперта, располагающего всей совокупностью знаний о залежах и условиях их формирования как в общем, так и в частности, т.е. имеющем представление относительно объекта, близкое к реальности. Тогда неопределенность, выраженная посредством m(x), может быть близка к 1, но тем не менее не равна ей, и условно определена как m(x)=0,99. Это значение можно принять в качестве верхнего порога “информационной достаточности”. После принятия такой гипотезы открывается возможность для ранжирования шкалы экспертных оценок по убыванию вплоть до нулевого значения. Для практического использования графику функции можно придать ступенчатый вид с числом ступеней, отвечающим представлениям о возможности обнаружения на исследуемой территории залежей УВ, причем каждая ступень будет отвечать некоторому значению m(x). Число ступеней, исходя из разумных соображений необходимости и достаточности, можно и зафиксировать, например равным 5.

В порядке эксперимента остановимся на 5-ступенчатом графике показателя информационной достаточности (рис. 2). Каждый эксперт сможет выбрать приемлемый для себя уровень неопределенности, выражаемый функцией принадлежности

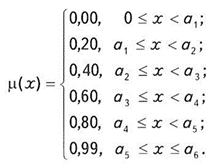
Если экспертных оценок несколько, используется операция объединения, формула которого индуктивно выводится, исходя из случая для двух оценок [3]:

Выразив неопределенность через функцию принадлежности для пространства признаков, определяющих геометрию объекта, и пространства признаков, определяющих достоверность предположений относительно оценки размеров на объекте залежи УВ, исследователь получает два показателя, выраженных в одной размерности в виде m(x). Чтобы получить значение общей неопределенности относительно оценки размеров залежи нефти или газа на объекте, целесообразно воспользоваться операцией пересечения

При проведении геолого-разведочных работ, в первую очередь при выборе площадей для заложения поисковых скважин, компании, оперирующие в сфере нефтегазодобычи, должны руководствоваться стратегиями, минимизирующими риск неоправданных финансовых потерь. Параметрами, определяющими степень такого риска, служат вероятность и дисперсия показателя наличия на объекте залежи УВ и показателя ее величины. В существующих для оценки рисков алгоритмах функция принадлежности не используется, и в этой связи возникает потребность в трансформации вычисленного значения m(x) как характеристики неопределенности величины перспективных ресурсов Q в параметры, используемые в вероятностном геолого-экономическом анализе. Естественно, что значение Q для некоторой площади, строго говоря, есть ни что иное, как случайная величина, которую в качестве предположения, имеющего вполне объективные предпосылки (специалисты, выполняющие подсчет перспективных ресурсов, ориентируются, как правило, на средние показатели), можно рассматривать как среднее некоторой гипотетической совокупности значений показателя Q. Гипотеза, отвергающая природу Q как среднего, ставит под сомнение и лишает смысла процедуры подсчета перспективных ресурсов на конкретных площадях, и в этой связи должна быть отклонена.

Понятно, что в связи с отсутствием фиксированных данных такую совокупность потребуется сформировать. Данная процедура на первый взгляд может выглядеть произволом. На самом деле это не так, поскольку при наличии среднего и начального членов совокупности, имеющих околонулевое значение и почти нулевую вероятность, эта операция по существу сводится к простой расстановке элементов с некоторой заданной частотой, т.е к выстраиванию численного ряда, где известны начало, конец, а число интервалов группирования (например, при m(x)=f(x)=0.1)) равно 24 [4]. Естественно также предположить, что в силу характера поставленной задачи, связанной с определением погрешности измерения, гипотетическая совокупность должна рассматриваться как распределенная по нормальному закону.

Любая конкретная площадь, рассматриваемая как объект с перспективными ресурсами Q, в процессе геологического обследования проходит несколько стадий приближения модели объекта к реальному состоянию, каждая из которых характеризуется соответствующим уровнем неопределенности. Последняя, как показано, при использовании теории нечетких множеств выражается в виде значений функции принадлежности m(x). По мере накопления данных значение функции принадлежности будет возрастать, стремясь к своему пределу - 1.

Аналогичная картина наблюдается и для семейства интегральных функций вероятности F[x), каждой их которых отвечает функция плотности вероятности f(x) с соответствующими параметрами колокола распределения вероятности (высотой h и стандартным отклонением s). Так, оценка запасов объекта при отсутствии информации (m(x)=0) предполагает стандартное отклонение s =±∞. В то же время при теоретически достижимой полной определенности m(x) =1 и s =0. Это крайние точки зависимости неопределенность - вероятность. Между уровнями неопределенности m(x)=0 и m(x)=1 и отвечающими им параметрами нормального распределения s = ±∞ и s =0 существует множество промежуточных состояний, где m известно, а s непосредственно определяется высотой колокола h. Если установить взаимно-однозначное соответствие между значениями функции неопределенности m и высотой h c помощью монотонно возрастающей на области определения функции , то итоговое отношение будет иметь вид . Дисперсия определяет форму кривой плотности нормального распределения, которая в одном предельном случае асимптотически стремится к оси абсцисс, а в другом - к линии, ордината которой соответствует математическому ожиданию величины объема УВ на объекте (рис. 3).

Между плотностью распределения вероятности f(x), представляемой семейством нормированных колоколов, и значениями функции принадлежности m(x) в зависимости от принятого ее графика наблюдается отчетливая связь, которая на языке множеств определится как совокупность отношений (таблица).

Приведенные в таблице отношения m(x)-f(x) могут рассматриваться как весьма распространенные, однако не обязательно универсальные. Отношения могут быть иными в зависимости от графика функции принадлежности.

Особо следует остановиться на формировании исходной гипотетической совокупности величин Q. Поскольку процесс накопления сведений об объекте относительно величины Q рассматривается как статистический, начальной его стадией может быть положена функция плотности вероятности с высотой колокола, равной 0,2. Последующие стадии вследствие поступления новой информации будут сопровождаться трансформацией начальной совокупности, стягиванием функции плотности распределения вероятности к математическому ожиданию, увеличением высоты колокола, уменьшением стандартного отклонения, выраженного в единицах группирования исходной гипотетической совокупности [4]. Все это будет находить отражение в изменении величины функции принадлежности. Таким образом, для каждой конкретной площади с оцененным значением Q, располагая значениями функции принадлежности, представляется возможным с помощью таблицы определить вероятность значения оценки перспективных ресурсов Q и погрешности, выраженные в делениях исходной шкалы.

Рассмотрим применение метода на примере геологического объекта, выявленного в пределах Печоро-Колвинской нефтегазоносной области Тимано-Печорской провинции. Объект представлен брахиантиклиналей площадью 21 км² с амплитудой 170 м и глубиной залегания 2510-2680 м, извлекаемые прогнозные ресурсы составляют 1596 тыс. т категории С₃. Плотность сейсморазведочных профилей в пределах объекта достигает 3,6 км/км².

По оценкам экспертов для площадей, входящих в состав означенной области, плотность сейсморазведочных профилей, равная 8 км/км², обеспечивает приближение модели к фактическому залеганию пластов, практически исключающее серьезные расхождения. Эту величину можно рассматривать как верхний порог шкалы физического показателя, соответствующего близкому к 1 значению функции m(x) (например, m(x)=0.95).

Значения функции принадлежности убывают в соответствии с графиком функции (1).

Из графика функции принадлежности следует, что неопределенность оценки ресурсов категории С₃, приписанных структуре, оценивается как 0,5. В экспертизе запасов залежи УВ участвовали 2 группы экспертов по 3 человека в каждой. Рассмотрев материалы, 5 экспертов пришли к мнению, что залежь существует с неопределенностью относительно ее размеров, соответствующей третьей ступени, т.е. m(x)=0.4 (рис. 4).

Лишь один эксперт высказал суждение, что утверждение залежь существует не соответствует действительности, т.е. m(x)=0. После выполнения процедуры объединения по формуле (2) получим значение неопределенности, соответствующее m(x)=0.4. Общая неопределенность, выраженная через функцию принадлежности, составит

Итак, итоговое значение неопределенности вероятности существования залежи УВ на рассматриваемой территории составляет 0,4.

Число интервалов группирования непосредственно определяется при выполнении процедуры нормирования. При m(x)=0.4 стандартное отклонение s=1 соответствует одному делению шкалы исходной совокупности или интервалу группирования, т.е. 1596 * 2/12 = 266 тыс. т. В итоге получаем значение ресурсов 1596±266 тыс. т. Базовая, минимальная и максимальная оценки ресурсов, которые учитываются при расчете экономической эффективности их освоения в странах с развитыми рыночными отношениями в недропользовании [1], составят соответственно 1596; 1330 и 1862 тыс. т.

Каждому разбиению шкалы информационной достаточности соответствует некоторое представление, которое по мере получения информации уточняется и меняется. Как правило, это способствует детализации упомянутой шкалы (см. рис. 2), увеличению ступеней ее градации. В конечном счете это ведет к уменьшению рассеивания величины ресурсов, что, несомненно, является положительным. По мнению авторов, функция информационной достаточности (см. рис. 2) является оптимальной и адекватной состоянию знаний о строении объектов, которым приписаны ресурсы категории С₃.

Литература

1. Ампилов Ю.П. Стоимостная оценка недр. - М.: Изд-во Геоинформцентр, 2003.

2. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. - М.: Мир, 1976.

3. Кофман А. Введение в теорию нечетких множеств. - М.: Радио и связь, 1982.

4. Хан Г. Статистические модели в инженерных задачах / Г. Хан, С. Шапиро. - М.: Мир, 1969.

5. Харбух Дж. Применение вероятностных методов при поисково-разведочных работах на нефть и газ / Дж. Харбух, Дж. Давтон, Дж. Дэвис. - М.: Недра, 1981.

Abstract

Oil and gas resources according to acting temporary classification relating to C3 category are determined as “oil and gas promising resources of areas prepared for deep drilling within oil and gas area and outlined by reliable for this area geological and geophysical investigations as well as not drilled-in formations of explored fields when their productivity was established in other fields of the area.” As a rule, it concerns assumed reservoirs at revealed geological objects. It means that estimates of HC volumes assigned to this object are within a certain range not excluding near-zero values when resource development is known to be unprofitable. It is obvious that for potential investor the problem of evaluating investment efficiency into additional prospecting and development of HC promising resources is solved under uncertainty conditions and the solution will depend on considering determining factors. This task is significant due to danger of oil and gas production orientation in a long-term prospect at poorly grounded indices of low exploration category of resources.

The method proposed by authors allows to solve the task of determining resource volume range considering new approaches and optimal investment strategy in oil and gas resources development what is important not only for the industry but finally for country s economy as a whole.

To solve this problem, a mathematical procedure of unclear set of numbers theory was used.

Таблица Соответствие значений функции принадлежности m(x), параметров функции распределения вероятности f(x) и интервалов группирования

m(х)	Максимальное значение f(x)	s в делениях исходной шкалы	Число делений исходной шкалы
0,20	0,20	2,00	12
0,30	0,30	1,33	12
0,40	0,40	1,00	12
0,50	0,50	0,80	12
0,60	0,60	0,67	12
0,70	0,70	0,57	12
0,80	0,80	0,50	12
0,90	0,90	0,44	12
0,99	0,99	0,40	12

Рис. 1. ГРАФИК ФУНКЦИИ ПРИНАДЛЕЖНОСТИ, ОТВЕЧАЮЩИЙ УСЛОВИЯМ ЗАДАЧИ ОЦЕНКИ ЭФФЕКТИВНОСТИ ОСВОЕНИЯ РЕСУРСОВ УВ

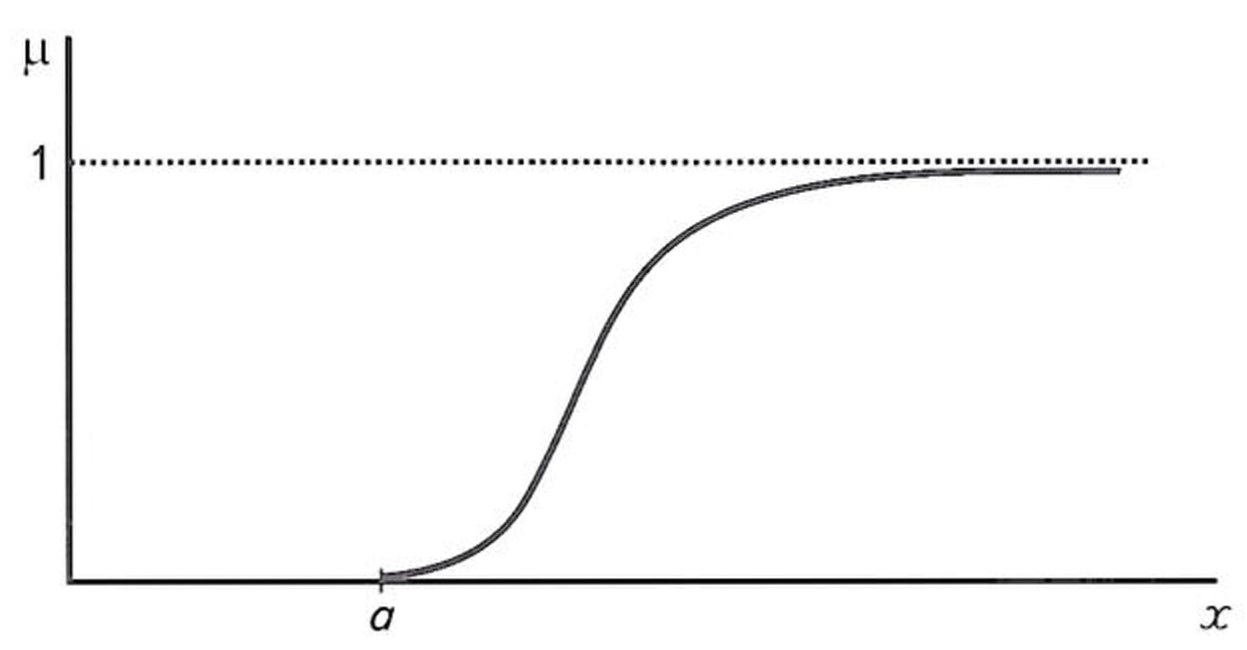
Рис. 2. ГРАФИК ФУНКЦИИ ИНФОРМАЦИОННОЙ ДОСТАТОЧНОСТИ (экспертные показатели)

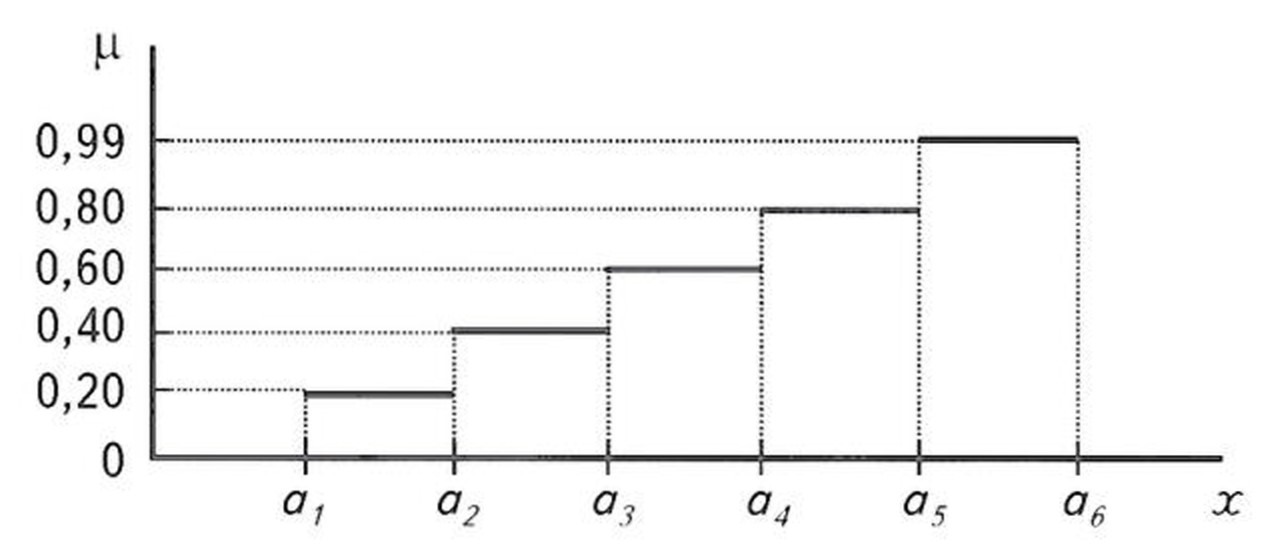
Рис. 3. СООТВЕТСТВИЕ ПОКАЗАТЕЛЕЙ НЕОПРЕДЕЛЕННОСТИ (А) И ВЕРОЯТНОСТИ (Б) В СЛУЧАЕ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

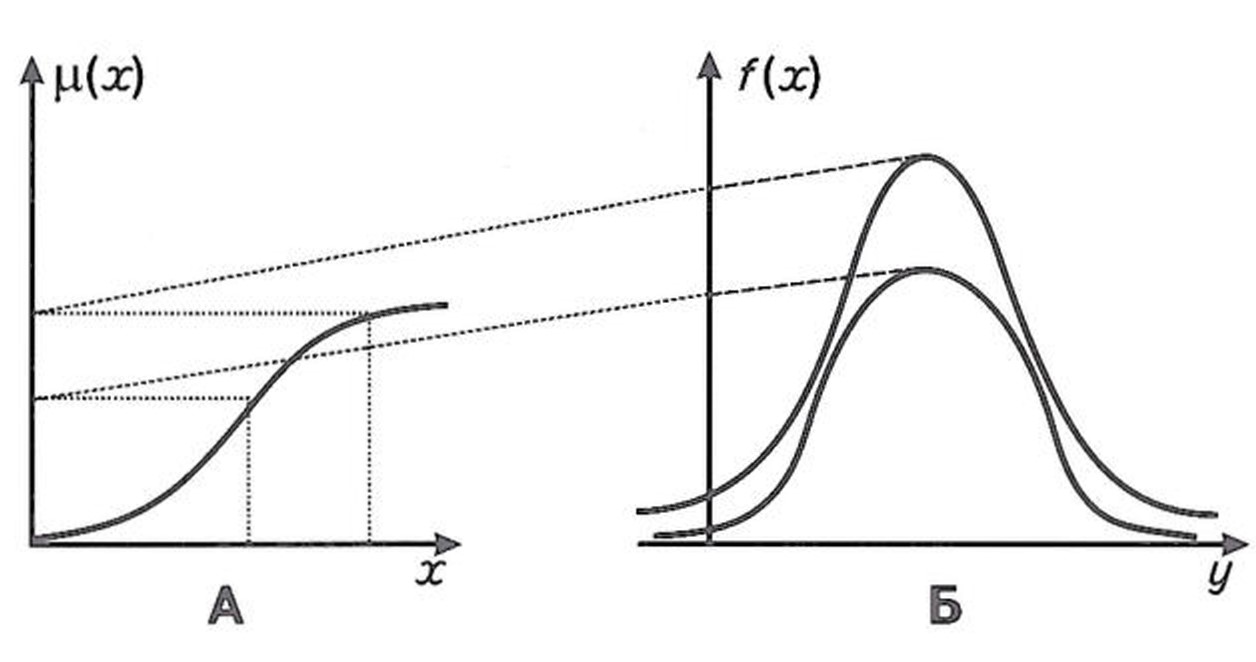
Рис. 4. ГРАФИК ФУНКЦИИ ПРИНАДЛЕЖНОСТИ ПОКАЗАТЕЛЯ ПЛОТНОСТИ СЕЙСМОРАЗВЕДОЧНЫХ ПРОФИЛЕЙ