|
© C.C. Гаврилов, В.С. Славкин, С.М. Френкель, 2006 |
ИСПОЛЬЗОВАНИЕ ДАННЫХ СЕЙСМОРАЗВЕДКИ ПРИ ТРЕХМЕРНОМ ГЕОЛОГИЧЕСКОМ МОДЕЛИРОВАНИИ (на примере месторождения Западной Сибири)
С.С. Гаврилов, В.С. Славкин (ЗАО “МиМГО”), С.М. Френкель (ВНИГНИ)
В последнее время все большее значение приобретают вопросы особенностей создания трехмерных геологических моделей для месторождений, находящихся на стадии завершения геолого-разведочного процесса [1,3]. При этом, как правило, на территории исследований пробурено ограниченное число скважин, но количество и качество сейсмических материалов обычно достаточно высокие. Естественно, что в подобной ситуации требуется максимально эффективно использовать результаты не только кинематической, но и динамической интерпретации данных сейсморазведки.
Рассмотрим методы “традиционного” использования результатов динамической интерпретации данных сейсморазведки, а также предложенную авторами статьи альтернативную методику. Преимущества предлагаемой методики, на наш взгляд, становятся очевидными при построении трехмерных моделей для резервуаров с высокой вертикальной и/или латеральной изменчивостью. Основным ее достоинством является то, что она может базироваться на результатах практически любого метода интерпретации данных как 3D, так и 2D сейсмических данных.
Современные комплексы интерпретационной обработки, интенсивно развивающиеся во всем мире, позволяют рассчитывать множество численных параметров, характеризующих форму сейсмического волнового поля (сейсмических атрибутов), и проводить их интерпретацию с реализацией алгоритмов многомерных зависимостей. Естественно, что программные пакеты, направленные на создание трехмерных геологических моделей, с большим успехом позволяют учитывать полученные при интерпретационной обработке данные. Однако здесь существует ряд ограничений, о которых зачастую умалчивается.
Во-первых, программы трехмерного моделирования эффективно (напрямую) используют параметры (атрибуты), рассчитанные по данным трехмерной сейсморазведки [2, 4].
Во-вторых, как известно, эффективность использования сейсмических атрибутов при трехмерном моделировании пропорциональна мощности моделируемого объекта. Если мощность моделируемого объекта во временном поле достаточно высока (т.е. объект характеризуется несколькими фазами сейсмического волнового поля), то применение “куба” сейсмических атрибутов может дать хорошие результаты. Если же временная мощность моделируемого объекта <15 мс (т.е. менее одной фазы сейсмической записи), то эффективность применения сейсмических атрибутов мала. Особенно остро эта проблема стоит при построении моделей относительно маломощных (<40 м) пластов с сильной вертикальной литологической изменчивостью.
Большинство объектов, вовлекаемых в разработку или находящихся на стадии доразведки, в том числе в Западной Сибири, характеризуются крайне высокой степенью вертикальной литологической неоднородности. Учет частичной или значительной вертикальной флюидодинамической разобщенности пласта позволяет коренным образом пересмотреть перспективы отдельных объектов, а иногда и месторождений. В связи с этим вопрос использования результатов динамической интерпретации данных сейсморазведки при построении трехмерной геологической модели месторождения приобретает новую актуальность.
Интерпретация данных сейсморазведки непременно опирается на детальное изучение всего комплекса скважинных данных. Поэтому основой для нее, как правило, является геолого-геофизическая типизация разрезов пласта по точкам скважин. Важно отметить, что при этом толщина интервала исследования ограничивается разными соображениями - как геологическими (макроцикл, характеризующийся унаследованным развитием), так и технологическими, связанными с особенностями применяемых методов динамической интерпретации. Желательно, чтобы типизация имела очевидное и понятное генетическое истолкование - это намного повышает ее надежность и позволяет в результате исследований получить карту фациальных типов пласта.
При подобном подходе для повышения достоверности обычно проводится комплексирование нескольких технологий интерпретации или используется интегральная характеристика сейсмической записи. Примером подобной характеристики, которая уже несколько лет с большим успехом применяется в ЗАО “МиМГО”, может являться спектральная частотно-временная трансформация, получаемая в процессе спектрально-временного анализа (СВАН) сейсмической записи (Славкин В.С. и др., 1999; Славкин В.С., 1999). Данная методика основана на спектральной частотной развертке сейсмического сигнала и впервые предложена И.А. Мушиным (1990) как метод исследования строения разреза в межскважинном пространстве. Для численных расчетов и анализа используется набор спектрально-временных параметров. Важной особенностью методов прогноза, базирующихся на численном представлении этих параметров, служит оценка не каждого параметра в отдельности, а их взаимоотношения в факторном пространстве. Таким образом, в применяемой методике, с одной стороны, достигается именно комплексный анализ параметров сейсмической записи, а с другой - необходимая для каждого конкретного случая прогноза расчлененность (кластеризация) параметров. Собственно результатом работы в интерпретационном наборе программ методики СВАН являются карты распространения типов разреза, выделенных согласно их типизации.
Полученная карта означает, что согласно модели:
свойства пласта достаточно выдержаны в пределах зон развития каждого отдельного типа разреза;
свойства пласта в пределах зон каждого из типов разреза характеризуются заметным сходством со свойствами этого пласта в точках скважин, входящих в данных тип;
свойства пласта заметно меняются вблизи границ зон распространения типов разреза.
Еще раз заметим, что итоговая прогнозная карта распространения типов разреза в принципе может быть получена по результатам применения целого набора различных методов интерпретации.
Использование именно результирующей карты при построении геологических моделей объектов очевидно, однако ее применение в трехмерных моделях - достаточно редкое явление. Это объясняется тем, что специального встроенного инструмента для этой процедуры не предусмотрено ни в одном из программных комплексов трехмерного моделирования. Однако при этом имеющиеся инструменты различных комплексов все же позволяют это сделать. Следовательно, важнейшим вопросом в данном направлении является выработка общих методических приемов, которые могли бы применяться во всех системах трехмерного моделирования.
Рассмотрим предлагаемую методику на примере одного из участков Западной Сибири.
В разрезе верхнеюрских отложений изучаемого месторождения выделяются два песчаных пласта: ЮВ11 и ЮВ12, из которых продуктивен только первый пласт. На основе анализа геолого-промысловых данных в этом пласте выделено три типа разреза (рис. 1).
К I типу (Обычно тип разреза пласта, характеризующийся лучшими фильтрационно-емкостными параметрами, называют первым (“самым лучшим” на территории исследований), далее увеличение номера соответствует ухудшению фильтрационно-емкостных свойств пласта.) отнесены разрезы скв. 1, 2, 5, 8, в которых пласт ЮВ11 представлен от мелкозернистых до крупнозернистых песчаниками с закономерным увеличением зернистости вверх по разрезу (рециклитовое строение). Песчаники этого типа формировались на северном погруженном склоне крупного палеоподнятия. Это обеспечило наибольшие общие толщины пласта (14,2-19,0 м), а также высокие эффективные толщины (9,7-14,5 м). Пористость в верхней части пласта составляет 17,0-19,6 %, в нижней - 12,4-15,4 %.
Высокая гидродинамическая активность при осадконакоплении способствовала интенсивному перемыву обломочного материала, вымыванию тонких алевритовых и глинистых частиц и улучшению сортировки. Все это обеспечило высокие емкостные и фильтрационные свойства коллекторов.
Во II тип разреза объединены скв. 3, 4, 6, 7, 9, 10, 14. Пласт ЮВ11 в этих скважинах характеризуется меньшими, чем в I типе толщинами (общими от 6,8 до 11,0 м и эффективными от 5,0 до 7,8 м), коэффициент пористости составляет 16,7-19,1 %. Коллекторы представлены слабосцементированными крупно-, средне-, мелкозернистыми песчаниками. Для скважин этого типа разреза характерно как рециклитовое, так и репроциклитовое строение.
К III типу разреза отнесена скв. 12, которая характеризуется достаточно низким значением эффективных толщин (5,2 м), среднее значение пористости также гораздо ниже (15,7 %). Низкими являются также фильтрационные свойства - проницаемость по ГИС в этой скважине изменяется от 0,0016 до 0,0204 мкм2 (среднее - 0,0111 мкм2). При испытании в эксплуатационной колонне из пласта ЮВ11 было получено 3,62 м3/сут воды и 0,48 м3/сут нефти при депрессии 10,7 МПа. По данным исследования керна пласт ЮВ11 представлен мелко- и среднезернистыми уплотненными песчаниками. Вероятно, ухудшенные свойства коллекторов в районе скв. 12 связаны с тем, что к востоку существовала зона “экрана”, через которую был затруднен привнос песчаного материала. Таким образом, отложения II и III типов разреза формировались в условиях своеобразной “лагуны”, в которую был затруднен привнос песчаного материала, а гидродинамическая активность среды была достаточно низка и не обеспечивала перемыва и сортировки песчаного материла.
Поскольку пласт ЮВ11 имеет небольшие мощности, а возможности сейсморазведки не позволяют осуществлять прогноз в таких небольших интервалах, при типизации разреза верхнеюрских отложений в интервал был включен нижележащий пласт ЮВ12.
Пласт ЮВ12 в пределах исследуемой территории развит в песчаных фациях только в скв. 3, 7, 11, где он имеет, очевидно, баровый генезис (монолитный пласт, рециклитовое строение, низкая расчлененность, высокие фильтрационно-емкостные свойства), в остальных скважинах пласт представлен алевролито-глинистыми отложениями.
На территории исследований была проведена двухмерная сейсморазведка. Прогнозирование свойств разреза в межскважинном пространстве было осуществлено с использованием методики СВАН (рис. 2).
Тип разреза I, характеризующийся высокими значениями эффективных толщин пласта и высокими значениями пористости, распространен в северной части территории. Тип разреза II, имеющий меньшие эффективные толщины, но достаточно высокую пористость, распространен в центральной и юго-западной частях территории. Тип разреза III, где для пласта ЮВ11 характерны низкие значения толщин и пористости, формирует зону сложной конфигурации в юго-восточной части территории. Выявленные закономерности распространения свойств пласта должны быть учтены в трехмерной геологической модели.
В отличие от относительно слабой латеральной изменчивости в данном случае продуктивный пласт сильно изменчив по вертикали. На фоне общего регрессивного строения в пласте отмечаются уровни достаточно частого переслаивания проницаемых песчаных и непроницаемых алевролито-глинистых отложений. Особенно это характерно для II типа строения пласта, который образовался в условиях изменчивой активности среды. Помимо этого в разрезе встречаются реперные пропластки вторичных известняков (сильно известковых песчаников и алевролитов), которые, по-видимому, маркируют уровни перерывов осадконакопления на значительной территории.
Первым шагом при построении трехмерной геологической модели является построение литофациальной модели изучаемого объекта. Собственно, уже на этой стадии прогнозное распределение типов разреза должно найти максимальное отображение.
Ясно, что границы зон распространения типов разреза не должны представлять собой резко выраженные плоскости, внешне схожие с разрывными нарушениями, вдоль которых мгновенно изменяются свойства пласта (в том числе литологические) - они должны определять плоскость, характеризующую максимальный градиент изменения свойств. При этом резкой границы в самих свойствах быть не должно (кроме тех случаев, когда это предусматривается геологической моделью). Если мы попытаемся провести распределение параметра, кодирующего литологический состав пород отдельно в пределах участков распространения различных типов разреза, то неизбежно столкнемся с проблемой резкости границ (рис. 3). Естественно, гидродинамическая модель, основанная на такой литофациальной модели, не выдержит никакой критики. Это означает, что распределение значений кривой литофациальных типов (В программных пакетах трехмерного моделирования понятия литологический и фациальный типы часто синонимизируются. Это объясняется задачами построений и, как правило, весьма ограниченным набором литологических типов, выделяемых при интерпретации пласта. Авторы статьи в этом случае используют термин “литофациальный тип”.) должно производиться не в пределах каждого типа отдельно, а по всей модели одновременно. Естественно, что “независимое” стохастическое распределение в данном случае не дает необходимого результата - свойства в пределах типов не будут выдержаны. Требуется распределение с учетом некоторого контролирующего весового параметра.
Рассмотрим к каким последствиям может привести прямое использование простого весового коэффициента (т.е. коэффициента, значение которого определяет принадлежность каждой конкретной ячейки модели к определенному типу).
Это тем более интересно, что аналогичным образом используются “кубы” различных сейсмических атрибутов, поэтому их прямое использование может также привести к подобным последствиям.
Речь идет о построении литофациальной модели одним из методов моделирования, позволяющим учитывать внешние данные в качестве трендов или весовых функций. Наиболее известными среди них являются методы Collocated Cokriging, Kriging with external drift, Bayesian Updating [2]. Настройка вариограмм должна соответствовать основам геологической модели - быстрая изменчивость по вертикали, относительная выдержанность по латерали. Все многочисленные реализации модели, созданной по описанной схеме, характеризуются общей чертой - на некотором удалении от скважин вертикальная расчлененность пласта начинает уменьшаться. Важно отметить, что подобное явление не вызвано некорректностью вариограмм или каких-либо других настроек распределения. Это легко проверить, если построить ряд реализаций этой же модели с сохранением всех настроек вариограмм, но без использования весового коэффициента (или сейсмических данных) в качестве тренда.
С нашей точки зрения в данном случае существуют две технологии решения поставленной задачи: 1 - расчет параметров вероятности нахождения каждого конкретного литологического типа в конкретной ячейке; 2 - имеющаяся в первом приближении 3D-литофациальная модель. Оба данных подхода - это несколько отличные способы наложения ограничений на стохастическое распределение. В первом случае при распределении свойства мы используем “кубы” вероятностей наличия каждого конкретного литофациального типа в каждой конкретной ячейке, во втором случае мы имеем один из результатов свертки этих “кубов” вероятностей. Несмотря на общую идею, оба решения предъявляют различные требования к математическому аппарату трехмерного моделирования. Первый способ более сложный, но более “управляем”, т.е. он позволяет контролировать построения на всех стадиях. Второй - более “скрытый”, но зато более быстрый и простой.
Первый путь решения подразумевает расчет обобщенной вероятности нахождения каждой из литофациальных единиц в пределах каждого типа. Наиболее удобной для использования в данном случае является двухмерная зависимость вероятности нахождения литофациальной единицы от удаления от кровли пласта (h). Она определяется по имеющимся скважинам. Расчет этой величины кажется во многом схожим с получением вариограмм, но результат отличен - мы сразу же получаем вариограмму, в разной степени привязывающую литофациальную единицу к разному вертикальному (стратиграфическому) уровню в пласте,
![]()
где z - расстояние от кровли пласта до анализируемой ячейки.
Число значений h определяется числом литофациальных единиц i и числом анализируемых типов разреза j и равно ij. Функция h является разверткой программы геолого-стратиграфического разреза (ГСР), которая получается для всех скважин определенного типа разреза. Значения h равномерно распределяются по объему соответствующих подмоделей, отвечающих районам распространения различных типов разреза. На созданной таким образом основе путем объединения для каждого литофациального типа вероятности его нахождения в ячейке в единую модель происходит создание трехмерной функции (модели) вероятности нахождения каждого конкретного литофациального типа во всех ячейках модели. При создании литофациальной модели данные функции используются в качестве весовых для каждого соответствующего литотипа.
Как видим, процедура достаточно объемна, а главное, может быть реализована только в тех программных продуктах, где поддерживается возможность использования отдельных весовых функций для каждого литотипа.
Второй путь можно назвать “квазистохастическим” в отличие от первого “квазидетерминистического”. Его преимущество заключается в том, что он может использоваться в любых программных комплексах трехмерного моделирования и базироваться на всех основных алгоритмах распределения свойств, учитывающих зависимости (Collocated Cokriging, Bayesian Updating, Kriging with external drift и др.).
Первый этап построения модели при втором подходе подразумевает начальное распределение свойства по всей модели только на основе скважинных данных. Таким образом формируется априорное трендовое распределение. Настройки метода распределения должны быть такими, чтобы получившаяся картина в целом была бы приближена к геологической модели (рис. 4, А). Следующий шаг - распределение свойств пласта в пределах территорий распространения каждого из типов разреза в отдельности. Подобное распределение проводится на основе только тех скважин, разрезы которых входят в рассматриваемый тип строения пласта. Распределение проводится одним из методов, позволяющим опираться на трендовое распределение, в качестве тренда используется распределение, выявленное на первом этапе. Полученные модели распределения свойств в зонах распространения всех типов разреза объединяются в единую модель для всей территории. В принципе, это распределение уже на данной стадии может удовлетворять предъявляемым требованиям. Однако, если требуются некоторые исправления, то их следует сделать в “ручном” режиме и провести повторное распределение свойства по всей территории исследований, опираясь на отредактированную модель (см. рис. 4, Б, В). При этом степень соответствия новой модели трендовой будет определяться коэффициентом зависимости в используемом уравнении.
Для оценки результатов предлагаемой методики построим три модели различными способами: 1 - только по скважинным данным; 2 - с “традиционным” использованием сейсмического “куба” в виде тренда; 3 - по предлагаемой методике с использованием технологии построения модели на основе ГСР (рис. 5).
Рассмотрим, к чему приводит неучет одной из скважин при построении модели одним из трех рассматриваемых способов. Все три модели были построены без участия скважины N. После составления трех трехмерных моделей искомая скважина была загружена в проект. Это имитирует вариант бурения разведочной скважины по результатам построения геолого-геофизической модели участка. Естественно, в данном случае подразумевается, что интерпретация сейсмических данных позволила в целом правильно спрогнозировать характер разреза пласта в точке, намеченной к бурению. На рис. 5, А представлена одна из наиболее удачных, на наш взгляд, реализаций модели, построенной на основе только скважинных данных. Рисунок 5, Б представляет вариант модели, построенной при “традиционном” (т.е. в качестве тренда, или “подложки”) использовании результатов динамической интерпретации данных сейсморазведки.
На рис. 5, В, в свою очередь, показан фрагмент модели, построенной по предлагаемой методике. Настройки параметров алгоритмов распределения примерно одинаковы и направлены на максимальное соответствие моделей друг с другом и с геологическими представлениями. Данные “новой пробуренной” скважины неудовлетворительным образом вписались в модель, опиравшуюся только на скважины - строение разреза определялось либо соседними скважинами, либо - стохастически-случайно (см. рис. 5).
Эта скважина не очень хорошо подтвердила бы модель с традиционным использованием сейсмических атрибутов - прогнозируемая вертикальная расчлененность пласта была намного ниже, чем оказалось в действительности. Наилучшим образом данная скважина входит в модель, построенную авторским методом. Для сравнения, на рис. 5, Г приведена модель, построенная с учетом контрольной скважины.
Преимущества предлагаемого подхода к использованию данных сейсморазведки заключаются в следующем.
Во-первых, этот подход позволяет в полной мере использовать любые прогнозные карты, а также фациальные карты любой детальности и сложности, полученные по любой методике на основе как трехмерной, так и двухмерной сейсмической съемки, а также скомпилированные по результатам прогноза различными методами.
Во-вторых, он включает независимый расчет размеров неоднородностей пласта для территории распространения каждого геологического типа разреза на изучаемой территории, что методически более правильно.
В-третьих, прекрасно сочетаясь с любыми другими методами определения размеров и положения горизонтальных неоднородностей пласта, он позволяет в необходимой мере сохранять особенности вертикального строения тонкослоистых резервуаров.
И наконец, в-четвертых, данный метод не является детерминизированным и позволяет включать в расчеты элементы стохастики на любых стадиях в любых требуемых объемах.
Таким образом, сделан первый шаг на пути создания методологии и технологии использования карт распространения типов разреза (фациальных карт) при трехмерном геологическом моделировании. Существует еще ряд вопросов, которые будут решены по мере продолжения работы над этой задачей.
Литература
1. Богатырев А.А. Некоторые вопросы геологического моделирования залежей на различных стадиях ГРР / Нефтегазоносные системы осадочных бассейнов/ Тез. докл. 8 конференции “Новые идеи в геологии и геохимии нефти и газа”. - М.: Изд-во ГЕОС, 2005.
2. Дюбрул Оливье. Использование геостатистики для включения в геологическую модель сейсмических данных. - Изд-во: EAGE, 2002.
3. Емельянова Н.М. Агрегирование оценок запасов нефти и газа при детерминированном и вероятностном методах подсчета / Н.М. Емельянова, В.И. Пороскун // Геология, геофизика и разработка нефтяных и газовых месторождений. - 2005. - № 8.
4. Методические указания по созданию постоянно действующих геолого-технологических моделей нефтяных и газонефтяных месторождений. - М.: Изд-во ВНИИОЭНГ, 2003.
5. Chakraborty A. a. Frequensy-time decompositions of seismic data using wawelet-based methods / A. Chakraborty, D.Okaya // Geophisics. - 1965. - N 60.
The article is devoted to actual problem of using results of seismic prospecting data interpretation in creating three-dimensional geological models of oil fields. The authors propose a new method of using the obtained maps of geological types of section or facial maps in lithofacial cubes in three-dimensional geological models.
For most full using of prognostic maps in different systems of three-dimensional simulation two alternative technologies were elaborated. The first one is suggested for object simulation, the second - in stochastic indicator simulation. Advantages of the suggested approach become obvious in elaborating oil pools models in layers with high vertical and complicated lateral variability. Realization of suggested methodology is presented on the example of Upper Jurassic layer YuV,1 of one of West Siberian fields. Proposed methodologies and technologies of using seismic prospecting data in creating three-dimensional geological models present an obvious interest because they open a new possibility to use a wide spectrum of prognostic maps. The authors did the first step on the way of elaborating methodology and technology of using maps of section type distribution in three-dimensional geological simulation.
Рис. 1. ЭЛЕКТРОМЕТРИЧЕСКИЕ ОБРАЗЫ ГЕОЛОГИЧЕСКИХ ТИПОВ РАЗРЕЗА ПЛАСТА ЮВ11
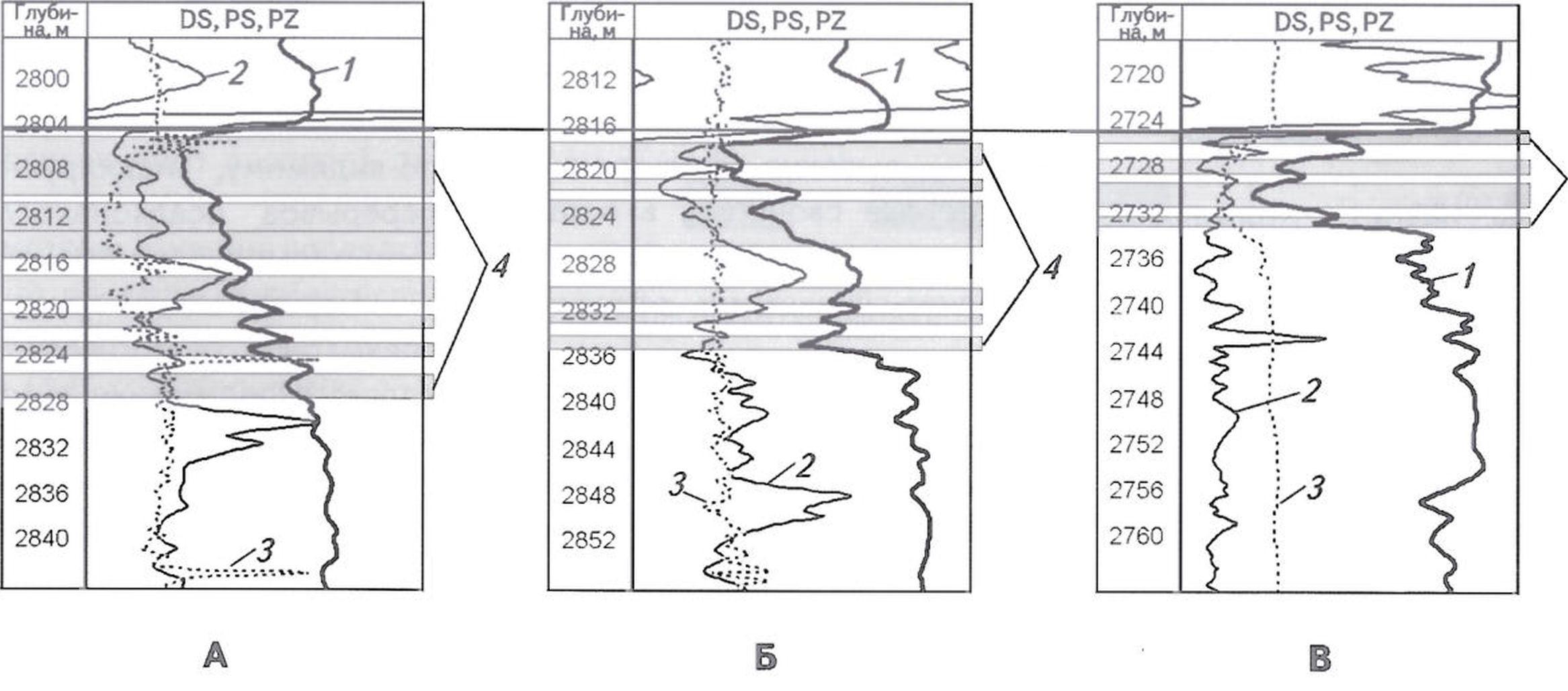
1ип разреза: А-I (Нэф = 15,4 м, Кп = 18,7 %), Б-II (НЭф = 9,7 м. Кп = 17.0%). В-III (Нэф = 5.2 м. Кп = 15.7 %); каротажные кривые: 1 - ПС, 2 - КС, 3 - ДС: 4 - эффективные пропластки
Рис. 2. КАРТА РАСПРОСТРАНЕНИЯ ТИПОВ РАЗРЕЗА ПО ДАННЫМ СВАН
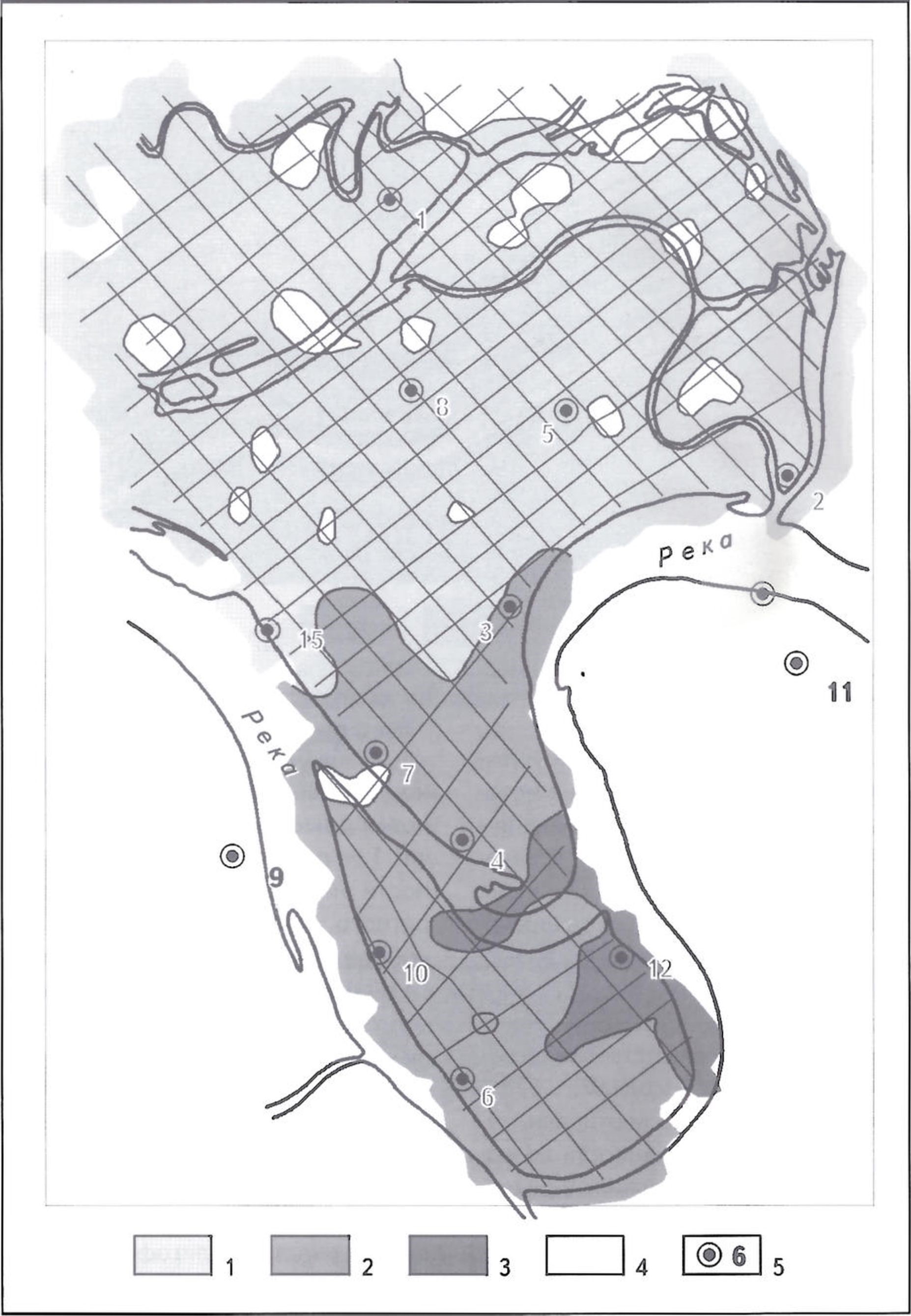
Области распространения геологических типов разреза: 1 - I. 2- II. 3- II, 4- неизвестного: 5 - скважины
Рис. 3. РЕЗКАЯ ГРАНИЦА, ВОЗНИКАЮЩАЯ ПРИ ПОПЫТКЕ ОБЪЕДИНЕНИЯ ПОДМОДЕЛЕЙ, ПОСТРОЕННЫХ ОТДЕЛЬНО ПО УЧАСТКАМ РАСПРОСТРАНЕНИЯ КАЖДОГО ИЗ ТИПОВ РАЗРЕЗА
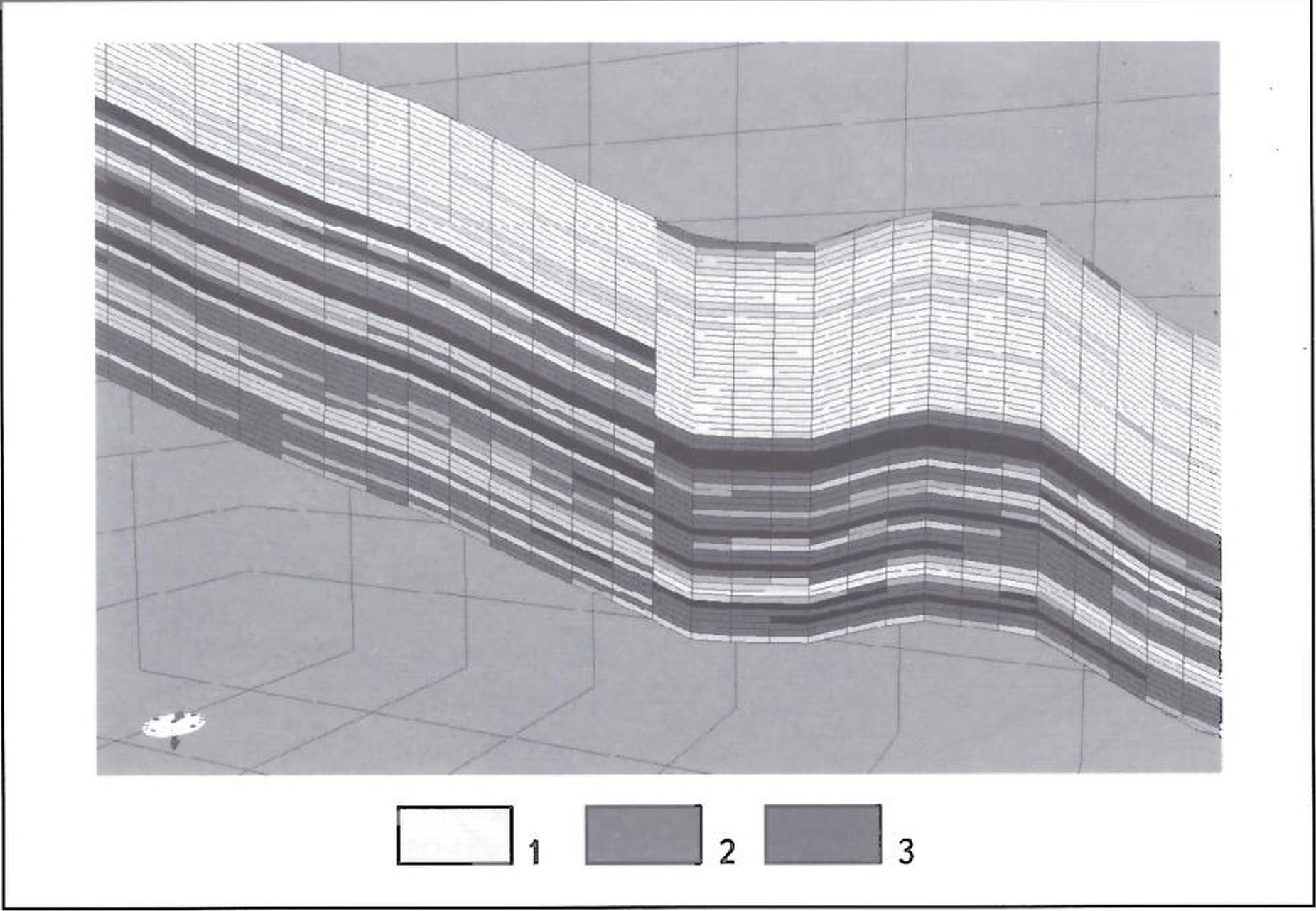
1 - песчаники; 2- алевролиты; 3- глины
Рис. 4. ПОСТРОЕНИЕ ЛИТОФАЦИАЛЬНОИ МОДЕЛИ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНОГО ИСПОЛЬЗОВАНИЯ ТРЕНДОВ

А - исходный общий тренд. Б- литофациальная модель на основе исходного тренда с использованием карты типов разреза, В - скорректированная литофациальная модель; 1 - песчаники. 2 - алевролиты, 3 - глины, 4 - известняки
Рис. 5. ФРАГМЕНТЫ ЛИТОФАЦИАЛЬНОЙ МОДЕЛИ В РАЙОНЕ КОНТРОЛЬНОЙ СКВАЖИНЫ
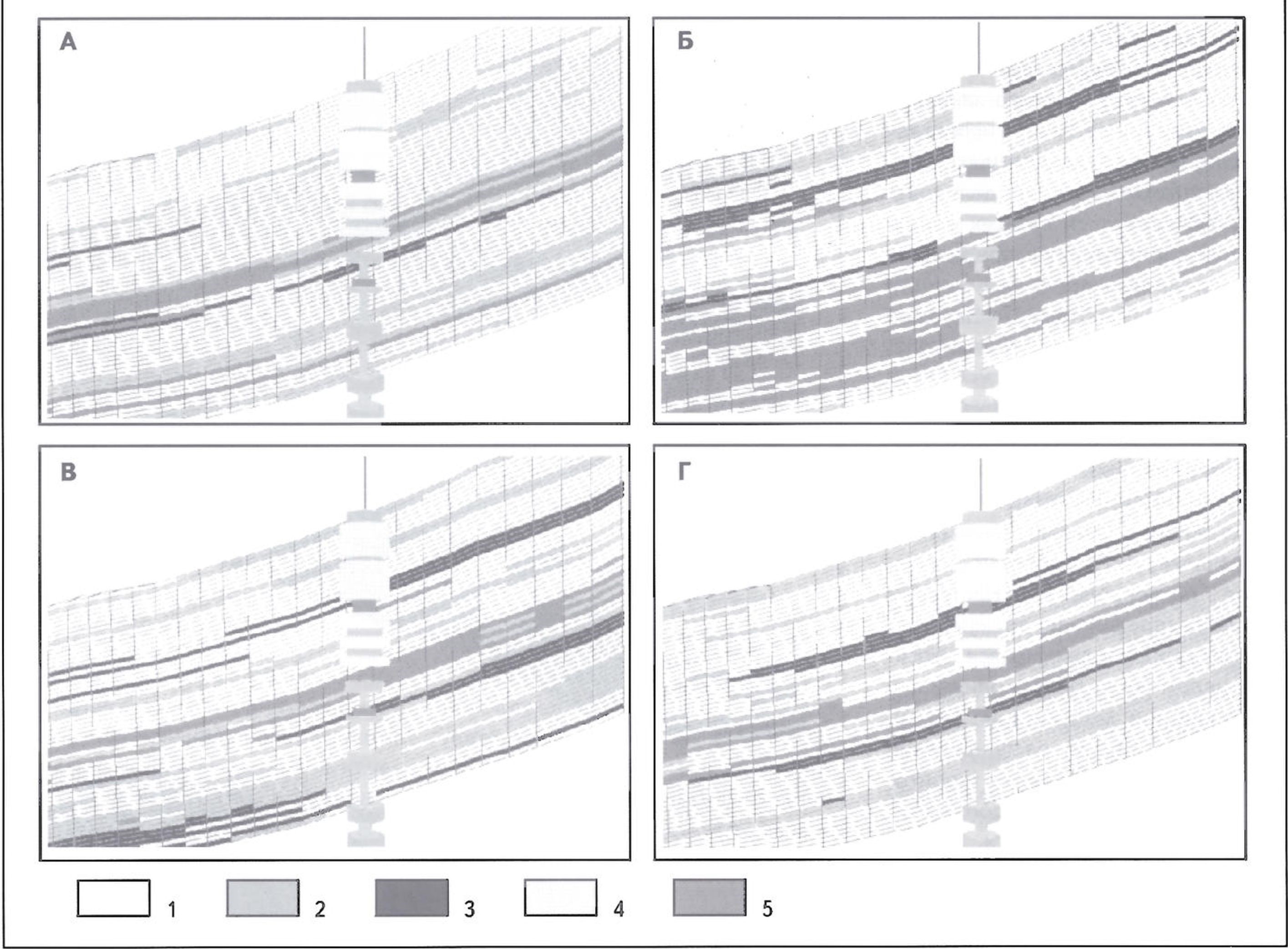
А - построенной только на скважинных данных. Б- с использованием сейсмического тренда 3D, В - по предлагаемой методике. Г- с учетом контрольной скважины; 1 - породы-коллекторы (песчаники); породы-неколлекторы: 2 - алевролиты, 3 - карбонаты (известняки), 4 - глинистые алевролиты, 5 - глины