К оглавлению	УДК 539.217 552.5 553.982 (471.4) (471.503) (471.505)
	А.В. Белов

О РАСПРЕДЕЛЕНИИ ПРОНИЦАЕМОСТИ В ОСНОВНЫХ ПРОДУКТИВНЫХ ГОРИЗОНТАХ НЕФТЯНЫХ МЕСТОРОЖДЕНИИ УРАЛО-ПОВОЛЖЬЯ

Выяснению закона распределения проницаемости в продуктивных горизонтах нефтяных месторождений посвящен ряд работ как в отечественной, так и в зарубежной литературе [1, 3, 4, 7, 8, 9]. Однако авторы большинства из этих работ ограничиваются общими, слабо аргументированными предположениями о возможности применения того или иного известного закона распределения к изучению неоднородности пластов по проницаемости. Основным аргументом при этом обычно является чисто внешнее, иногда весьма отдаленное, сходство кривой плотности вероятности того или иного закона распределения и гистограммы проницаемости или некоторой ее функции. Более детального анализа, основанного на сопоставлении фактических средних величин, средних квадратических отклонений и коэффициентов вариации с расчетными, получаемыми по параметрам предлагаемого закона распределения, как правило, не производится.

Несколько своеобразна по подходу к решению данной задачи и в значительной степени подкреплена фактическим материалом работа М.М. Саттарова [3], в которой автор пытается теоретически обосновать закон распределения проницаемости в терригенных отложениях. В качестве отправного момента при выводе распределения проницаемости М.М. Саттаров использует распределение Максвелла, которому, как он считает, подчинено распределение радиусов песчинок в породе. Предполагая наличие функциональной связи между размерами радиусов песчинок и проницаемостью, он приходит к аналитическому выражению распределения проницаемости путем замены переменного в распределении Максвелла.

Распределение проницаемости, предложенное М.М. Саттаровым, быстро завоевало популярность у исследователей, занимающихся вопросами изучения неоднородности нефтеносных пластов. Вместе с тем в адрес этого распределения были высказаны и критические замечания, предостерегающие против его использования для решения практических задач [6]. Не вдаваясь в подробный разбор этого распределения, необходимо все же отметить, что в некоторых отношениях оно неудобно для изучения. В частности, будучи сильно асимметричным, это распределение не позволяет применять к изучению проницаемости такой важный раздел математической статистики, как дисперсионный анализ.

С теоретической точки зрения распределение проницаемости может быть аналитически выражено бесчисленным количеством различных формул, если при их выводе использовать известные распределения величин, находящихся в функциональной зависимости с проницаемостью. С этой точки зрения определенный практический смысл представляет преобразование распределения проницаемости в функционально- нормальное распределение, т.е. отыскание такой функции проницаемости, распределение которой подчинялось бы нормальному закону. Для этого на материале более чем 5000 лабораторных определений абсолютной проницаемости по керну из девяти залежей нефти Урало-Поволжья, приуроченных к терригенным отложениям нижнего карбона и девона, нами эмпирическим путем изучались распределения различных простых функций величины проницаемости. В результате было установлено, что наилучшее приближение к нормальному закону распределения дает функция , где к - проницаемость в д. При анализе использовались определения проницаемости, замеренные по воздуху в направлениях, как параллельном, так и перпендикулярном напластованию. Как показали результаты сопоставления, при тех размерах образцов керна, которые применяются в настоящее время при массовых измерениях проницаемости в лабораториях, разница в средних величинах проницаемости образцов, ориентированных вкрест напластованию и параллельно ему для горизонтов, характеризующихся средней проницаемостью более 1 д, практически не ощутима. Для горизонтов с меньшими средними значениями проницаемости эта разница возрастает по мере уменьшения средней проницаемости горизонта. Однако и в этом случае при одинаковом количестве тех и других образцов средняя проницаемость, подсчитанная по всем образцам, отличалась от средней проницаемости образцов, ориентированных параллельно напластованию, не более чем на 7%.

Доля образцов, ориентированных параллельно напластованию, для различных залежей оказалась неодинаковой и колебалась от 33,0 (Арлан) до 100% (Муханово). Такая разнородность фактического материала несколько снижает качество проводимых исследований, однако, принимая во внимание сказанное выше, она не может существенно повлиять на конечные результаты.

В процессе анализа было замечено, что распределение величины  лучше согласуется с нормальным законом, если учитывать не все образцы, а лишь те, которые выше некоторой величины, например, 10 мд, исключая образцы с проницаемостью до 10 мд. Исключение этих образцов из расчетов, по нашему мнению, вполне правомерно так как, согласно работе [2], породы с проницаемостью ниже 10 мд не являются коллекторами в условиях, аналогичных девонским залежам Татарии.

С еще большим основанием это можно сказать про нижнекаменноугольные терригенные отложения Урало-Поволжья потому, что средняя проницаемость последних и вязкость нефти, содержащейся в них, обычно выше, чем в девонских залежах.

Как известно из теории вероятности, нормальный закон полностью характеризуется двумя параметрами - средним арифметическим х₀ и средним квадратическим отклонением σ. Установив, что величина  распределяется по нормальному закону, нетрудно найти функцию распределения, математическое ожидание, среднее квадратическое отклонение, коэффициент вариации, моду и медиану распределения проницаемости, используя для этого параметры х₀ и σ.

Так, функция распределения проницаемости F (к) выразится формулой:

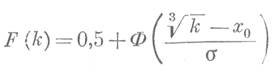
где

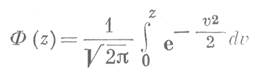
является нормированной функцией Лапласа; х₀ - среднее арифметическое величины; σ – среднеквадратическое отклонение величины

Значения функции Лапласа табулированы и приводятся во многих пособиях по математической статистике [4].

Математическое ожидание или теоретическое значение средней арифметической проницаемости определяется по формуле:

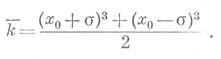
Медианное значение проницаемости равно:

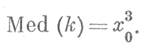
Мода или наиболее вероятное значение проницаемости определяется по формуле:

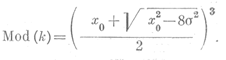
Следует отметить, что некоторые продуктивные горизонты характеризуются отсутствием моды или, точнее, наиболее вероятное значение проницаемости соответствует минимальному ее значению (например, в бобриковском горизонте на Арланской площади).

Среднее квадратическое отклонение проницаемости σ_k наиболее просто определяется по параметру U, равному σ/x₀:

И, наконец, коэффициент вариации проницаемости определяется как:

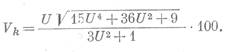
Для проверки соответствия распределения проницаемости приведенному выше закону применен графический метод, основанный на использовании так называемых диаграмм квантилей. В случае соответствия фактических данных проверяемому закону распределения точки на диаграмме квантилей располагаются по прямой линии. Незначительные отклонения точек от прямой обусловливаются случайностью выборки. Основу диаграмм квантилей, изображенных на рисунке, составляет шкала накопленных частостей или функции распределения нормального закона, нанесенная по оси ординат. По оси абсцисс нанесены две шкалы: одна, равномерная (шкала х), представлена в единицах, другая, неравномерная, выражена в единицах проницаемости (в д). Наличие двух шкал по оси абсцисс значительно упрощает расчеты. Так, пользуясь шкалой проницаемости, можно непосредственно наносить накопленные частости проницаемости, избегая определения накопленных частостей величин

Шкала х, выраженная в единицах служит для графического определения параметров х₀ и σ, имеющих размерность

Параметр х₀ определяется графически так: через нанесенные на диаграмму точки накопленных частостей проводится прямая линия. На прямой отыскивают точку, соответствующую накопленной частости 50%. Из этой точки на ось абсцисс опускают перпендикуляр и по шкале х определяют значение абсциссы этой точки. Эта величина и есть параметр х₀. Параметр σ представляет собой разность абсцисс точек, лежащих на прямой и имеющих ординаты 84,1 и 50%.

Как видно из рисунка, распределение образцов по проницаемости очень хорошо согласуется с найденным законом и, следовательно, с большой точностью может быть описано аналитически.

В таблице приведены значения параметров х₀ и σ по рассмотренным месторождениям и горизонтам. Здесь же сравниваются средние величины, средние квадратические отклонения и коэффициенты вариации проницаемости, определенные непосредственно по керну и по формулам, предлагаемым в настоящей статье. Как видно из таблицы, расхождение фактических и расчетных величин очень незначительно.

Следует оговориться, что по Туймазинскому месторождению в нашем распоряжении были фактические данные по керну с проницаемостью лишь выше 100 мд. По остальным месторождениям учитывались данные по проницаемости лишь выше 10 мд.

На практике часто бывает необходимо знать, в какой степени средняя величина проницаемости, определенная по нескольким десяткам образцов, соответствует истинной величине средней. Использовать для этого среднее квадратическое отклонение среднего арифметического нормального распределения нельзя из-за сильной асимметричности распределения проницаемости по керну. Однако найденная связь распределения проницаемости с нормальным законом позволяет решить эту задачу с позицией теории вероятности.

Известно [5], что выборочное среднее арифметическое из нормально распределенной совокупности само распределяется по нормальному закону с дисперсией σ²/n, а среднее квадратическое отклонение из такой совокупности распределяется асимптотически нормально с дисперсией σ²/2n, где n - количество определений. Таким образом, учитывая теорему о распределении суммы нормально распределенных величин и теоремы о дисперсии суммы и разности, можно считать, что величины х₀ + σ и х₀ - σ сами распределяются по закону, очень близкому к нормальному, со средним квадратическим отклонением

На основании этого с определенной степенью надежности можно установить верхнюю и нижнюю доверительные границы для среднего значения проницаемости, которые будут тем уже, чем больше произведено определений проницаемости. В качестве показателя надежности используется параметр t, который для количества образцов, не превышающих 100, необходимо брать из таблиц распределения Стьюдента, прилагаемых к руководствам по математической статистике.

Мерой надежности, наиболее часто применяемой в технике, является вероятность 0,95. В приложении к нашей задаче надежность 0,95 означает, что в 95 случаях из 100 средняя величина проницаемости, определенная по данному количеству образцов, отобранных случайно из различных участков пласта, более или менее равномерно расположенных по мощности и площади распространения, не выйдет за пределы установленных доверительных границ. Для уровня надежности 0,95 для 60 образцов показатель t = 2,0, для 40 образцов - 2,021 и для 20 образцов - 2,086.

Таким образом, в качестве верхней доверительной границы для среднего значения проницаемости, определенного по n образцам, с некоторой условностью можно считать величину:

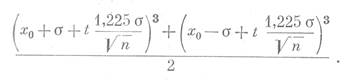
Нижней доверительной границей среднего значения проницаемости при том же количестве образцов п будет величина

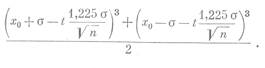
Несколько слов относительно критериев неоднородности эксплуатационного объекта по проницаемости. В настоящее время широкое распространение получило измерение неоднородности различных параметров пласта коэффициентом вариации. Однако этот коэффициент, как мера, изменяющаяся от нуля до бесконечности, несколько неудобен для оценки неоднородности пласта по проницаемости. Как известно, с неоднородностью по проницаемости связывают такие вопросы, как темп обводнения и коэффициент охвата пластов заводнением при вытеснении нефти водой. Для построения графиков, выражающих зависимость коэффициента охвата от степени неоднородности пласта по проницаемости, гораздо удобнее измерять эту неоднородность величиной, которая изменялась бы в интервале 0-1 и была соизмерима с коэффициентом вариации. В качестве такой величины можно ввести понятие коэффициента однородности пласта по проницаемости. Под коэффициентом однородности пласта по проницаемости предлагается понимать отношение медианного значения проницаемости к среднему арифметическому значению. Таким образом, при коэффициенте однородности, близком к нулю, будет иметь место очень резко выраженная неоднородность пласта по проницаемости, а при коэффициенте однородности, близком к единице, пласты будут сравнительно однородными по проницаемости.

Так, для рассмотренных в настоящей статье залежей коэффициент однородности горизонта Д_I по проницаемости изменяется от 0,72 до 0,85. Для горизонта Д_II тех же месторождений этот коэффициент более постоянен и колеблется от 0,87 до 0,88. Коэффициент однородности по проницаемости для горизонта С_I Мухановского месторождения равен 0,82. И, наконец, для бобриковского горизонта Арланского месторождения этот коэффициент равен 0,69. Еще более неоднородными по проницаемости являются песчано-алевролитовые отложения тульского горизонта Арланского месторождения, коэффициент вариации проницаемости которых составляет 190%. Коэффициент однородности в этом случае равен 0,24.

В заключение необходимо отметить, что для всех рассмотренных в настоящей статье совокупностей образцов графическим путем было проверено соответствие их распределению, предложенному М.М. Саттаровым. Во всех случаях получено хорошее совпадение и с этим распределением. Это наводит на мысль, что между параметрами распределения проницаемости, выведенными М.М. Саттаровым, и нормальным распределением существует если не функциональная, то очень тесная корреляционная связь.

ЛИТЕРАТУРА

1. Баишев Б.Т. Функции распределения проницаемости и учет неоднородности пласта при проектировании разработки нефтяных месторождений. Труды ВНИИ, вып. 28. Гостоптехиздат, 1960.

2. Дементьев Л.Ф. Методика определения кондиций для подсчета запасов нефти на примере горизонта одной из площадей Татарии. Труды ВНИИ, вып. 36 Гостоптехиздат, 1962.

3. Саттаров М.М. Применение методов математической статистики при определении коэффициента проницаемости нефтяного пласта. Труды УфНИИ, вып. 6, 1960.

4. Соломасов А.И. О точности определения проницаемости коллекторов по керну. Геология нефти и газа, 1962, № 8.

5. Смирнов Н.В. и Дунин-Барковский И.В. Краткий курс математической статистики для технических приложений. Физматгиз, 1959.

6. Пилатовский В.П. Замечания о некоторых применениях известных положений математической статистики при изучении распределения проницаемости пласта в данной совокупности наблюдений. Научно-технический сборник по добыче нефти, вып. 18, 1962.

7. Dykstra Н. and Parsons Н. L. The prediction of oil recovery by water flood. Secondary recovery of oil in the United States, 1950.

8. Law J. A statistical approach to the interstitial heterogeneity of sand reservoirs. Trans. AIME, vol. 155, 1944.

9. Muskat M. The effect of permeability stratification in complete water drive sistems. Trans. AIME, vol. 189, 1950.

ИГ и РГИ

Таблица

Месторождение, горизонт	Количество образцов	Параметры распределения			Среднее значение проницаемости, д		Относительное расхождение, %	Среднее квадратическое отклонение		Относительное расхождение, %	Коэффициент вариации, %		Относительное расхождение, %
		х0	σ	U=σ/х0	расчетное	по керну		расчетное	по керну		расчетный	по керну
Туймазинское, ДI	714	0,76	0,19	0,25	0,521	0,521	0	0,369	0,346	+6,23	70,8	66,4	+6,21
То же, ДII	1327	0,72	0,15	0,2083	0,422	0,418	+0,95	0,253	0,256	-1,86	59,9	61,3	-2,34
Константиновское, ДI	80	0,53	0,19	0,3584	0,206	0,212	-2,76	0,199	0,191	+3,87	96,3	90,1	+6,44
То же, ДII	288	0,58	0,13	0,2241	0,224	0,223	+0,67	0,144	0,143	+0,69	64,1	64,0	+0,16
Леонидовское, ДI	452	0,66	0,16	0,2424	0,338	0,338	0	0,233	0,218	+6,27	68,9	64,5	+6,39
То же, ДII	286	0,535	0,115	0,2149	0,174	0,172	+1,55	0,108	0,116	-7,80	61,7	67,5	-9,40
Татария *, ДI	1116	0,73	0,18	0,2466	0,460	0,453	+1,63	0,322	0,309	+3,89	69,9	68,4	+2,14
Мухановское, СI	419	0,925	0,25	0,2703	0,965	0,966	-0,09	0,732	0,734	-0,27	75,9	76,0	-0,13
Арланское, бобриковский	422	1,10	0,43	0,3909	1,941	1,941	0	2,006	1,895	+5,52	103,3	97,6	+5,52

* Данные о проницаемости керна этого месторождения заимствованы из работы [2].

Рисунок Распределение проницаемости в основных продуктивных горизонтах нефтяныхместорождений Урало-Поволжья.

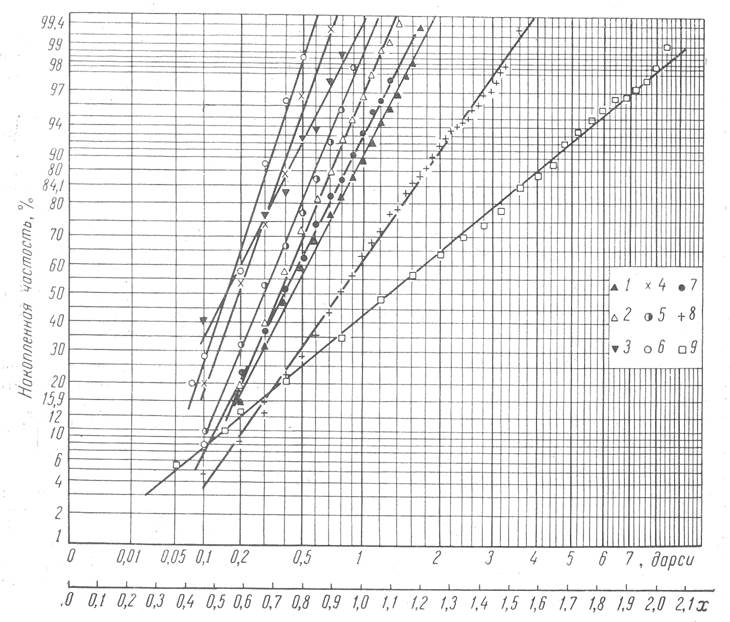
Месторождения: I - Туймазинское, Д_I, 2 - Туймазинское, Д_II, 3 и 4 - Конетантиновское, Д_I и Д_II; 5 и 6 - Леонидовское, Д_I и Д_II; 7 - одна из площадей Татарии, Д_I; 8 - Мухановское, C_I; 9 - Арланское, бобриковский горизонт.