К оглавлению

УДК 553.98:650.812.003.13

К методологии количественного прогнозирования эффективности поисково-разведочных работ на нефть и газ

И. X. АБРИКОСОВ, А. М. БЕЙЛИН (ВНИИОЭНГ)

Вопросам анализа и прогнозирования эффективности поисково-разведочных работ (ЭПРР) в последнее время уделяется большое внимание [2, 11]. Можно считать, что качественная сторона данного вопроса изучена достаточно полно. Исследованы основные факторы, оказывающие влияние на ЭПРР, выявлен и объяснен характер зависимости эффективности как функции от степени освоения начальных потенциальных ресурсов, накопленного объема поисково-разведочного бурения, собран и обобщен богатейший статистический материал.

Более скромными являются результаты, связанные с количественным прогнозированием ЭПРР, хотя именно эти прогнозы лежат в основе планирования прироста запасов, размещения объемов поисково-разведочного бурения и решения целого ряда других вопросов.

Важнейшим фактором, противодействующим высокоточному прогнозированию ЭПРР, является принципиально вероятностный и нестационарный характер этого показателя. Функциональные зависимости, которые обычно строят для определения ЭПРР [3, 6], при самом лучшем стечении обстоятельств могут быть лишь средними (точнее, математическими ожиданиями) действительной ЭПРР. Определенные резервы в повышении точности прогнозирования эффективности находятся в изучении недетерминированной составляющей ЭПРР, построении ее статистических характеристик.

Другим важным моментом, содержащим возможности повышения качества прогнозирования ЭПРР, является более тонкий учет системных факторов, сопутствующих данному прогнозу. В частности, при выборе моделей ЭПРР следует учитывать цели прогнозирования и его требуемую точность. Необходимо наличие ясности в вопросе должна ли используемая модель описывать некоторый конкретный нефтегазоносный район, его часть или же быть универсальной, т.е. пригодной для многих районов, комплексов. Кроме того, следует принимать во внимание уровень детальности доступной информации, ее качество, соизмерять объем трудозатрат, необходимых для прогнозирования эффективности по той или иной методике, с возможностями коллектива, решающего эту задачу, и установленными сроками.

Последнее означает возможность наличия одновременно нескольких типов моделей, различающихся по точности и сложности и имеющих каждая свои условия применимости. При этом важно, что множественность моделей может быть связана не с дифференциацией геологических особенностей, а с организационными и информационными проблемами, влияние которых на качество окончательных результатов не следует недооценивать. Правило, позволяющее отбраковывать заведомо неудачные модели, заключается в соблюдении принципа: более сложные модели должны быть и более точными, но не наоборот.

Ниже предлагается методика построения широкого класса моделей ЭПРР. Она позволяет формально получать целое семейство моделей, выбирая в качестве первоосновы лишь перечень основных факторов, подлежащих учету при прогнозировании ЭПРР. Многие известные модели ЭПРР [3, 6, 9] получаются при этом в качестве частных случаев. Метод позволяет получить и новые, перспективные для практических расчетов модели.

В дальнейшем рассматриваются лишь универсальные модели ЭПРР, предназначенные для проведения расчетов в большинстве нефтегазоносных районов. Модели такого типа должны удовлетворять определенным требованиям, а именно: они должны описывать наиболее экономичный режим распределения поисково-разведочных объемов бурения в рассматриваемом районе. В противном случае, распределяя разными способами одни и те же суммарные объемы бурения между участками района, мы получали бы различную результирующую эффективность в районе. Вторым требованием к универсальной модели ЭПРР является удовлетворительное качество работы и применимость в простейших, идеализированных ситуациях. Иначе на эту модель было бы трудно положиться в реальных, более сложных ситуациях. В качестве простейшего рассмотрим случай, когда нефтегазоносный район в достаточной мере однороден по геологической структуре и может быть разбит на несколько более мелких участков со сходными геологическими условиями, и эти участки имеют одинаковые характеристики ЭПРР.

Выбрав из тех или иных соображений факторы, входящие в модель ЭПРР, для описанного выше простейшего случая мы могли бы с помощью теории размерности [8, 10] построить максимально общий класс моделей, использующих эти факторы. Но тогда искомая модель также принадлежит этому классу. Далее, привлекая дополнительно качественный анализ эффективности в старых районах и статистические данные, из построенного класса для рассматриваемого района можно выделить единственную зависимость, являющуюся моделью ЭПРР. Такова логика построения моделей ЭПРР, примеры реализации которых приведены ниже.

Введем обозначения: v=v(t) -интенсивность поисково-разведочного бурения, т.е. число поисково-разведочных скважин, пробуренных в единицу времени, 1/год; Q = Q(t)-величина прироста запасов к моменту времени t, т; dQ/dt - скорость прироста запасов, т/год; - средняя величина запасов нефти (или газа) в одном месторождении района, т; Q₀ - начальные потенциальные запасы нефти (газа) в районе, т; n(t)-число поисково-разведочных скважин, пробуренных к моменту t,

Зависимость между скоростью прироста запасов, интенсивностью поисково-разведочных работ и геологическими характеристиками района будем искать в виде

где z= (z₁, ..., z_n) - некоторый набор показателей, в общем случае зависящих от времени, а- неизвестная функция своих аргументов, структуру которой предстоит уточнить. Наполняя вектор z тем или иным конкретным содержанием, можно получить разные классы моделей ЭПРР.

Используя принятые выше свойства универсальной модели ЭПРР и анализ размерностей [8, 10], можно существенно уточнить структуры функциональной зависимости (1). В наиболее интересных случаях имеющую место в выражении (1) неопределенность удается свести до безразмерной функции от единственной безразмерной переменной, причем качественное поведение этой функции известно.

Вернемся к рассмотренному выше простейшему случаю, когда идеализированный нефтегазоносный район может быть разбит на N совершенно одинаковых участков с одинаковыми начальными потенциальными ресурсами, одинаковыми интенсивностями поисково-разведочного бурения и другими одинаковыми усредненными геологоэкономическими характеристиками. Равенство расходуемых при этом на каждом участке объемов поисково-разведочного бурения следует из принятого ранее условия о наиболее экономичном расходовании ресурсов в районе. Тогда соотношение (1) для каждого участка может быть записано в виде

Заметим, что параметрне является суммируемым (аддитивным), поэтому он остается неизменным. Аналогично в векторе z выделены некоторые компоненты, являющиеся суммируемыми (экстенсивные факторы, z¹), а также несуммируемые компоненты (интенсивные факторы, z²).

Поскольку выражение (2) справедливо для любых N, то, взяв N-Qo, получим

где-некоторая неизвестная функция с числом аргументов на единицу меньше, чем у

Дальнейшее уточнение зависимости (3) можно получить, конкретизируя векторы параметров z¹ и z² и используя анализ размерностей. Напомним, что в основу метода анализа размерностей положен постулат, согласно которому правильные формулы остаются неизменными независимо от того, в каком масштабе измеряются входящие в них переменные. Следствием этого постулата являются формальные правила [8, 10], позволяющие уточнить функциональные зависимости между размерными переменными.

Рассмотрим примеры построения моделей ЭПРР.

1. Положим z¹ = Q, z² отсутствует. Тогда

Применяя анализ размерностей к формуле (4), получаем

где- некоторая безразмерная функция одного безразмерного аргумента. При этом в аргументы функции включены лишь те безразмерные величины, которые изменяются по мере проведения геологоразведочных работ.

Разделив обе части уравнения (5) на v(t) (там, где v(t)>0), с учетом получаем

Уравнение (6) - это уравнение для ЭПРР, измеренной в тоннах прироста запасов на одну скважину. Если ввести параметр- среднюю глубину одной скважины, то, разделив обе части, выражения (6) на и обозначив получим

Здесь ЭПРР измеряется уже в тоннах на метр бурения. Вводя стоимостные показатели 1 м бурения или одной скважины, можно аналогичным образом получить эффективность в тоннах на рубль вложенных затрат.

Нетрудно проверить, что формулы для ЭПРР, предложенные в работах [3, 6, 9], являются частными случаями выражения (7). Действительно, работе [6] соответствует

где А, В, С - некоторые безразмерные константы, работе [3]

а работе [9] для модели эффективности только разведочного бурения на открытых месторождениях соответствует

2. Положим z¹=n, z² отсутствует.

Тогда из формулы (3)

Применяя к этому уравнению анализ размерностей, получаем

или, по аналогии с проделанными выше преобразованиями,

где- некоторая безразмерная функция от одной безразмерной переменной.

3. Близкую к предыдущей модель можно получить, взяв- суммарный объем поисково-разведочного бурения, накопленный к моменту времени t, а- средняя глубина одной скважины. В конечном счете это приводит к модели эффективности вида

или

Частный случай таких моделей ЭПРР рассматривался в работе [1]. Заметим, что в общем случае необязательно равенствопоскольку в может быть включен объем опорного и параметрического бурения, а также скважин, бурение которых по тем или иным причинам прервано или не окончено.

4. В некоторых информационных ситуациях для прогнозирования ЭПРР может быть полезна модель, в которой z¹=S(t) (м²) - суммарная площадь месторождений нефтегазоносного района, получивших оценку поисково-разведочным бурением к моменту времени t в результате бурения n(t) скважин, z² отсутствует, а роль Q₀ играет S₀ - суммарная площадь всех месторождений нефтегазоносного района. В этом случае формула (3) будет иметь вид

В результате анализа размерностей после элементарных преобразований получаем модель эффективности вида

Конкретный вид зависимости связан с выбранной средней плотностью разведочного бурения на месторождениях и рядом других факторов.

Дальнейшее уточнение моделей ЭПРР связано с конкретизацией полученных функций(i= 1, 2, 3, 4).

Именно на данном этапе вступают в силу различного рода качественные соотношения и зависимости, аккумулирующие накопленные знания о поведении этого показателя. Действительно, в настоящее время широко распространена [1, 3, 6, 7] точка зрения, согласно которой показатель ЭПРР для достаточно однородных в отношении геологического строения нефтегазоносных районов ведет себя как унимодальная (имеющая один экстремум - максимум) функция от степени разведанности района. При этом с открытием первых месторождений, сопровождающимся существенным улучшением понимания геологического строения района, эффективность возрастает и достигает максимальных значений при освоении 15-25 % начальных потенциальных ресурсов (НПР) и в более редких случаях 35-40 %. Этот период сопровождается, как правило, открытием крупнейших месторождений. Затем эффективность снижается и устремляется к нулю по мере освоения НПР. Этот участок соответствует поздней стадии разведанности района.

Выбор конкретного вида функции (i=l, 2, 3, 4), обеспечивающих унимодальный характер ЭПРР, удовлетворительную аппроксимацию предыстории этих работ в районе и вместе с тем имеющих достаточно простую структуру, может быть предметом специального серьезного исследования. Современные методы решения такого рода задач достаточно подробно освещены в монографии [4].

В качестве первого приближения в задаче выбора конкретных функциональных зависимостейможно рекомендовать

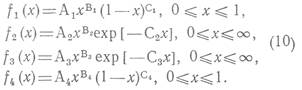
Тогда- константы, которые определяются по предыстории, например, по методу наименьших квадратов. К существенному облегчению численных расчетов может привести предварительное логарифмирование шкалы эффективностей и соответственно функций.

В случае, когда геологическое строение нефтегазоносного района существенно неоднородно или в различных его частях поисково-разведочные работы ведутся по различным методикам, то целесообразно район разбить на соответствующее число однородных участков и для каждого из них осуществить описанную выше процедуру. Для осуществления такого рода разделения района полезно понятие «направление геологоразведочных работ» [5].

Сравнивая выражение (10) с аналогичным соотношением (9), рекомендуемым в работе [3], можно видеть, что первое из них сложнее, поскольку в общем случае. Однако это обеспечивает значительно более гибкую настройку модели на предыстории. Модели (10) и (8), предложенные в работе [6], можно считать эквивалентными по сложности, поскольку они содержат одинаковое число свободных параметров, подлежащих настройке по фактическим данным. По-видимому, не существует серьезных аргументов в пользу одной модели. Заметим лишь, что некоторую неудовлетворенность оставляет наличие в модели (8) соотношения f₁(l)>0, т. е. последняя тонна НПР открывается с конечной, вполне осязаемой эффективностью.

В заключение заметим, что при настройке параметров в модели (6) или (7) независимо от конкретного выбора функции f1(х) может быть двоякое отношение к параметру Q₀ - НПР района. Этот параметр может быть либо рассчитан отдельно по одному из известных [7] методов, либо принят в качестве еще одного параметра, подлежащего определению статистическими методами по предыстории. На окончательный выбор оказать существенное влияние здесь могут различного рода информационные, ресурсные и организационные ограничения, с которыми сталкивается исследователь в процессе выполнения расчетов. Это же относится и к параметру S₀ - суммарной площади месторождений района в модели (4).

СПИСОК ЛИТЕРАТУРЫ

1. Баймухаметов К.С., Саттаров М.М. Об одной вероятностно-статистической модели прогнозирования прироста запасов. - Геология нефти и газа, 1975, № 3, с. 27-31.

2. Борисова A.И. Экономическая эффективность геолого-поисковых работ на нефть и газ. М., Недра, 1979.

3. Буялов Н.И., Корниенко В.Н., Лаврушкo И.П. Основы методики долгосрочного прогноза количества разведанных запасов нефти и газа. - Сов. геология, 1979, № 8, с. 3-13.

4. Вапник В.Н. Восстановление зависимостей по эмпирическим данным. М., Наука. 1979.

5. Крылов Н.А. О понятии «направление работ» при поисках нефтяных и газовых месторождений.- Геология нефти и газа, 1982, № 11, с. 17-22.

6. Методика прогнозирования эффективности поисково-разведочных работ на нефть и газ / Н.А. Еременко, Н.А. Крылов, Ю.С. Кувыкин, В.В. Стасенков. - Геология нефти и газа, 1979, № 1, с. 7-13.

7. Методы оценки перспектив нефтегазоносности. Под ред. Н.И. Буялова, В.Д. Наливкина. М., Недра, 1979.

8. Седов А.И. Методы подобия и размерности в механике. М., Наука, 1972.

9. Славкин В.С., Гильберштейн А.П., Пуркин Л. Б. Математическая модель зависимости эффективности разведочного бурения на нефть от удельной обеспеченности объемов разведочного бурения запасами категории С₂. - Геология нефти и газа, 1982, № 1, с. 57-59.

10. Хантли Г. Анализ размерностей. М., Мир, 1970.

11. Экономическая эффективность геологоразведочных работ на нефть и газ / Н.И. Бундов, В.М. Белокопытов, С.Я. Каганович и др. М., Недра, 1980.

Поступила 20/VI 1983 г.