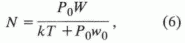
|
УДК 553.98.061.333 |
©А .Г. Арье, 1996 |
ГЕНЕРАЦИЯ И ПЕРВИЧНАЯ МИГРАЦИЯ УГЛЕВОДОРОДОВ В ГЛИНИСТЫХ НЕФТЕГАЗОМАТЕРИНСКИХ ТОЛЩАХ
А.Г
. Арье (ВНИГНИ)Проблема генерации и первичной миграции УВ – одна из важнейших в теории формирования залежей нефти и газа. Однако до настоящего времени она наиболее дискуссионна и наименее разработана (Белецкая С.Н., 1990). Хотя многие ее аспекты получили в той или иной мере однозначную трактовку, отсутствие целостной системы взглядов, логически исходящих из единых начальных представлений, создает впечатление фрагментарности ее познания.
Действительно, достаточно детально изучены такие параметры деструкции ОВ, как энергия активации, скорость прохождения реакций, влияние температурного режима, времени и т.д. Но за рамками исследования остался вопрос о роли пористой среды в такого рода реакциях.
Нет ясности и с механизмом вывода продуктов реакции в коллектор, несмотря на многочисленные предположения по этому поводу, включая такие экзотические, как растворение в сжатом газе или экспульсия. Все это не позволяет сконструировать достаточно понятную, физически непротиворечивую и логически последовательную модель процесса. А это в свою очередь приводит к тому, что проблема решается дискретно и как следствие лишь на качественном уровне.
Задача настоящей статьи состоит в том, чтобы показать возможность построения такой модели с помощью физически обоснованного расчетного аппарата для количественной оценки продуктивности нефтегазоматеринских толщ (НГМТ). Проблема оценки необходимых для расчета параметров на данном этапе разработки остается за рамками статьи.
В качестве исходной позиции принимается седиментационно-миграционная гипотеза происхождения природных УВ, согласно которой УВ-субстанция в стратисфере образуется за счет деструкции
РОВ, захороненного в НГМТ, причем процессы миграции рассматриваются в свете геофлюидодинамики медленных потоков [2].Природный процесс нефтегазообразования схематизируется в следующем виде. Нефтегазообразование происходит в терригенной толще, лишенной трещин. Генеральное направление естественного потока поровых флюидов – снизу вверх. Поток пересекает последовательно коллектор и покрышку. Источником формирования потока является отжатие флюидов из НГМТ.
УВ-вещество рассеяно по всему объему НГМТ, где, смешиваясь с поровыми водами, образует однородную молекулярную смесь ("пересыщенный раствор"). Количество образующегося УВ-вещества фиксируется на кровле глинистой НГМТ. Оценке подлежит только то количество УВ, которое поступило из НГМТ в коллектор. Коллектор (однородный песчаник
) согласно налегает на НГМТ и перекрывается глинистой покрышкой, непроницаемой для УВ-флюидов.Идеология решения в общих чертах сводится к следующему:
1. Образование УВ рассматривается как процесс, происходящий в поровом объеме НГМТ, заполненном седиментогенными поровыми водами.
2. Геометрические размеры каждой поры в глинистых породах НГМТ не позволяют образовавшимся УВ сформировать устойчивую границу раздела с поровой водой.
3. Скорость деструкции РОВ до момента предельного насыщения дериватами реакционного объема определяется скоростью разложения керогена, а впоследствии – скоростью удаления продуктов реакции из зоны их образования.
4. Продукты реакции выносятся через кровлю НГМТ по механизму молекулярно-дискретного движения жидкости в пористых средах в режиме файлюации при сокращении объема порового пространства НГМТ под действием литостатической нагрузки.
5. Молекулярная смесь УВ–поровая вода при переходе из НГМТ в пласт-коллектор разделяется на самостоятельные фазы, образуя УВ-эмулъсию в воде – конечный продукт первичной аккумуляции.
6. Молекулы воды, сопровождающие УВ в ходе первичной миграции, в соответствии с принципами геофлюидодинамики медленных потоков продолжают свой путь далее, пересекая отложения резервуара и покрышки. Первичные скопления УВ не могут выйти за пределы коллектора, так как наличие фазовой границы с водой перекрывающих коллектор флюидоупоров делает породы покрышки непреодолимым препятствием для таких скоплений [1].
7. Генеральный вектор миграции поровых вод как в НГМТ, так и в резервуаре имеет субвертикальное направление снизу вверх. Это не исключает возможность локальных латеральных перемещений, а в особых случаях и вертикальных – сверху вниз. Однако отмеченные отклонения от общей закономерности следует рассматривать как исключение. Иногда, особенно в отложениях резервуара, возможен и фильтрационный флюидообмен по обобщенному закону фильтрации.
8. Первичные скопления УВ формируются на границе резервуара с подстилающей его НГМТ, поэтому генерационной продуктивностью НГМТ следует считать величину
G, равную массовому количеству УВ, которое может выделяться на единичной площадке контакта резервуара с НГМТ.Часть выдвинутых идеологических позиций бесспорна по определению. Однако некоторые из них требуют дополнительных разъяснений. К их числу относится, например, соотношение между размерами каналов НГМТ и необходимым объемом первичного скопления УВ.
Усредненный диаметр каналов пористой среды
d несложно оценить с помощью широко известного отношенияd = 4n/S, (1)
где
n - пористость среды, доли единицы; S - удельная поверхность, м2 /м3.Глинистые НГМТ, как правило, характеризуются пористостью 10-20 %, а их удельная поверхность составляет не менее 10
8 м-1. Следовательно, диаметры поровых каналов глинистых НГМТ не превосходят в среднем 3 нм.Минимальный диаметр газового пузырька в водной среде может быть вычислен из следующих предпосылок:
1. Давление газа Р в таком пузырьке обусловлено действием двух составляющих: пластового давления Рг и давления силы поверхностного натяжения Рп, т.е.
Р=РП+РГ. (2)
Или в соответствии с законом Лапласа
Р = 2
где
s - коэффициент поверхностного натяжения жидкости, в которой образовался пузырек газа; r - радиус пузырька.2. Пузырьком газа можно считать такой ансамбль молекул УВ, масса которого равна или меньше выталкивающей силы, действующей на него в данной жидкости, что в формальной записи дает
NMg=rWg, (4)
где N -число молекул в ансамбле;
М -масса каждой молекулы; g -ускорение свободного падения; r -плотность жидкости; W -объем пузырька.3. Молекулярная энергия такого ансамбля, удерживающая пузырек от схлопывания (т.е. от растворения газа), определяется уравнением Ван-дер-Ваальса, в котором можно пренебречь силой межмолекулярного взаимодействия, так как газ практически не обладает внутренним давлением. В этом случае величина такой энергии, отнесенная к единице объема газового пузырька, равна давлению р
0 в этом пузырьке:Р
0 = NkT/(W -W0 ) (5)где Т - абсолютная температура газа, К;
k - постоянная Больцмана; W0 = Nw0; w0 = 12w - объем, приходящийся на одну молекулу газа при критических давлении и температуре; w - реальный объем одной молекулы газа.Из формулы (5) после несложных преобразований с учетом выражения для
w0 имеем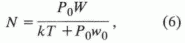
что после подстановки в равенство (4) дает
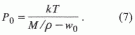
4. Условие всплывания пузырька обязательно предполагает наличие границы фаз, т.е. поверхности, ограничивающей объем пузырька. Необходимое и достаточное условие такой границы – равенство давлений в газовой и жидкостной фазах:
Р=-Р
0. (8)Подстановка значений давлений из (3) и (7) дает искомый диаметр пузырька в виде
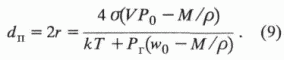
Расчет показывает, что при диаметре молекулы простейшего УВ-газа – метана, равном 0,38 нм,
w0 = 0,345 • 10-27 м3. Если при этом учесть, что М = 27,2·10-27 кг, r~ 103 кг/м3, k = 1,38·10-23 Дж/К, Т = 360 К, а s = 62,3·10-3 Н/м, то из формулы (9) легко определить значение минимального диаметра газового пузырька. При гидростатическом давлении нефтегазообразования Рг = 20 МПа оно составляет 7 нм. Это более чем вдвое превышает диаметр порового канала. Следовательно, в стесненных условиях порового пространства НГМТ образование газового пузырька невозможно, так как капиллярное давление в каналах диаметром 3 нм более чем в 5 раз выше давления Р0 при заданной температуре. Это нарушает необходимое условие существования газового пузырька в жидкости (8) и препятствует разделению фаз, так как внешнее давление приводит к схлопыванию пузырьков газа, т.е. к его "растворению" в поровой жидкости, если даже таковой и возникает.Понятно, что необходимое число молекул метана для образования пузырька равно
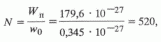
где
Wn - объем пузырька диаметром 7 нм.Минимальный диаметр пузырька нефти в водной среде рассчитывается исходя из приблизительно сходных соображений.
1. Пузырьком нефти в водной среде можно считать такой ансамбль ее молекул, который в состоянии образовать поверхность раздела жидких фаз. Приведенный (усредненный) радиус объема такого ансамбля можно получить из формулы (3):
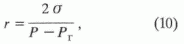
где
s - коэффициент пограничного натяжения в системе вода– нефть, равный приблизительно 45·10-3 Н/м; Р = Рг + р, где р - дополнительное молекулярное давление в уравнении Ван-дер-Ваальса, которое для жидкости при условии ее несжимаемости можно выразить из того же уравнения Ван-дер-Ваальса: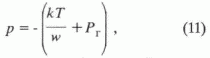
где
w - реальный объем одной молекулы жидкости, а знак "минус" связав с тем, что сила давления направлена к центру пузырька нефти.Тогда из (10) и (11) имеем окончательно
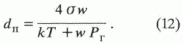
Полученная формула определяет минимальное значение диаметра пузырька нефти в водной среде. При этом реальный объем молекулы УВ с одним атомом углерода – метана, равный 0,287
·10-28 м3 , приблизительно в N раз меньше объема молекулы УВ, содержащей N атомов углерода. Отсюда для молекулы С12, характеризующей средний состав нефти [4], w ~ 3,5 ·10-28 м3.Нетрудно подсчитать с учетом данных, используемых для оценки размеров газовых пузырьков, что средний диаметр капелек первичной нефти не может быть меньше, чем 5.3 нм. Прямые измерения тонких дисперсий нефти в воде дают разброс этой величины 5-10 нм [4], что связано, вероятно, с различиями в размерах индивидуальных молекул нефти и степенью ее дисперсии.
Число молекул нефти в капле минимального размера составляет в среднем около 200. Как и в предыдущем случае, диаметр первичных капелек почти вдвое превышает диаметр поровых каналов НГМТ, а развиваемое в них капиллярное давление в 4 раза превышает "прочность" поверхности пузырька. Из этого следует, что образование так называемой микронефти в подавляющей части поровых каналов глинистых НГМТ оказывается невозможным.
Таким образом, согласно изложенному УВ-молекулы находятся в виде гомогенной смеси с молекулами поровой воды без разделения на фазы. Из этого следует, что они могут беспрепятственно перемещаться вместе с отжимаемыми поровыми водами в режиме файлюации.
Общая масса УВ, выносимая файлюационным потоком с единицы площади контакта НГМТ–породы резервуара, определяется как
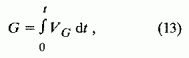
где
vg- скорость генерации УВ из ОВ НГМТ; t - время; G - генерационная продуктивность НГМТ.Образование УВ из РОВ можно рассматривать как элиминационный процесс, в котором исходной компонентой является реакционноспособная часть РОВ, а конечной продукцией – молекулы УВ. Тогда скорость реакции элиминации записывается известной формулой
V = e(Г-х)=eГе-et, (14) поскольку х = Г(е-et) [5].
В такой постановке
V – скорость образования УВ из РОВ; e – интегральная константа скорости реакции; Г– исходная концентрация реакционноспособной части РОВ в породе; х – масса УВ, сформировавшаяся за время t; e – основание натурального логарифма. Обычно e определяется экспериментально по скорости образования УВ из данного РОВ при разных температурах.Формула (14) справедлива для открытых систем, в которых продукты реакции беспрепятственно отводятся от очага реакции. В условиях пористой среды природных НГМТ с ограниченным поровым объемом в формулу (14) необходимо вводить множитель, учитывающий затрудненность отвода дериватов (продуктов реакции).
Поскольку, как было указано выше, в поровых каналах глинистых сред газ (или нефть) не может пребывать в виде самостоятельной фазы, реакция элиминации может продолжаться лишь до той поры, пока не исчерпается емкость перового пространства по отношению к УВ-веществу.
Величина такой емкости определяется растворимостью УВ в поровой воде при заданных давлении и температуре. Предельное значение концентрации дериватов в пластовых условиях выражает максимальную емкость реакционного объема. Скорость реакции с учетом этого обстоятельства лимитируется путем введения в (14) множителя
a = 1 – С/С0, где С – текущая концентрация УВ в поровой воде; c0 – ее максимально допустимое значение.Таким образом, скорость генерации УВ единицей площади поверхности кровли НГМТ составляет
(Собственно процесс генерации реализуется в НГМТ толщиной m, но вся продукция такой генерации проходит через поверхность контакта производящей толщи с коллектором. Поэтому объем генерации удобно нормировать площадью поверхности кровли НГМТ.)VG=emГ(1-С/С0)е-et, (15)
где
m - толщина НГМТ.Величина текущей концентрации УВ в потоке поровой воды, отжимающейся из НГМТ, по определению равна
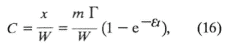
где
W - объем поровой воды, выделившейся в результате уплотнения НГМТ и/или прошедшей через нее за время t; х - масса произведенного УВ-вещества.Подставляя (15) и (16) в (13), будем иметь
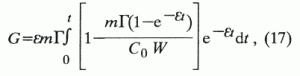
что после интегрирования и несложных преобразований дает
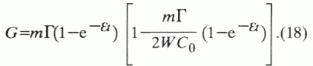
Согласно (15) полученная формула сохраняет справедливость пока С < С
0. При С = c0 генерация УВ прекращается. Если же текущая концентрация УВ превышает указанный предел, т.е. УВ-продукты деструкции начинают выделяться в самостоятельную фазу, образуя пузырьки газа или капельки нефти, то формула утрачивает физический смысл. Это дает основание разграничить процессы первичной и вторичной миграции УВ. К первичной миграции вслед за Н.А. Еременко, А.Э. Конторовичем, Ф.К. Салмановым и др. следует относить движение УВ-флюида в гомогенной смеси с поровой водой, а к вторичной – его движение в отдельной фазе, т.е. после образования пузырьков или капелек УВ.Таким образом, формула (18) справедлива в период первичной миграции УВ и утрачивает физический смысл при переходе к процессу вторичной миграции.
Из нее следует, что неравенство
G > 0 всегда выполняется. G = 0 при t = 0, а при t -” Ґ G стремится к G0 = mГ, что вполне реально.|
Поскольку W = w0 + Wф где Wф - объем файлюационного потока, проходящего через единицу площади НГМТ толщиной m, a w0 - объем поровой жидкости, заключенной в блоке НГМТ с единичным основанием и высотой m, значение mГ/2C0W всегда меньше 1. Действительно, w0 – объем, в котором происходит реакция деструкции РОВ. Он равен объему пустотного пространства НГМТ, включая объем, занимаемый РОВ. Это можно записать как W0=mn + mГ/r ,что в свою очередь позволяет утверждать, что неравенство
выполняется всегда, так как плотность РОВ не превышает 2 т/м 3 , а нередко оказывается существенно меньше; m/n > mГ в подавляющем большинстве случаев, представляющих практический интерес, и 2С0 на глубине нефтегазообразования всегда больше 1 кг/м3 . |
Как было обусловлено постановкой задачи, движение порового флюида в глинистых толщах в ненарушенных природных условиях на основании принципов геофлюидодинамики медленных потоков реализуется в режиме файлюации. При этом совершенно очевидно, что чужеродные поровой воде молекулы УВ-дериватов будут вынуждены попадать на ось порового канала с большей частотой, чем молекулы воды
(Это обусловлено тем, что вблизи стенок порового канала молекулы воды дополнительно связаны поверхностными силами минерального скелета, тогда как в центре канала равнодействующая этих сил равна нулю [1]. Приблизительно к такому же выводу приходит и P.A. Diskej (Possible Primary Migration of Oil from Source Rock in Oil Phase // Bull. AAPG. - 1975. - Vol. 59, № 2).). Поэтому концентрация УВ в файлюационном потоке оказывается большей, чем c0. Однако стерические условия порового пространства НГМТ, как указывалось, не позволяют таким молекулам объединиться в самостоятельную фазу. Вследствие этого они вынуждены мигрировать в гомогенной нестабильной смеси с молекулами поровой воды.На основании изложенного можно вычислить концентрацию УВ в файлюационном потоке, если их концентрация в объеме порового пространства равна С. Идеология такого расчета достаточно очевидна.
Если поровый канал радиусом
R и длиной l содержит N молекул растворителя, например воды, то можно записать, чтоpR2l = N 4/3pr3,
где
r - радиус молекул растворителя, из общего числа которых nt в фиксированный момент времени находятся на оси канала, т.е. постоянно имеют там вакантные места. Тогда l = 2rnt, что после подстановки в исходную формулу дает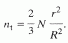
Другими словами, число молекул, попадающих одновременно на ось порового канала, в
R2/r2 раз меньше, чем две трети их общего числа N в канале. И поскольку частота попадания УВ-молекул на ось порового канала приоритетна по сравнению с молекулами воды, концентрация их в этой части порового пространства будет равна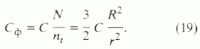
Полученная формула характеризует концентрацию УВ-вещества в файлюационном потоке
( Формула (19) справедлива для реакционных объемов, соразмерных с объемом, занимаемым молекулами дериватов, что характерно для порового пространства глинистых НГМТ.).Так, в поровом канале диаметром 3 нм, заполненном поровой водой с растворенным в ней УВ-веществом, концентрация его на оси канала будет в 150 раз больше, чем средняя по объему.
В то же время влияние отвода дериватов на процесс генерации начинается тогда, когда их концентрация приближается к
c0. Если значение последней составляет, например, 1 кг/м3 , то в файлюационном потоке оно станет равным уже 150 кг/м3 , что в условиях достаточного объема порового пространства невозможно, так как с неизбежностью приводит к выделению УВ-вещества в обособленную фазу.Из изложенного следует, что через единицу площади поверхности кровли глинистой НГМТ в коллектор выходит количество УВ, определяемое формулой (18). При этом процесс генерации тесно связан с первичной миграцией и во многом определяется ее интенсивностью.
Первичная миграция реализуется файлюационным потоком отжимаемых за счет литостатического давления поровых флюидов из НГМТ и залегающих ниже нее пород. Концентрация УВ-вещества в молекулярной смеси, образующей файлюационный поток в глинистых НГМТ, определяется формулой (19).
После выхода потока в коллектор стерические ограничения снимаются и избыток УВ-вещества образует каплю нефти или пузырек газа. С этого момента процесс первичной миграции прекращается. Образовавшаяся микрофаза УВ-вещества в дальнейшем мигрирует самостоятельно, используя поровую воду как среду для движения. Потенциалом вторичной миграции служат выталкивающая сила в соответствии с законом Архимеда, а также силы взаимодействия на границах УВ-фазы и воды.
Миграционное пространство УВ-фазы ограничивается областью распространения коллектора как в латеральном направлении, так и по вертикали. На контакте УВ-скопления с перекрывающей коллектор малопроницаемой толщей возникает сила капиллярного давления, направленная против силы всплывания, и если эта сила оказывается больше, чем сила всплывания, такую толщу можно называть покрышкой. Проницаемость ее должна удовлетворять неравенству

Если неравенство (20) выполняется, УВ-скопление не в состоянии преодолеть сопротивление покрышки. Однако это не относится к воде, пришедшей в коллектор вместе с УВ-молекулами в файлюационном потоке. Для нее покрышка проницаема. Это связано с тем, что поровое пространство покрышки также заполнено водой. Следовательно, вода, пришедшая в коллектор, в файлюационном режиме легко проходит покрышку на участках отсутствия фазовых границ между флюидами. Действительно, отсутствие фазовой границы между водой коллектора и покрышки эквивалентно утверждению о том, что на их контакте
s=0. Подстановка этого значения в неравенство (20) показывает, что файлюационное течение через покрышку невозможно только в том случае, если Кп = 0. А это для реальных пористых сред (в том числе и глин) недостижимо.Следует особо отметить, что покрышка становится файлюационно непроницаемой для поровой воды коллектора на участках прямого контакта покрышки с УВ-фазой. Это также следует из формулы (20) и широко известно под названием эффекта Жамена.
Таким образом, вода файлюационного потока выполняет транспортную функцию для молекул УВ в процессе первичной миграции и, сбрасывая излишек этих молекул в коллекторе, продолжает свое движение через покрышку, тогда как образовавшаяся УВ-масса накапливается в коллекторе и коалесцирует. В этом процессе, который следует называть вторичной миграцией, микроскопления УВ перемещаются самостоятельно, используя поровую воду коллектора как миграционную среду.
Приведем пример оценки генерационной продуктивности НГМТ. Необходимый набор параметров для этого включает: толщину НГМТ, толщину подстилающих ее пород, подвергающихся заметному уплотнению за время
t от начала генерации, коэффициент скорости деструкции РОВ, предельную растворимость УВ в поровой воде и, наконец, продолжительность процесса деструкции РОВ.Предположим, что деструкция реализуется в течение 50 млн лет
при температуре 373 К, за это время сжимаемая толща пород уплотнится на 10 % абсолютного значения пористости (например, от 20 до 10 %), толщина уплотнившегося пласта, включая НГМТ, равна 100 м, а толщина НГМТ – 30 м. Предельная растворимость УВ в пластовой воде не более 6 кг/м3 (для метана), средняя энергия активации реакции деструкции РОВ составляет 200 кДж/моль, а предэкспоненциальный множитель А = 3,15·1020 1/год.Из известного уравнения Аррениуса коэффициент скорости реакции деструкции равен:
e
=А е-E/RT, (21)где Е - энергия активации деструкции;
R - универсальная газовая постоянная; Т - абсолютная температура системы.Подставляя предложенные значения в формулу (21), получим, что
e ~ 2,8·10-8 1/год. И тогда, при условии, что W = 10 м3/м2, а Г = 0,1 % = 2,3 кг/м3, после подстановки этих и других названных параметров в формулу (18) получим, что через 50 млн лет после вхождения НГМТ в фазу активного нефтегазообразования она может произвести массу УВ, равную 26·103 т/км2, т.е. G = 26·103 т/км2.Полученная величина хорошо согласуется в результатами балансовой оценки, проведенной в детально изученных районах [3].
Таким образом, совместное использование принципов геофлюидодинамики медленных потоков и законов химической кинетики позволило впервые разработать физически непротиворечивую модель генерации и эмиграции УВ в глинистых НГМТ, а также получить аналитические выражения для количественной оценки процесса на каждом из этапов, включая интегральную оценку продуктивности НГМТ.
Проведенный анализ позволяет утверждать, что:
1. Генерация УВ в глинистых НГМТ происходит путем деструкции молекул
РОВ в соответствии с законами химической кинетики.2. Скорость генерации зависит не только от температуры системы и времени, но и от интенсивности файлюационного движения поровой воды (как самой НГМТ, так и поступающей из подстилающих ее пластов). С уменьшением интенсивности потока генерация замедляется.
3. Миграция УВ-дериватов реализуется в режиме файлюационного течения смеси молекул воды и УВ-вещества. Концентрация последних многократно превышает допустимую для воды вне порового пространства.
4. Главным направлением первичной миграции УВ-дериватов является вертикальное – снизу вверх.
5. Покрышка удерживает УВ-скопления в коллекторе за счет сил Лапласа, возникающих на границе фаз при попытке УВ-фазы внедриться в нее.
6. Расчет генерационной продуктивности глинистых НГМТ по формуле (18) дает результаты, вполне сопоставимые с балансовыми оценками в детально изученных районах.
Приведенные решения удовлетворяют заданным модельным условиям. Их необходимо учитывать при рассмотрении реальной геологической ситуации. Ее следует схематизировать, т.е. привести к модельному виду, аналогичному тому, который применялся при выводе формулы. При этом необходимо с максимально возможной детальностью учитывать особенности реальной модели и проводить анализ каждого ее упрощения в отношении влияния последнего на погрешность конечного результата расчета.
ЛИТЕРАТУРА
The problem is for the first time regarded on the basis of chemical kinetics of organic matter destruction taking into consideration the influence of porous water movement on the intensity of reaction itself. Generation and washing out of hydrocarbons from source rocks are thought to be as a single process. Such approach to this problem is first realized on the basis of geofluidodynamics of slow flows (GSF). It was shown that generation intensity depends not only on temperature and time but on porous water movement intensity too. In accordance with the GSF laws, emigration of hydrocarbons generating from source rocks is realized in molecular-discrete form upwards. Due to restricted size of the porous space in shales, the hydrocarbon molecules are unable to appear in a separate phase despite of the fact that the hydrocarbon molecules concentration in their mixture with porous water molecules greatly exceeds concentration admissible for solutions. Molecular mixture moves in such state until it enters the first reservoir where an independent hydrocarbon phase is originated due to steric limitations removal. The equations for source rocks productivity calculation are given along with comparison of results obtained with these equations and data of empirical estimations. It was shown that the calculation error is quite permissible for such type of estimations.